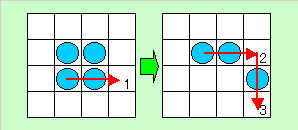
◆広島県 清川 育男 さんからの解答
【問題1】
(2,3)→(2,1),(2,4)→(2,6),(3,3)→(3,1),(2,1)→(4,1),
(3,4)→(3,6),(2,6)→(4,6),(4,2)→(6,2),(5,4)→(5,2),
(5,5)→(3,5),(4,3)→(4,5),(4,6)→(4,4),(6,2)→(4,2),
(4,1)→(4,3),(4,3)→(4,5),(3,5)→(5,5)
【問題2】
(2,3)→(2,1),(2,5)→(2,7),(4,2)→(2,2),(2,1)→(2,3),
(4,6)→(2,6),(2,7)→(2,5),(4,4)→(4,6),(6,4)→(4,4),
(5,6)→(5,4),(4,3)→(4,5),(4,6)→(4,4),(6,6)→(6,4),
(2,3)→(4,3),(2,5)→(4,5),(6,2)→(4,2),(4,3)→(4,1),
(4,5)→(4,3),(2,4)→(4,4),(4,4)→(4,2),(4,1)→(4,3),
(6,4)→(6,2),(4,3)→(6,3),(6,2)→(6,4),(6,4)→(4,4)
【問題3】
マスを3色で塗り分ける。
6) 12 12 12 不可能。
【おまけ】
Nが3の倍数のとき不可能。
下のプログラムによる結果
REM 3色に塗り分けてその個数を数える。
REM 3色が同数個の場合は不可能
DIM A(101) !N=50まで
DIM B(3)
DIM G$(2)
LET G$(1)=" 可能"
LET G$(2)=" 不可能"
FOR N=1 TO 50
PRINT USING "###":N;
PRINT ")";
FOR I=1 TO 3
LET B(I)=0
NEXT I
LET Z=0
FOR I=1 TO N
LET Z=Z+1
LET A(Z)=I
NEXT I
FOR I=N-1 TO 1 STEP -1
LET Z=Z+1
LET A(Z)=I
NEXT I
FOR I=1 TO 2*N+1
LET R=REMAINDER(I,3)
IF R=0 THEN
LET R=3
END IF
LET B(R)=B(R)+A(I)
NEXT I
FOR I=1 TO 3
PRINT USING "####":B(I);
NEXT I
IF B(1)=B(2) AND B(2)=B(3) THEN
LET F=2
ELSE
LET F=1
END IF
PRINT G$(F)
PRINT
NEXT N
END◆愛知県 Y.M.Ojisan さんからの解答
【おまけ解答】
【補題1】
n=1 の時は初めから成立しており可能である。
【補題2】
n=2 の時は下図の手順で可能である。

【補題3】
n=3m のとき 第140回の解答方法により分類すると、
各3グループの数は全て 3m2で同一であり、偶奇性が一致して不可能である。
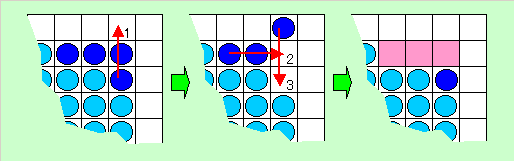
【補題4】
下図に示すように、角の「曲がり4目」の配置はそのうちの「直列に並ぶ3個」を消去することが可能である。
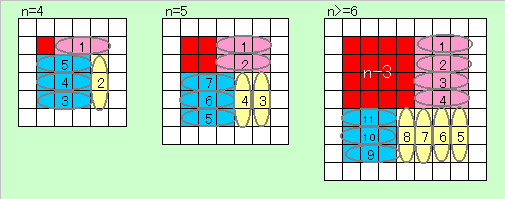
【補題5】
下図に示すように、補題4を用いて一辺n個(n>3)の問題を
一辺n−3個の問題に十分条件として変換可能である。
【おまけ1】
nが3の倍数でないとき可能。
∵ nが3の倍数ではないとき、補題5の反復により、n=1または2の問題に変換できる。
補題1,2よりn=1,2は可能である。
よって、解答となる。
【おまけ2】
補題5の手順を繰り替えし、n=1または2の状態にする。
n=2になる場合は最後に補題2の手順を適用する。
【おまけ3】
∵ 補題3よりnが3の倍数のときは不可能である。
◆千葉県 なのはな子 さんからの解答
【問題1】
(3,3)→(1,3),(2,5)→(2,3),(5,3)→(3,3),(5,5)→(5,3), (2,3)→(4,3),(4,4)→(2,4),(4,5)→(2,5),(2,5)→(2,3), (1,3)→(3,3),(4,2)→(4,4),(5,2)→(5,4),(5,4)→(3,4), (2,2)→(4,2),(3,4)→(3,2),(4,2)→(2,2) (3,5)→(1,5),(2,3)→(2,5),(1,5)→(3,5),(4,3)→(2,3), (2,2)→(2,4),(4,5)→(4,3),(2,4)→(4,4),(5,3)→(3,3), (3,2)→(3,4),(3,5)→(3,3),(5,5)→(5,3),(5,2)→(3,2), (3,2)→(3,4),(3,4)→(5,4),(5,4)→(5,2)【問題2】
(5,2)→(7,2),(5,3)→(7,3),(7,2)→(7,4),(3,3)→(5,3), (4,5)→(4,3),(4,2)→(4,4),(2,2)→(4,2),(5,4)→(5,2), (5,2)→(3,2),(3,5)→(3,3),(3,2)→(3,4),(7,4)→(5,4), (6,5)→(4,5),(3,4)→(1,4),(2,6)→(2,4),(1,4)→(3,4), (4,4)→(2,4),(4,6)→(4,4),(6,6)→(4,6),(4,6)→(2,6), (2,3)→(2,5),(2,6)→(2,4),(5,4)→(3,4),(3,4)→(1,4) (5,2)→(7,2),(5,4)→(5,2),(4,2)→(6,2),(2,2)→(4,2), (3,4)→(5,4),(5,5)→(5,3),(3,5)→(5,5),(4,2)→(4,4), (2,3)→(4,3),(4,3)→(4,5),(4,6)→(4,4),(2,6)→(4,6), (5,6)→(3,6),(2,4)→(2,6),(2,6)→(4,6),(6,5)→(4,5), (6,3)→(6,5),(6,6)→(6,4),(7,2)→(5,2),(5,2)→(5,4), (4,5)→(4,3),(6,4)→(4,4),(4,3)→(4,5),(4,6)→(4,4) (3,4)→(1,4),(2,6)→(2,4),(5,4)→(3,4),(5,6)→(5,4), (6,4)→(4,4),(6,6)→(6,4),(2,3)→(2,5),(4,4)→(2,4), (4,6)→(4,4),(3,6)→(3,4),(3,4)→(5,4),(6,4)→(4,4), (6,2)→(6,4),(5,2)→(5,4),(5,4)→(3,4),(4,2)→(4,4), (3,4)→(5,4),(6,4)→(4,4),(2,5)→(2,3),(2,2)→(2,4), (1,4)→(3,4),(4,4)→(2,4),(3,2)→(3,4),(2,4)→(4,4) (3,6)→(1,6),(3,5)→(1,5),(1,6)→(1,4),(3,3)→(3,5), (5,4)→(3,4),(5,6)→(5,4),(6,4)→(4,4),(6,6)→(6,4), (3,4)→(5,4),(1,4)→(3,4),(3,5)→(3,3),(4,6)→(4,4), (5,4)→(3,4),(2,2)→(2,4),(2,4)→(4,4),(3,2)→(3,4), (3,4)→(5,4),(6,4)→(4,4),(4,3)→(4,5),(6,3)→(4,3), (4,2)→(4,4),(4,5)→(4,3),(6,2)→(4,2),(4,2)→(4,4)【問題3】
存在しません。
【おまけ1】
nがn≧2で3の倍数以外の場合、最後に石が一つだけ残るような手順が存在する。
【おまけ2】
n=2の場合、上下・左右に各1行・1列のマス目があるとして、
(2,3)→(4,3),(2,2)→(4,2),(4,3)→(4,1)
n=4、n=5の場合は、【問題1】【問題2】の解答のとおり。
(n≧7以上の場合については省略。)
【おまけ3】
nが3の倍数の場合、1手ごとに
(奇・奇・奇)→(偶・偶・偶)→(奇・奇・奇)→(偶・偶・偶)→…をくり返すことになるので、最後に1つだけ石を残すことは不可能です。
◆宮城県 アンパンマン さんからの解答
【問題1】
(3,4)→(3,6),(5,5)→(3,5),(3,6)→(3,4),(3,3)→(1,3),
(2,5)→(2,3),(1,3)→(3,3),(3,2)→(1,2),(3,4)→(3,2),
(4,2)→(2,2),(1,2)→(3,2),(4,4)→(4,2),(4,2)→(6,2),
(5,4)→(5,2),(6,2)→(4,2),(4,2)→(2,2)
最後のマス目は(2,2),(2,5),(5,2),(5,5)しかありません。
理由はおまけ3)に示されています。
【問題2】
(3,3)→(3,1),(5,2)→(3,2),(2,2)→(4,2),(5,3)→(3,3),
(3,4)→(3,2),(3,1)→(3,3),(2,3)→(4,3),(5,4)→(3,4),
(4,2)→(4,4),(5,6)→(7,6),(6,4)→(6,6),(6,2)→(6,4),
(7,6)→(5,6),(5,6)→(5,4),(4,5)→(4,3),(6,4)→(4,4),
(4,3)→(4,5),(3,6)→(1,6),(2,4)→(2,6),(1,6)→(3,6),
(4,5)→(2,5),(4,6)→(2,6),(2,6)→(2,4),(2,4)→(4,4)
最後のマス目は(4,4)しかありません。
理由はおまけ3)に書いてあります。
【問題3】
存在しません。
【おまけ1】
3で割り切れないnです。
【おまけ2】
X ABC DのようにAB,C,Dは石があって,Xのところが石がないとするとD,A,Xという順番で動かすと最後に石がD のところに一個しか残りません。
n=3m+1の場合、
例としてn=7を考えてみると
XXXXX XHHHO XDEFO XDEFO XDEFO XABCO XABCO XABCO XXXXX3個ずつのA,D,B,E,H,C,Fという順番で石を消すと3*nの石がなくなります。
n=3m+2の場合、
例としてn=8を考えてみると
XXXXX XGGGO XHHHO XDEFO XDEFO XDEFO XABCO XABCO XABCO XXXXX3個ずつのA,D,B,E,G,H,C,Fという順番で石を消すと3*nの石がなくなります。
【おまけ3】
ABC CAB BCAのようにつけると
n*nの場合は
Aの数
| =n+2{(n-3)+(n-6)+...+(n-3[ | n 3 | ])} |
| =n+2n[ | n 3 | ]-3[ | n 3 | ] | [ | n+3 3 | ] |
| =n+(2n-3-3[ | n 3 | ])[ | n 3 | ] |
BとCの数は同じで
| ={n2 | -{n+(2n-3-3[ | n 3 | ])[ | n 3 | ]}}/2 |
| ={n2 | -n-(2n-3-3[ | n 3 | ])[ | n 3 | ]}/2 |
nが3で割り切れる場合、n=3m。
| このときA,B、Cの数は同じで=3m2= | n2 3 | 。 |
奇遇を考慮して一個の石が残るような手順が存在しないことが分かります。
nが3で割り切れない場合、
| このときAの数は= | n2+2 3 | , |
| BとCの数は同じで= | n2-1 3 | 。 |
つまりAの数はBとCの数より一個多いことが分かります。
つまり手順が存在する可能性があります。
最後に一個残る方法はおまけ2)に示されています。
また対称性を考慮すると、最後の一個の可能なマス目は二つのケースに考えられます。
一番左上を(1,1)とすると
nが奇数の場合、
| ( | n+3 2 | +3r, | n+3 2 | +3s); r,s=-[ | n-1 6 | ],-[ | n-1 6 | ]+1,...,0,...,[ | n-1 6 | ] |
| 合計= | (1+2[ | n-1 6 | ]) | 2 |
nが偶数の場合、
| ( | n 2 | +3r, | n 2 | +3s); r,s=-[ | n-4 6 | ],-[ | n-4 6 | ]+1,...,0,...,[ | n+2 6 | ] |
| 合計= | (2[ | n+2 6 | ]) | 2 | , n>3 |
◆京都府 sanza さんからの解答
【問題1】
(3,2)→(1,2),(2,4)→(2,2),(1,2)→(3,2),(4,4)→(4,6),
(2,5)→(4,5),(4,6)→(4,4),(4,3)→(6,3),(5,5)→(5,3),
(6,3)→(4,3),(3,3)→(3,1),(5,2)→(3,2),(3,1)→(3,3),
(4,3)→(2,3),(4,4)→(2,4),(2,4)→(2,2)
【問題2】
(3,2)→(1,2),(2,4)→(2,2),(1,2)→(3,2),(4,3)→(4,1),
(6,2)→(4,2),(4,1)→(4,3),(5,4)→(7,4),(6,6)→(6,4),
(7,4)→(5,4),(2,5)→(2,7),(4,6)→(2,6),(2,7)→(2,5),
(4,4)→(4,2),(6,3)→(4,3),(4,2)→(4,4),(4,4)→(6,4),
(5,6)→(5,4),(6,4)→(4,4),(4,4)→(4,6),(2,5)→(4,5),
(4,6)→(4,4),(4,4)→(2,4),(3,2)→(3,4),(2,4)→(4,4)
【問題3】
無理っス。
【おまけ1】
nが3の倍数以外のとき。
(n=3k+1、3k+2のとき)(kは0以上の整数)
【おまけ2】
=前提=
1、2×2の石は、
● ●● ○● ●● → ●○ → ○○ → ○○ ●● ●のように1個にすることができる。
2、3×3の石は、絶対に一個にはできない。
初手は、
1、真ん中の石を動かす。
2、辺の石を動かす。
の2通りしかない。
● ●● ●○ ● 1、 ●●● ●○● ● ○ ● ● ○ ●●● → ● ● → ● → ● → → ● → ● ●●● ●●● ●●● ●●● ○●● ●● ●○ ● ● ● 2、 ●●● ● ○● ● ●● ●●○ ○● ●● ●○ ●●● → ●●● → ●●○ → ●● → ●● → ●○ → ● ●●● ●●● ●● ●● ●● ● ●他の道筋もあるが、いずれにせよ絶対に一個にはできない。
3、連なった3つの石は、絶対に一個にはできない。
●●● と ●● ●
石がくっついている必要があるので、外から消していくのが自然なやり方です。
効率よく消す方法が下記の手順。
この方法で、3つの石を消すことができます。
● ● ●●●● → ●●○● → ○●● → ○● ●●●● ●● ● ●● ● ●●●●のように石を消す事ができます。
まず、一辺が n=3k+1 の正方形を考えます。
この外周を上記の方法で取り除いていくと、一辺が n=3k−1 の正方形になります。
●●●●・・・●●●● ● ● ●●●・・・●●● ● ● ● ● ● ● ● ● ・ ・ ・ ・ ・ ・ → ・ ・ ・ ・ ・ ・ ● ● ● ● ● ● ● ● ● ● ●●●・・・●●● ●●●●・・・●●●●この正方形の外周をさらに取り除きます。
●●●・・・●●● ● ● ● ●●●・・・●● ● ● ● ● ・ ・ ・ ・ ・ ・ → ・ ・ ・ ・ ・ ・ ● ● ● ● ● ● ●●・・・●●● ●●●・・・●●● ●この正方形もどきからさらに外周を取り除くと、
● ●●●・・・●● ● ● ●・・・● ・ ・ ・ ・ ・ ・ → ・ ・ ・ ・ ・ ・ ● ● ●・・・● ●●・・・●●● ●よって
同様に、
k=4 のとき、 n=13、n=11 から n=7 へ
k=5 のとき、 n=16、n=14 から n=10 へ
サイズを小さくすることが可能です。
ここに周期性が見られます。
よってn=1は自明。n=2は証明済み。n=3は不可
n≧4において、 n=3k+1、3k+2(kは1以上の整数)ならば題意に適する。
よって、
n=3k+1、3k+2(kは0以上の整数)
証明終わり
◆神奈川県 ヘリトンボ さんからの解答
【問題1】
(4,4)→(4,6),(2,5)→(4,5),(4,6)→(4,4),(4,3)→(4,5),
(5,5)→(3,5),(2,3)→(4,3),(3,5)→(3,3),(4,2)→(4,4),
(5,4)→(3,4),(2,4)→(4,4),(2,2)→(4,2),(5,2)→(5,4),
(5,4)→(3,4),(3,4)→(3,2),(3,2)→(5,2)
【問題2】
(4,5)→(4,7),(2,6)→(4,6),(6,5)→(4,5),(5,6)→(3,6),
(6,3)→(6,5),(6,6)→(6,4),(4,4)→(4,6),(4,7)→(4,5),
(3,5)→(5,5),(3,3)→(3,5),(3,6)→(3,4),(6,4)→(4,4),
(5,2)→(5,4),(5,5)→(5,3),(3,2)→(5,2),(6,2)→(4,2),
(5,3)→(3,3),(2,3)→(4,3),(2,5)→(2,3),(2,2)→(2,4),
(3,4)→(5,4),(4,2)→(4,4),(5,4)→(3,4),(2,4)→(4,4)
【おまけ1】
nが3の倍数でないとき
【おまけ3】
盤面のマスにa・b・cの3種類の文字を縦横に規則正しく順番につけていく。
例えば、6×6の盤面であれば次のように文字を配置する。
abcabc bcabca cabcab abcabc bcabca cabcab無限の広さを持つ盤面にもこのように文字をつけていく。
最初、a・b・cそれぞれのマスにある石が同数の場合、上記より、何回操作を行ってもa・b・cにある石の総数の差は偶数となるため、最後に石が1つ残るという状態をつくることはできない。
nが3の倍数のとき、a・b・cそれぞれに配置されている石の個数は等しくなるので、すなわち、nが3の倍数のとき、最後に石が1つだけ残るような手順は存在しない。
◆ 問題へもどる
◆ 今週の問題へ