
【コメント】
【おまけの問題】の不可能な場所を見つけるきれいな方法があります。
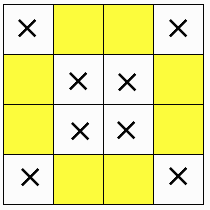
最初にマス目を図のように3色に塗り分けます。

初期状態では緑色のマス目に6個、赤色のマス目に5個、水色のマス目に5個の石があります。
3色のマス目に入っている石の数を(6,5,5)のように表します。
ある石が他の石を飛び越して1個減るとき、2つの色のマス目については石が一つ減り、1つの色のマス目については石が一つ増えます。
つまり1手ごとに、3色のマス目に入っている石の数の偶奇は、3色とも変わることになります。
例えば緑色のマス目の石を最初に1個取ってはじめると
最初は(5,5,5)つまり3色とも奇数個ですから、何回飛び越しても
(偶,偶,偶)または(奇,奇,奇)にしかなりません。
ですから1個だけ残った状態の
(1,0,0)、(0,1,0)、(0,0,1)のどの状態にすることも不可能です。
以上のことから図の緑色のマス目の石を1個取ってはじめると、最後に1個のみを残すことは不可能です。
あとは対称性を考慮して、図の×じるしの8ヶ所から最初に取ると不可能であることがわかります。
問題1のように赤色の石を1個取ってはじめると、
スタートは(6,4,5)ですからうまい手順を考えれば
(0,0,1)とできる可能性があります。
実際にやってみると、×じるしの8ヶ所以外のマス目(黄色のマス目)から1個取ってはじめると可能であることがわかります。
◆広島県 清川 育男 さんからの解答
(1,4)→(1,2),(1,1)→(1,3),(3,4)→(1,4),(2,2)→(2,4),
(1,4)→(3,4),(4,2)→(2,2),(2,1)→(2,3),(3,4)→(3,2),
(1,3)→(3,3),(4,4)→(4,2),(4,1)→(2,1),(4,2)→(2,2),
(2,1)→(2,3),(3,3)→(1,3)
【おまけ1】
1 可能 0 不可能 ( 1 , 1 ) 0
( 1 , 2 ) 1
( 1 , 3 ) 1
( 1 , 4 ) 0
( 2 , 1 ) 1
( 2 , 2 ) 0
( 2 , 3 ) 0
( 2 , 4 ) 1
( 3 , 1 ) 1
( 3 , 2 ) 0
( 3 , 3 ) 0
( 3 , 4 ) 1
( 4 , 1 ) 0
( 4 , 2 ) 1
( 4 , 3 ) 1
( 4 , 4 ) 0
◆千葉県 TKWT さんからの解答
【問題】 14手
(1,4)→(1,2) (3,4)→(1,4) (1,1)→(1,3) (1,4)→(1,2)
(3,1)→(1,1) (1,1)→(1,3) (2,3)→(2,1) (4,2)→(2,2)
(4,4)→(4,2) (4,1)→(4,3) (4,3)→(2,3) (1,3)→(3,3)
(2,1)→(2,3) (2,3)→(4,3)
【おまけ1】
計8ヶ所
A:4個の隅...(1,1)(1,4)(4,1)(4,4)
B:中央部の4個...(2,2)(2,3)(3,2)(3,3)
◆ 問題へもどる
◆ 今週の問題へ