
◆山梨県 Footmark さんからの解答
問4,問5,問6は、最少手数の解が5通りあります。

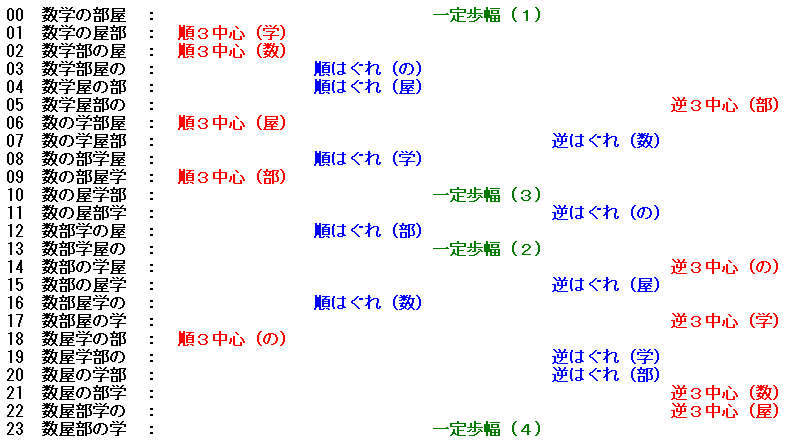
なお、『5文字の置き替え』問題を、『5組の夫婦』の解答風に表現すると以下になります。
◆千葉県 なのはな子 さんからの解答
【問題1】 屋1
【問題2】 部2
【問題3】 部1→の1
【問題4】 数2→の1
【問題5】 学1→数2
【問題6】 学2→屋1→数1
◆宮城県 アンパンマン さんからの解答
数=1,学=3,の=5,部=2,屋=4と定義すると
動かす前のパターンは1-3-5-2-4 (五角形の頂点の時計回り)
このパターンは12345(星形の頂点の時計回り)のパターンの一対一の関係です。
元のパターンの示し方を1-3-5-2-4とし、変形したパターンの示し方を12345とします。
各操作の最後の手順(数が上にくるようにすること)は順番に影響ないし、回転されても同じパターンと考えます。
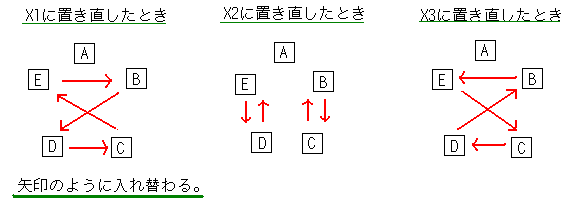
XYZWUのパターンを考えます。
操作X(1)はXとUの置き換え操作になります。→(XUYZW)
つまりXと左側の隣の文字と置き換えることです。
操作X(2)はXとWとUの一回逆時計回り回転操作になります。→(XWUYZ)
(Xを反対の辺にいれると同じ)
(=操作X(1)X(1)または 操作X(3)X(3))
操作X(3)はXとYの置き換え操作になります。→(XZWUY)
つまりXと右側の隣の文字と置き換えることです。
(=操作Y(1))
【問題1】
12345→13245
手順3(1)または2(3)
【問題2】
12345→12534
手順5(2)
【問題3】
12345→13542
手順2(2),5(2)
【問題4】
12345→14253
手順4(2),5(3)
【問題5】
12345→13524
手順2(2),1(3)
【問題6】
12345→15432
手順5(3),2(3),4(2)
【おまけ】
操作X1(一つ離れている文字と交換)と12345→15423のような操作
(1と4の交換、つまり二つ離れている文字と交換)(操作=X(2)W(3))
ができるため他の操作この二つの操作の組合せによってつくれます。
| パターン数= | 5! 5 |
=24 |
24パターンのなか、動かす前のパターン(12345)をひいたら、23パターンになります。
問題1)から3)のような操作とX(2)W(3)の操作がそれぞれ違った5パターンに並べられます。
(手順数=1、1、2、2)
あと3つは問題4)から6)のようなパターンです。
(手順数=2、2、3)
◆広島県 清川 育男 さんからの解答
【問題1】 屋1
【問題2】 部2
【問題3】
の1→部1
部1→の1
【問題4】
数2→の1
学2→部1
の2→屋1
部2→数1
屋2→学1
【問題5】
数1→屋2
学1→数2
の1→学2
部1→の2
屋1→部2
【問題6】
数 1 屋 1 学 2
数 1 学 1 の 2
数 1 学 2 屋 1
数 1 の 2 学 1
数 2 屋 1 部 1
数 2 部 1 屋 1
学 1 数 1 の 2
学 1 の 1 部 2
学 1 の 2 数 1
学 1 部 2 の 1
学 2 数 1 屋 1
学 2 屋 1 数 1
の 1 部 1 屋 2
の 1 部 2 学 1
の 1 屋 2 部 1
の 1 学 1 部 2
の 2 数 1 学 1
の 2 学 1 数 1
部 1 数 2 屋 1
部 1 の 1 屋 2
部 1 屋 1 数 2
部 1 屋 2 の 1
部 2 の 1 学 1
部 2 学 1 の 1
屋 1 数 1 学 2
屋 1 数 2 部 1
屋 1 学 2 数 1
屋 1 部 1 数 2
屋 2 部 1 の 1
屋 2 の 1 部 1
【おまけ】
F(部3)=F(数1)
F(屋3)=F(学1)
F(数3)=F(の1)
F(学3)=F(部1)
F(の3)=F(屋1)
以上の関係から「3」は不必要。
F(X2)+F(X2)
F(数1)+F(部1)
F(学1)+F(屋1)
F(の1)+F(数1)
F(部1)+F(学1)
F(屋1)+F(の1)
以上の操作は元に戻ってしまう。
F(X1)+F(X1)=F(X2)
F(X1)+F(X2)=F(X3)=F(Y1)
F(X2)+F(X1)=F(X3)=F(Y1)
F(X1)+F(X1)+F(X1)=F(X3)=F(Y1)
X<>Y
以上の関係が成り立つ。
●元に戻すための最小の置換回数と手数との関係 数学の部屋
置換回数
A)
数学屋部の (3)
屋 1
数部の学屋 (3)
部 1
数部屋の学 (5)
の 1
数屋の部学 (5)
学 1
数屋部学の (5)
数 1
B)
数の学屋部 (2)
数 2
数の屋部学 (4)
の 2
数部の屋学 (4)
屋 2
数屋学部の (4)
学 2
数屋の学部 (4)
部 2
C)
数学部屋の (2)
数 1 学 1
学 1 数 1
数学屋の部 (2)
の 1 部 1
部 1 の 1
数の部学屋 (2)
数 1 屋 1
屋 1 数 1
数部学の屋 (2)
学 1 の 1
の 1 学 1
数部屋学の (4)
部 1 屋 1
屋 1 部 1
D)
数学の屋部 (1)
学 1 部 2
部 1 屋 2
部 2 学 1
屋 2 部 1
数学部の屋 (1)
数 1 の 2
の 1 部 2
の 2 数 1
部 2 の 1
数の学部屋 (1)
学 1 の 2
学 2 屋 1
の 2 学 1
屋 1 学 2
数の部屋学 (3)
数 1 学 2
数 2 部 1
学 2 数 1
部 1 数 2
数屋学の部 (3)
数 2 屋 1
の 1 屋 2
屋 1 数 2
屋 2 の 1
E)
数の屋学部 (3)
数 1 屋 2
学 1 数 2
の 1 学 2
部 1 の 2
屋 1 部 2
数部学屋の (3)
数 2 の 1
学 2 部 1
の 2 屋 1
部 2 数 1
屋 2 学 1
F)
数屋部の学 (6)
数 1 屋 1 学 2
数 1 学 1 の 2
数 1 学 2 屋 1
数 1 の 2 学 1
数 2 屋 1 部 1
数 2 部 1 屋 1
学 1 数 1 の 2
学 1 の 1 部 2
学 1 の 2 数 1
学 1 部 2 の 1
学 2 数 1 屋 1
学 2 屋 1 数 1
の 1 部 1 屋 2
の 1 部 2 学 1
の 1 屋 2 部 1
の 1 学 1 部 2
の 2 数 1 学 1
の 2 学 1 数 1
部 1 数 2 屋 1
部 1 の 1 屋 2
部 1 屋 1 数 2
部 1 屋 2 の 1
部 2 の 1 学 1
部 2 学 1 の 1
屋 1 数 1 学 2
屋 1 数 2 部 1
屋 1 学 2 数 1
屋 1 部 1 数 2
屋 2 部 1 の 1
屋 2 の 1 部 1
●アプローチの方針
F(部3)=F(数1)
F(屋3)=F(学1)
F(数3)=F(の1)
F(学3)=F(部1)
F(の3)=F(屋1)
以上の関係から「3」は不必要。
1)F(数1)*F(部1)
2)F(学1)*F(屋1)
3)F(の1)*F(数1)
4)F(部1)*F(学1)
5)F(屋1)*F(の1)
6)F(数2)*F(数2)
7)F(学2)*F(学2)
8)F(の2)*F(の2)
9)F(部2)*F(部2)
10)F(屋2)*F(屋2)
以上の操作は元に戻る。
11)F(数1)*F(数1)=F(数2)
12)F(学1)*F(学1)=F(学2)
13)F(の1)*F(の1)=F(の2)
14)F(部1)*F(部1)=F(部2)
15)F(屋1)*F(屋1)=F(屋2)
16)F(数1)*F(数2)=F(の1)
17)F(数2)*F(数1)=F(の1)
18)F(学1)*F(学2)=F(部1)
19)F(学2)*F(学1)=F(部1)
20)F(の1)*F(の2)=F(屋1)
21)F(の2)*F(の1)=F(屋1)
22)F(部1)*F(部2)=F(数1)
23)F(部1)*F(部2)=F(数1)
24)F(屋1)*F(屋2)=F(学1)
25)F(屋2)*F(屋1)=F(学1)
以上の関係が成り立つ。
F( )を5行5列の正方行列で表す。
元に戻る操作は単位行列とする。
5行5列の正方行列は25個の要素で構成されるので、上記25個の関係式から一意に決まるはずである。
F( )の操作を以下のように定義する。
(1,5)*(5,5)=(1,5) 数 1
学 2
の 3
部 4
屋 5
数学の部屋=(1,2.3,4,5)
今回の問題は行列の積の問題に還元される。
実際のモデルが提示出来ればいいのですが、、、。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 屋1
【問題2】 部2
【問題3】 部1→の1
【問題4】 数2→の1
【問題5】 屋1→部2
【問題6】 屋1→数2→部1
【おまけ】
3回以内で可能である。
全部で5×3=15種の操作があるが、このうち同じ結果になるものを除くと表1に示すように10種である。
これらは「学」〜「屋」の4個の置換であり、この中に互換が3種含まれている。
(表1tagオレンジ)
残り3種の互換は表2に示すように2操作で合成可能である。
全ての4要素置換は最大3種の互換で合成可能であるから、任意の並びにすることが可能である。
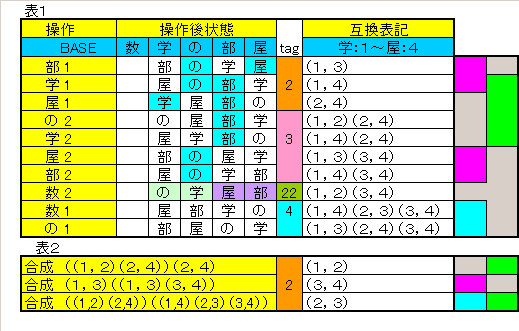
表3は無&1操作後状態の11種の状態を並べた直した表である。
表3に示すように、1回以下の操作で任意の並びと多くても1互換差状態にすることが可能である。
一方、互換は最大2操作で実現できる。
よって最大3操作で可能である。
◆ 問題へもどる
◆ 今週の問題へ