◆愛知県 Y.M.Ojisan さんからの解答
105回の解答の続きとして記述。
ただし、全て5を法とする。
計算すると rank(A)=8 である。
従って、Aの8×8の小行列の逆行列を用いて、下記逆行列もどきBを作成する。
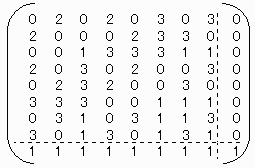
D=0 のとき、B×C=−B×A×N であって、
−B×Aは
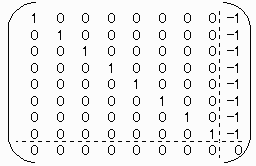
従って,解が存在するためには ΣCi=0 でなければならず、この時5つの解が存在して
N=B×C+t*[1,1,1,1,1,1,1,1,1]' t=0,1,2,3,4 である。 ―――(1)
【問題1】
1、3,4,5,6,8
問題の作り方が既知なので
解の一つは[0,4,0,0,0,0,4,0,4] である。
従って、その他の解は(1)より
[1,0,1,1,1,1,0,1,0] ,
[2,1,2,2,2,2,1,2,1],
[ 3,2,3,3,3,3,2,3,2],
[4,3,4,4,4,4,3,4,3] 。(転置省略)
クリック数が最少は 他の解の1番目であって、
1、3,4,5,6,8 である。
【問題2】
1、3,7,9
C=[2,3,2,3,0,3,2,3,2] である。
(1)より t=0の解は N'=[0,4,0,4,4,4,0,4,0]。
さらに、
t=1:[1,0,1,0,0,0,1,0,1] ,
t=2:[2,1,2,1,1,1,2,1,2] ,,,,,, 。
クリック数が最少は t=1の場合であって、
1、3,7,9 である。
◆広島県 清川 育男 さんからの解答
時間切れになりましたが解答プログラムを作ってみました。
意見がわかれているように思うのですが(問題の捕らえかたの違い)、3色のときは任意の図柄を作ることが可能ですが、他の場合は任意の図柄を作ることが出来ません。
作ることの出来る図柄は当然のこと初期状態に戻せます。
REM 解答プログラム
SET ECHO "OFF"
DIM A(9)
DIM B(9)
DIM C(9)
PRINT "色数 ";
INPUT K
PRINT K
PRINT "色番号"
FOR I=1 TO 9
PRINT I;" ";
INPUT A(I)
PRINT A(I)
NEXT I
PRINT
LET SONZAI=0
FOR I1=0 TO K-1
LET B(1)=I1
FOR I2=0 TO K-1
LET B(2)=I2
FOR I3=0 TO K-1
LET B(3)=I3
FOR I4=0 TO K-1
LET B(4)=I4
FOR I5=0 TO K-1
LET B(5)=I5
FOR I6=0 TO K-1
LET B(6)=I6
FOR I7=0 TO K-1
LET B(7)=I7
FOR I8=0 TO K-1
LET B(8)=I8
FOR I9=0 TO K-1
LET B(9)=I9
LET C(1)=I1+I2+I3+I4+I7
LET C(2)=I1+I2+I3+I5+I8
LET C(3)=I1+I2+I3+I6+I9
LET C(4)=I1+I4+I5+I6+I7
LET C(5)=I2+I4+I5+I6+I8
LET C(6)=I3+I4+I5+I6+I9
LET C(7)=I1+I4+I7+I8+I9
LET C(8)=I2+I5+I7+I8+I9
LET C(9)=I3+I6+I7+I8+I9
FOR I=1 TO 9
LET C(I)=REMAINDER(C(I),K)
NEXT I
LET F=0
FOR I=1 TO 9
IF C(I)<>A(I) THEN
LET F=1
EXIT FOR
END IF
NEXT I
IF F=0 THEN
LET SONZAI=1
PRINT "図柄を作る手順"
FOR I=1 TO 9
PRINT B(I);
NEXT I
PRINT
PRINT
FOR I=1 TO 9
PRINT C(I);
IF MOD( I , 3) =0 THEN
PRINT
END IF
NEXT I
PRINT
LET Z=0
FOR I=1 TO 9
IF B(I)<>0 THEN
LET Z=Z+K-B(I)
END IF
NEXT I
PRINT "初期状態に戻す手順"
FOR I=1 TO 9
IF B(I)<>0 THEN
PRINT K-B(I);
ELSE
PRINT B(I);
END IF
NEXT I
PRINT " ";Z;"回"
PRINT
END IF
NEXT I9
NEXT I8
NEXT I7
NEXT I6
NEXT I5
NEXT I4
NEXT I3
NEXT I2
NEXT I1
IF SONZAI=0 THEN
PRINT "図柄を作ることが出来ない。"
END IF
END◆海外 ふぬーる さんからの解答
【おまけ2】
一回のクリックによる色番号の変化は例として次のようになる。
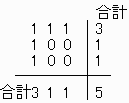
各マスは
5−c(i)回色番号が増加すれば赤になる。
ただし、現在赤いマスは0回でよいので、5で法を取り、
(5-c(i))mod 5となる。
全てのマスの色番号の和を取ると、一回のクリックで色番号の和は5増加する。
従って、初期状態に戻すのに必要なクリック回数Nは、
N=Σn(i)=Σ{(5-c(i))mod 5}/5
次に、各行列毎の色番号の和について考えてみる。
一回のクリックで、クリックしたマスを含む行及び列は色番号の和は3増加する。
その他の行・列では1増加する。
初期状態に戻るのに必要な色番号の増加分の和Δは、1行目を例にとると、
Δ=(5-c(1))mod 5+(5-c(2))mod 5+(5-c(3))mod 5このうち、1行目でクリックする回数をl(1)とすると、
Δ
=3l(1)+(N−l(1))
=2l(1)+N
l(1) =(Δ−N)/2 =[(5-c(1))mod 5+(5-c(2))mod 5+(5-c(3))mod 5−Σ{(5-c(i))mod 5}/5] /2同様にして、
l(2)=[(5-c(4))mod 5+(5-c(5))mod 5+(5-c(6))mod 5−Σ{(5-c(i))mod 5}/5] /2 l(3)=[(5-c(7))mod 5+(5-c(8))mod 5+(5-c(9))mod 5−Σ{(5-c(i))mod 5}/5] /2また、各列のクリック回数をmとして、
m(1)=[(5-c(1))mod 5+(5-c(4))mod 5+(5-c(7))mod 5−Σ{(5-c(i))mod 5}/5] /2 m(2)=[(5-c(2))mod 5+(5-c(5))mod 5+(5-c(8))mod 5−Σ{(5-c(i))mod 5}/5] /2 m(3)=[(5-c(3))mod 5+(5-c(6))mod 5+(5-c(9))mod 5−Σ{(5-c(i))mod 5}/5] /2次に各マスのクリック回数を求める。
1番のマスについて考えると、1行目でのクリック回数と1列目でのクリック回数の和は、1行1列すなわち1番目のマスでのクリック回数を二重にカウントしている。
よって、
n(1)=l(1)+m(1)-(5-c(1))mod 5
3j+k番目(j=0,1,2 k=1,2,3)のマスについて、
n(3j+k) =l(j+1)+m(k)-(5-c(3j+k))mod 5 = [(5-c(3j+1))mod 5+(5-c(3j+2))mod 5+(5-c(3j+3))mod 5−Σ{(5-c(i))mod 5}/5] /2+[(5-c(k))mod 5+(5-c(3+k))mod 5+(5-c(6+k))mod 5−Σ{(5-c(i))mod 5}/5] /2 −(5-c(3j+k))mod 5【問題1】

クリック回数
2+2-3=1 2+2-4=0 2+2-3=1
3+2-4=1 3+2-4=1 3+2-4=1
1+2-3=0 1+2-2=1 1+2-3=0
答え 1,3,4,5,6,8(順不同)
【問題2】
答え 1,3,7,9
◆山梨県 Footmark さんからの解答
マス番号の付け方は次の8通りのいずれかとし
789 123 987 321 456 456 654 654 123 789 321 987 369 963 147 741 258 852 258 852 147 741 369 963マス番号をiとした時の
そのマス自身 ・・・ 自(i) 同行∨同列4マス ・・・ 同(i) 別行∧別列4マス ・・・ 別(i) そのマス自身の色番号 ・・・ N(i) 同行∨同列4マスの色番号の合計 ・・・ N同(i) 別行∧別列4マスの色番号の合計 ・・・ N別(i)で表すものとする。
色数がnの時、いかなる状態からでも同一のマスをn回クリックすると元の状態に戻ってしまうから、何もしなかったのと同じことになる。
それ故、どんな実クリック数も、たかだか
0≦有効クリック数≦n−1
の範囲の有効クリック数に置き換えられる。
式で表すと次のようになる。
有効クリック数=MOD(実クリック数/n)
ただし、MOD[P/Q]はPをQで割った時の余りR
(Rは0≦R<Qの整数)を表す。
今後はクリック数とは有効クリック数のことを言う。
また、初期状態からの各マスのクリック数さえ分かれば、初期状態に戻すための各マスのクリック数もおのずと導き出せる。
すべてのマスを初期状態から何もしなかったことにすれば良いからである。
色数がnの時、各々のマスごとに初期状態からの総クリック数が0かnになるように、
その後のクリック操作{0〜(n−1)}をすれば良い。
このことは、初期状態からのクリック操作によって作成されたすべての状態は,色数nやクリック順に関係なく各マスごとに適切な回数だけのクリック操作をさらに与えることで例外なく初期状態に戻すことが可能なことを意味する。
色数n、マス番号iとし、
初期状態からのそのマスのクリック数をS(i)とすれば、
初期状態に戻すためのそのマスのクリック数C(i)は
C(i)=MOD[{n−S(i)}/n]
で表される。
ところが、初期状態からの各マスのクリック数S(i)は分かっていない。
分かっているのは、変化させられた各マスの色番号N(i)である。
しかし、与えられた各マスの色番号N(i)より初期状態からの各マスのクリック数S(i)が導き出せれば上式により初期状態に戻すための各マスのクリック数C(i)もおのずと導き出せることになる。
【2色の時の考察】
2色の時は、与えられた個々の状態の正解を出すのはさほど困難ではない。
しかし、一般的な解となると一番厄介である。
と言うのは、異なったクリック操作で同一の効果が生じたり、初期状態に戻すための解答も幾通りもあったりするからである。
2色の時に限り、色番号が1つ進むと0が1に1が0に変化するので、これを「反転する」と表現させてもらう。
反転とはマスの色番号と1とで排他的論理和(Xor)させるのと同じである。
2色の時、同じマスを2回クリックするとすべて元に戻ってしまい何もしないのと同じなので、以下クリックとはすべて1回のことを指す。
9個のマスのどのマスをクリックしたかが分かればそのマスをもう1回ずつクリックすれば初期状態に戻すことが可能である。
マス番号iの1回のクリック操作により自(i)の1マスと同(i)の4マスの色番号が反転されるが、
N同(i)の変化は、同行2マス同列2マスの4マスが同時に反転するため、
−4,−2,±0,+2,+4のいずれかである。
また、同(i)、別(i)のそれぞれの任意の1マスのマス番号をp,qとすると
N同(p)の変化も,同行か同列のどちらかの2マスが同時に反転するため、
−2,±0,+2のいずれかである。
N同(q)の変化も,同行1マス同列1マスの2マスが同時に反転するため、
−2,±0,+2のいずれかである。
しかも、任意のマスの色番号N(i)において常に
0≦N(i)≦1
を満たさなければならない。
また、問題の定義より、初期状態ではすべてのマスの色番号が0である。
これらのことより、初期状態から作成されたいかなる状態も、
任意のマス番号iにおいてN同(i)は常に0か2の倍数である。
すなわち、2色の時に限り任意のマスからみて同行同列4マスの色番号の和は常に0か偶数である。
これを満たさない状態は決して初期状態から生じないしその状態を初期状態に戻すのも明らかに不可能である。(必要条件)
マス番号iの1回のクリック操作により色番号が反転するのは
自(i)1マスと同(i)4マスであるから、色番号が1のマスは
自(i)による変化か同(i)による変化かまたはその両方かのいずれかである。
ところが、常にN同(i)は0か2の倍数であるから同(i)4マスの内の色番号が1のマスは0個か偶数個あり、そのマスをクリックしても2色の時に限りN(i)になんら影響を与えない。
それ故、任意のマス番号iにおいて常にN同(i)が0か2の倍数である限り、
自(i)による変化か同(i)による変化かの区別なく色番号が1のマスすべてをクリックしても、
自(i)による変化の場合だけが有効になるため、初期状態に戻る。
(ただし初期状態に戻すための解であって最小クリック数の保証はない)
このことより、2色の時に限りいかなるマスからみても同行同列4マスの色番号の和が0か偶数であるような状態は例外なく初期状態に戻せるし、このような状態はすべて初期状態から作成することが可能である。(十分条件)
任意の同行3マス(3通り)か、あるいは任意の同列3マス(3通り)をクリックすると、すべてのマスの色番号が反転する。
もう1度、上の6通りの方法の内の1方法を実行すると、すべてのマスが反転状態からさらに反転して元に戻ってしまい、何もしないことになる。
この組み合わせの数は(6X6=)36通りあるが、これから1回目と2回目が同じ操作の場合は同行3マスか同列3マスを2回ずつクリックしたことになるため、
この6通りを除くと(36−6=)30通りになる。
また、1回目と2回目の順序は問題ではないので(30/2!=)15通りになる。
この15通りのクリック操作のマスのグループは次の通りである。
(行と列の交点に当たるマスは2回クリックされるのでクリックは無いものとなる)
(平行型)
111 111 000 111 000 111 000 111 111 011 101 110 011 101 110 011 101 110(同行同列型)
011 101 110 100 010 001 100 010 001 100 010 001 011 101 110 100 010 001 100 010 001 100 010 001 011 101 110平行型が6グループで同行同列型が9グループの15グループだが
平行型の6グループでは6個のマスに1があるが、この1のあるマスをすべてクリックすれば何もしないことになる。
同行同列型の9グループでは4個のマスに1があるが、この1のあるマスをすべてクリックすれば何もしないことになる。
このようなマス群をお互いに「補の関係にある」と呼び、
9個のマスを0/1で埋めた上のようなおのおののグループを「補表」と呼ぶことにする。
仮に補の関係にあるマスの内の幾つかをクリックしたとしよう。
すると、その状態から元の状態に戻すには2通り考えられる。
1つは、今クリックしたマスをもう1度クリックしてやれば、各々のマスを結局2回クリックしたことになるため元に戻る。
もう1つの方法は、補の関係にある残りのマスをすべてクリックすれば、結局補の関係にあるマスをすべてクリックしたことになるため元に戻る。
このことから、1番目の方法のクリック操作と2番目の方法のクリック操作とは与える効果が等しいため同等であると言える。
仮に同行同列型のように4つのマスが補の関係にある場合、その内の3マスのクリック操作は残りの1マスのクリック操作に置き換えることが出来る。
一般的に使用する色数nにおいて補表が存在すれば置き換え操作も必ず存在し、その置き換え操作とは9個のマスのクリック数と任意の補表とで対応したマスごとに次式で与える変換をさせることである。
新クリック数=MOD{(旧クリック数+補表のクリック数)/n}
ところが、2色の場合に限りこの変換は、
9個のマスのクリックの有(1)/無(0)と任意の補表とで対応したマスごとに排他的論理和(Xor)をさせることになる。
この置き換え操作をいろいろな補表と何回も行っても、与える効果はすべて等しいため同等である。
補の関係を利用すると4マス以上のクリックは、すべて3マス以内のクリック)に置き換えられるため、2色の時のあらゆる状態はたかだか3マス以内のクリックで作成されるし、その解もまた3マス以内のクリックで済む。
仮に初期状態に戻すための解が1つ分かったとしよう。
すると、任意の回数その解の置き換え操作したものも、やはり1つの解である。
2色の時、マスの色番号をそのマスのクリック数とするのも1つの解であるから、その解に合計クリック数が3回以内になるまで置き換え操作をさせて得た結果が最小クリック数の解である。
【2色の時の解答】
マス群とは選択した1個以上のマスを指す。
2色の時は全く異なったマス群のクリック操作でも同一の結果を与える。
それ故、あるマス群のクリック操作は別のマス群のクリック操作に置き換えられる。
4マス以上のクリック操作も、すべて3マス以下のクリック操作に置き換えられる。
それ故、結果として与える場合の数はマス群の組み合わせの場合の数に比べて著しく少なく、生じ得る状態は以下の通りである。
無操作 初期状態 ・・・ 1通り 計 1通り 1マスのクリック操作 色番号1が5マス ・・・ 9通り 計 9通り 2マスのクリック操作 色番号1が4マス ・・・ 9通り 6マス ・・・ 6通り 計15通り 3マスのクリック操作 色番号1が3マス ・・・ 6通り 色番号1が9マス ・・・ 1通り 計 7通り生じ得る状態は32パターンあるが、回転させれば重なるような状態は1つとすると下記の12パターンしかあり得ない。
<0> <3> <4> 000 001 010 011 101 101 000 010 001 011 101 000 000 100 100 000 000 101 (X1) (X2)(X4) (X4)(X4)(X1) <9> <6> <5> 111 110 101 100 010 010 111 101 110 100 010 111 111 011 011 111 111 010 (X1) (X2)(X4) (X4)(X4)(X1)これらの12パターンの状態を、初期状態に戻すためににクリックすべきマスは次の通りである。
出題時の色番号に1が0個なら、既に初期状態。
出題時の色番号に1が3個なら、その3マス。
出題時の色番号に1が4個なら、交点以外の0の同行2マスか同列2マス。
出題時の色番号に1が5個なら、1の交点1マス。
出題時の色番号に1が6個なら、1が2個ある方の対角線上のその2マス。
出題時の色番号に1が9個なら、任意の1行か任意の1列の3マス。
【3色の時の考察】
3色の時は、与えられた個々の状態の正解を出すのは多少困難である。
しかし、一般的な解となるといたって簡単である。
3色の時はマス番号iにおいて、
N同(i)やN別(i)は不変のままN(i)だけ1つだけ更新させるのが可能で
自(i)1マスと別(i)4マスの計5マスを1回ずつクリックすれば良い。
このことを利用すると、マス番号iのマスの色番号を0に戻すには
回数(i)=MOD[{3−N(i)}/3]
で与えられる回数(i)だけ各々のマスごとに、自(i)1マスと別(i)4マスをクリックすれば良いことになる。
(初期状態に戻すため1方法である)
しかし、各マスごとにこの操作を行うと,どこかのマスでクリック数が3回以上になってしまうこともあり得るので最小クリック数の解である保証はない。
マス番号iにおいて自(i)のクリックの要請は、N(i)1マスの更新のための要請と別(i)の4マスの色番号の更新のための要請があり、
それらすべての要請分だけクリックしなければならないから、
別(i)の4マスをそれぞれ別(i)1,別(i)2,別(i)3,別(i)4とすると、
各々のマスの色番号を0に戻すためのクリック数C(i)は
C(i)
=MOD[{(3−N(i))+(3−別(i)1の色番号)+(3−別(i)2の色番号)+(3−別(i)3の色番号)+(3−別(i)4の色番号)}/3]
=MOD[{15−(N(i)+N別(i))}/3]
ところが、各々のマスの最大色番号は2なので、
それ故、上式の 15−(N(i)+N別(i)) は、mを整数とすると
3m−(N(i)+N別(i))≧0 を保証する最小値で十分なので
C(i)=MOD[{12−(N(i)+N別(i))}/3]
3色の時、2色の時のような補の関係にあるマスのグループはなく、
上式のC(i)は明らかに3回以上にならないため、最小クリック数の解である。
すなわち、出題時の色番号表から、それぞれのマスごとに上式で必要クリック数を求めればそれが最小クリック数の解である。
【3色の時の解答】
マス番号(1〜9)における出題時の各マスのの色番号を(N(1)〜N(9))とすれば、
求める各マスのクリック数(C(1)〜C(9))は次式で表される。
C(1)=MOD[{12−(N(1)+N(5)+N(6)+N(8)+N(9))}/3]
C(2)=MOD[{12−(N(2)+N(4)+N(6)+N(7)+N(9))}/3]
C(3)=MOD[{12−(N(3)+N(4)+N(5)+N(7)+N(8))}/3]
C(4)=MOD[{12−(N(4)+N(2)+N(3)+N(8)+N(9))}/3]
C(5)=MOD[{12−(N(5)+N(1)+N(3)+N(7)+N(9))}/3]
C(6)=MOD[{12−(N(6)+N(1)+N(2)+N(7)+N(8))}/3]
C(7)=MOD[{12−(N(7)+N(2)+N(3)+N(5)+N(6))}/3]
C(8)=MOD[{12−(N(8)+N(1)+N(3)+N(4)+N(6))}/3]
C(9)=MOD[{12−(N(9)+N(1)+N(2)+N(4)+N(5))}/3]
【5色の時の考察】
5色の時は、与えられた個々の状態の正解を出すのは非常に困難である。
しかも、3色の時のようにN同(i)やN別(i)は不変のままN(i)だけ更新させるのは不可能なので色数の多い分、一般的な解もなかなか一筋縄ではいかない。
マス番号iの1回のクリック操作により自(i)の1マスと同(i)の4マスの色番号が1つ更新されるが、それぞれのマスを考えると
(0→1),(1→2),(2→3),(3→4)のように色番号が1増えるか、
(4→0)のように色番号が4減るかのどちらかである。
この時の5マスの色番号の変化量の組み合わせは以下の場合しかあり得ない。
5X(+1) + 0X(−4) = + 5 4X(+1) + 1X(−4) = ± 0 3X(+1) + 2X(−4) = − 5 2X(+1) + 3X(−4) = −10 1X(+1) + 4X(−4) = −15 0X(+1) + 5X(−4) = −20また、いかなる全9マスの色番号の状態も、上に示した限りの色番号の変化の繰り返しでしかない。
0≦N(i)≦4
を満たさなければならない。
また、問題の定義より、初期状態ではすべてのマスの色番号が0である。
これらのことより、初期状態から作成されたいかなる状態も、全9マスの色番号の合計は常に0か5の倍数である。
これを満たさない状態は決して初期状態から生じないしその状態を初期状態に戻すのも明らかに不可能である。
5色の時は、全9マスを1回ずつクリックすると元の状態に戻ってしまい、何もしなかったのと同じことになる。
当然、この操作をm回(1≦m≦4)繰り返しても何もしなかったのと同じ筈である。
それ故、5色の時の補表は以下の4つである。
111 222 333 444 111 222 333 444 111 222 333 444また、クリック数の置き換え操作とは全9マスのクリック数と任意の補表とで対応したマスごとに次式で与える変換をさせることである。
新クリック数=MOD{(旧クリック数+補表のクリック数)/5}5色の時のこの補表は全9マスに及ぶため、各マスのそれぞれの初期状態からの総クリック数が全9マスとも補表のクリック数になるようにすれば、全9マスとも何もしなかったことになり初期状態に戻る特徴がある。000 111 222 333 444 000 111 222 333 444 000 111 222 333 444各マスの初期状態からのクリック数は5種類(0〜4)あるが、明らかにその5種類が均等の数ある時が最小クリック数は最大になる筈である。
初期状態からのクリック数が0のマス 2マス 初期状態からのクリック数が1のマス 2マス 初期状態からのクリック数が2のマス 2マス 初期状態からのクリック数が3のマス 2マス 初期状態からのクリック数が4のマス 1マスとすると
9マスとも初期状態からの総クリック数を0にするには、19クリック 9マスとも初期状態からの総クリック数を1にするには、18クリック 9マスとも初期状態からの総クリック数を2にするには、17クリック 9マスとも初期状態からの総クリック数を3にするには、16クリック 9マスとも初期状態からの総クリック数を4にするには、20クリックよって、5色の時のあらゆる状態は16回以内のクリックで作成されるし、その解もまた16回以内のクリックで済む。
マス番号をiとした時の
そのマス自身の初期状態からのクリック数 ・・ S(i) 同行∨同列4マスの初期状態からのクリック数の合計 ・・ S同(i) 別行∧別列4マスの初期状態からのクリック数の合計 ・・ S別(i)で表すものとする。
色数は無限色あるものとし、
そのマス自身の色番号 ・・・ n(i) 同行∨同列4マスの色番号の合計 ・・・ n同(i) 別行∧別列4マスの色番号の合計 ・・・ n別(i)で表すものとすると、
n(i) = S(i) + S同(i) n同(i) = 4S(i) + 2S同(i) + 2S別(i) n別(i) = 2S同(i) + 3S別(i)で与えられるが、
n同(i)
= 4S(i) + 2S同(i) + 2S別(i)
= 2S(i) + 2*{S(i) + S同(i) + S別(i)}
しかし、2*{S(i) + S同(i) + S別(i)} は、全9マスのクリックを2度したことになるため無視できる。
S(i) = n同(i)/2
ここで、色数を無限色から5色にし、n同(i)をN同(i)に置き直すと
n同(i) = N同(i) + 5m
(ただしmは整数で 0≦m≦4)
S(i) = MOD[{(N同(i) + 5m)/2}/5]
(ただしmは整数で 0≦m≦4)
この式でmが0,2,4のいずれの場合も5mの項は結果的には0となり、
mが1,3のいずれの場合も5mの項は結果的には等しくなる。
それ故、上式は
S(i) = MOD[{(N同(i) + 5m)/2}/5]
(ただしmは整数で 0≦m≦1)
に、置き換えられる。
(N同(i) + 5m)/2 が常に整数であるためには、
(N同(i) + 5m) は常に0か2の倍数でなければならないから、
N同(i)が0か偶数の時は m=0 にして、
N同(i)が奇数の時は m=1 にすれば良いことになる。
それ故上式は
S(i) = MOD[{(N同(i) + 5*MOD(N同(i)/2))/2}/5]
になる。マス番号iにおける初期状態に戻すためのクリック数C(i)は
C(i) = MOD[{5−S(i)}/5]
であるが、同(i)4マスのいかなる色番号の組み合わせの場合を考えても
0 ≦ (N同(i) + 5*MOD(N同(i)/2))/2 ≦ 10であるから
C(i)=MOD[[10-{(N同(i)+5*MOD(N同(i)/2))/2}]/5]
となる。
これは全9マスの色番号を初期状態に戻すための、任意のマス番号iにおける1つの解である。
(ただし、最小クリック数の解である保証はない)
【5色の時の解答】
任意のマス番号iにおいて、ある1つの解でのクリック数を c(i) で表す時、
◆ 問題へもどる
◆ 今週の問題へ
最小クリック数の解でのクリック数を T
マス番号(1〜9)における出題時の各マスの色番号を(N1〜N9)とすれば、
求める各マスのクリック数(C1〜C9)は次式で表される。C1=T<MOD[[10-{(N2+N3+N4+N7+5*MOD((N2+N3+N4+N7)/2))/2}]/5]>
C2=T<MOD[[10-{(N1+N3+N5+N8+5*MOD((N1+N3+N5+N8)/2))/2}]/5]>
C3=T<MOD[[10-{(N6+N9+N2+N1+5*MOD((N6+N9+N2+N1)/2))/2}]/5]>
C4=T<MOD[[10-{(N7+N1+N5+N6+5*MOD((N7+N1+N5+N6)/2))/2}]/5]>
C5=T<MOD[[10-{(N2+N8+N4+N6+5*MOD((N2+N8+N4+N6)/2))/2}]/5]>
C6=T<MOD[[10-{(N3+N9+N5+N4+5*MOD((N3+N9+N5+N4)/2))/2}]/5]>
C7=T<MOD[[10-{(N4+N1+N8+N9+5*MOD((N4+N1+N8+N9)/2))/2}]/5]>
C8=T<MOD[[10-{(N9+N7+N5+N2+5*MOD((N9+N7+N5+N2)/2))/2}]/5]>
C9=T<MOD[[10-{(N8+N7+N6+N3+5*MOD((N8+N7+N6+N3)/2))/2}]/5]>
ただし、最小クリック数の解とは、ある1つの解とある1つの解を下記の4個の補表で置き換え操作させた4つの解の合わせて5つの解の内で、全9マスのクリック数の合計が最小となる解のことである。111 222 333 444
111 222 333 444
111 222 333 444
また、置き換え操作とは全9マスのクリック数と上記の補表とで対応したマスごとに次式で与える変換をさせることである。新クリック数=MOD{(旧クリック数+補表のクリック数)/5}