『今週の問題』第105回　解答

◆愛知県　Y.M.Ojisan さんからの解答

【一般に】

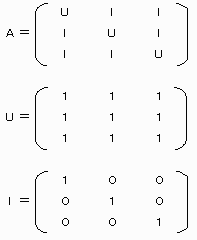
Ｃ＝[c1,c2,c3,c4,c5,c6,c7,c8,c9]t　　の状態に対し
Ｎ＝[n1,n2,n3,n4,n5,n6,n7,n8,n9]t　　なる手をうち
Ｄ＝[d1,d2,d3,d4,d5,d6,d7,d8,d9]t　　になったとするとき、これらは下記線形方程式を満たす。

ここで P は色の数であり、１０５回の場合３である。

Ｄ＝Ｃ＋Ａ×Ｎ　mod P

行列Ａの逆行列の存否はdet(Ａ)が０かどうかで決まるが、これを計算すると、

　det(Ａ)　mod P ＝　８０ mod P　である。

従って、Pが２（１０４回の場合）または５の倍数でなければ、Ａの逆行列が存在する。

この場合解は唯一であって、Ｄ＝０（全部赤）の解は　

Ｎ＝−Ａ-1×Ｃ　mod P　　―――――（１）　である。

なお　−Ａ-1　は計算すると下記である。

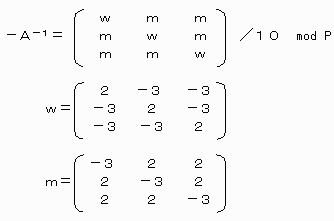
特にP=3 の時　−３→０　、２／１０→２ である。

【問題１】

P=3とし、
Ｃ＝[0,2,0,2,0,2,0,2,0]t　を式（１）に代入し計算すると
Ｎ＝[2,0,2,0,0,0,2,0,2]t である。すなわち

1，1，3，3，7，7，9，9

【問題２】

P=3とし、
Ｃ＝[2,2,2,2,2,2,2,1,2]t　を式（１）に代入し計算すると
Ｎ＝[0,2,0,0,2,0,2,0,2]t である。すなわち

2，2，5，5，7, 7，9，9

【おまけ１】

本問題は【一般に】のP=3の場合である。
従って、逆行列が存在し、解は必ず、かつPを法として唯一存在する。

【おまけ２】

【おまけ１】に示したように「３を法として解は唯一」であり、これが最小手数である。

【Ｐ．Ｓ．】

１０４回の場合は　det(A)=0 であり、
計算すると、rank(A)=5 なので解が複数存在(29-5=16個／ただし３手以上を含む)したり、存在しなかったりすることも(1)より分かる。
なお、「４色」もそうだが、「５色」が次におもしろそうだ。

◆岡山県の中学校３年生　葵 さんからの解答

【問題１】

1，3，7，9，1，3，7，9

【問題２】

2，7，9，5，2，7，9，5

問題を作る時点でクリックされた回数×２が、必要な回数

例外→問題を作る時点で、繰り返してクリックされている場合
　[1,2,1､]

この場合、『1,2,1,1,2,1､』でとくことも可能。
しかし、基本を、1,2。最後の1を1,2の繰り返しの始まりの1だと考えれば、
『2,1,2』の3回でとくことができる。

つまり、3回（同じ押し方を）繰り返せば、初期設定に戻すことは可能。

従って、
問題1は、「1,3,7,9､」によって作成されているので、
それ（1,3,7,9､）×2

問題2は、｢2,7,9,5｣によって作成されているので、
それ（2,7,9,5､)×2が､手順になる。

◆広島県　清川　育男 さんからの解答

【問題１】

1，3，7，9，1，3，7，9 （順不同）

【問題２】

2，5，7，9，2，5，7，9 （順不同）

【おまけ１】

An(n=1-9)
An mod 3≡Kn (Kn=0,1,2)
Kn=0のときは操作不要。

初期状態から、クリックされたAnの回数に対して(3-Kn)回ずつ順不同でクリックすれば、初期状態に戻すことが可能です。

また任意の状態を初期状態に戻すことが可能だと思います。
行列の加法が成立します。

赤 ０ 緑 １ ピンク ２ で表わすとする。

例えば下記の図柄を作る場合

１００
０００
０００
１を含む行と列を除いたマス目と１のマス目をクリックすればよい。
すなわち、１，５，６，８，９のマス目をクリックすればよい。
０００
０１０
０００
同様に、１，３，５，７，９のマス目をクリックすればよい。 
０００
０００
００１
同様に、１，２，４，５，９のマス目をクリックすればよい。

上記３個の図柄で合成される下図は、

１００
０１０
００１
足し算をすればよい。
３回以上クリックするマス目は３個ずつ省く。また順不同なので、
　１，５，６，８，９，１，３，５，７，９，１，２，４，５，９
＝１，１，１，２，３，４，５，５，５，６，７，８，９，９，９
＝２，３，４，６，７，８
２００
０００
０００
　１，５，６，８，９，１，５，６，８，９
＝１，１，５，５，６，６，８，８，９，９
このようにして任意の図柄を作ることが出来る。
任意の図柄を作ることが出来るので、それを初期状態に戻すことは可能である。

【おまけ２】

赤 ０ 緑 １ ピンク ２ とする。
a1,a2,a3,a4,a5,a6,a7,a8,a9 は、０，１，２とする。

任意の図柄を 

a1 a2 a3
a4 a5 a6
a7 a8 a9
とする。 この図柄を作るための操作

１→a1+a5+a6+a8+a9≡b1 (mod 3)
２→a2+a4+a6+a7+a9≡b2 (mod 3)
３→a3+a4+a5+a7+a8≡b3 (mod 3)
４→a4+a2+a3+a8+a9≡b4 (mod 3)
５→a5+a1+a3+a7+a9≡b5 (mod 3)
６→a6+a1+a2+a7+a8≡b6 (mod 3)
７→a7+a2+a3+a5+a6≡b7 (mod 3)
８→a8+a1+a3+a4+a6≡b8 (mod 3)
９→a9+a1+a2+a4+a5≡b9 (mod 3)

bn≠0 (n=1-9) のときnのマス目をbn回クリックすると上記の図柄が出来る。
初期状態に戻すためには、
bn≠0 のときnのマス目を(3-bn)回クリックすればよい。

bn≠0 (n=1-9) のとき最小の回数は、
mini=n
Σ
k=1		(3-bk)

以上です。
ポイントは行列の加法が成り立つことですね。

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる