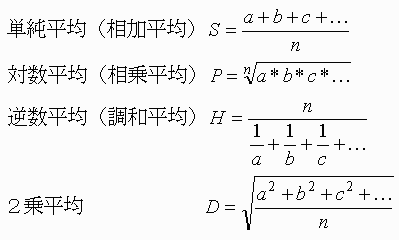
といったところでしょうか。
(名前は、n*f(平均)=f(a)+f(b)+… のf()に何を使うかから来ている様ですネ)
平均といっても色々ありますが、代表的なのは、nを変数の個数として、
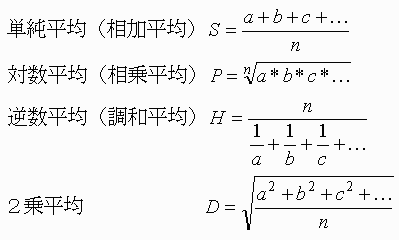
といったところでしょうか。
(名前は、n*f(平均)=f(a)+f(b)+… のf()に何を使うかから来ている様ですネ)
【問題1】
変数と単純平均、対数平均、逆数平均が全て整数の組み合わせを1つ見つけてください。
ただし、a,b,…は自然数で、変数全部が同じではない(いくつか同じでもよい)、とします。
(初めは変数が2つから試した方が無難です)
【問題2】
問題1の変数と平均は1組見つかれば"定数倍"しても成り立ちます。
そこで、単純な"定数倍"は別にして、問題1を満たす変数の関数(媒介変数表示というのかな?)を作ってください。
(変数の個数も任意の方が好ましい)
【問題3】
変数と4つの平均が全て整数の組み合わせを1つ見つけてください。
【問題4】
同様に、単純な"定数倍"は別にして、問題3を満たす変数の関数を作ってください。
(私はこれについて、変数の個数が4つの場合(それもイマイチなやつ)しか見つけられませんでした)
◆数・数列の性質へもどる
 数学の部屋へもどる
数学の部屋へもどる