図にしてみたら、合っているような気がするのですが・・・？◆千葉県 なのはな子 さんからの解答。
【問題３】
太郎 106才
次郎 98才
1+0+6=7
7X14=98
98+8=106
【問題４】
A-Bの距離は、５kmである。
38-(25+24)=-11
43-(27+11)=5
【問題５−１】
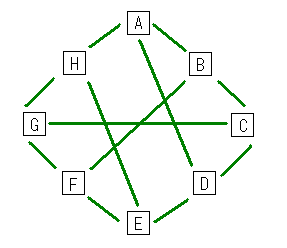
空国には、最大で９つの空港がある。
９つの空港を、Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ ，Ｈ，Ｉ とする。
・Ａ⇔Ｂ⇔Ｃ⇔Ｄ⇔Ｅ⇔Ｆ⇔Ｇ⇔Ｈ⇔Ｉ⇔Ａ（各空港共通）
・Ａ⇔Ｄ、Ａ⇔Ｇ
・Ｂ⇔Ｅ、Ｂ⇔Ｈ
・Ｃ⇔Ｆ、Ｃ⇔Ｉ
・Ｄ⇔Ｇ、Ｄ⇔Ａ
・Ｅ⇔Ｈ、Ｅ⇔Ｂ
・Ｆ⇔Ｉ、Ｆ⇔Ｃ
・Ｇ⇔Ａ、Ｇ⇔Ｄ
・Ｈ⇔Ｂ、Ｈ⇔Ｅ
・Ｉ⇔Ｃ、Ｉ⇔Ｆ
【問題５−２】
最大で、24空港ある。
◆山梨県 Footmark さんからの解答。
【問題１】
６桁の数は２6(＝６４)で割り切れるので、
当然２5,２4,２3,２2,２1でも割り切れる筈です。
また、各桁の数字は１か２です。
そこで、？が１か２であることを考慮しつつ以下のように求めます。
100の桁の数字を？とすると、
[ ?] が２1(= 2)で割り切れる筈なので、
？は２。（□□□□□２）
101の桁の数字を？とすると、
[ ?2] が２2(= 4)で割り切れる筈なので、
？は１。（□□□□１２）
102の桁の数字を？とすると、
[ ?12] が２3(= 8)で割り切れる筈なので、
？は１。（□□□１１２）
103の桁の数字を？とすると、
[ ?112] が２4(=16)で割り切れる筈なので、
？は２。（□□２１１２）
104の桁の数字を？とすると、
[ ?2112] が２5(=32)で割り切れる筈なので、
？は２。（□２２１１２）
105の桁の数字を？とすると、
[?22112] が２6(=64)で割り切れる筈なので、
？は１。（１２２１１２）
【答え】 １２２１１２
【問題２】
筆算（電卓でも可能)で、√１．９９６＝１．４１２７９８６‥ を得ます。
また、１．４や１．５の２乗では４桁になりません。
そこで、３桁からはじめ、より正確な値に前後から近づいていきます。
１．４１ ｘ１．４１ ＝１．９８８１ ダメ １．４２ ｘ１．４２ ＝２．０１６４ ダメ １．４１２ｘ１．４１２＝１．９９３７４４ ダメ １．４１３ｘ１．４１３＝１．９９６５６９ ＯＫ答えは自然数なので小数点は無視します。
【答え】 １４１３
【問題３】
次郎の年齢は１４ｎ(ｎは自然数)の筈です。
ですから、次郎の年齢を１４,２８,４２,‥と順に増やしてみれば得られます。
（年齢なので増やす回数もそんなに多い筈はありません。）
この方が、代数で解くよりはるかに早いです。
ｎ＝７のとき、条件を満たします。
【答え】 太郎：１０６歳 , 次郎：９８歳
【問題４】
(PQ)でP-Q間の距離を表すものとします。
(AB)
=[{(AF)-(CF)}+(CH)]-{(BE)+(EH)}
=[{43-25}+38]+{27+24}
=5
（A-D＝２８km も D-G＝２２km も必要なかったですね。）
【答え】 ５km
【問題５】
逆に、空港数を与え直行便の数を問えば『必要な通訳者』と一緒です。
【問題５−１】
【答え】 ７空港
【問題５−２】
【答え】 １５空港
◆広島県 清川 育男 さんからの解答。
【問題１】
６４の倍数であるためには４の倍数でなければならない。
４の倍数は下２桁が４で割り切れなければならない。
したがって、下２桁は１２。
６４の倍数であるためには８の倍数でなければならない。
８の倍数は下３桁が８で割り切れなければならない。
したがって、下３桁は１１２。
候補となる数は、（１６(5)、３２(6)と絞ってもいいが、、、） １１１１１２
１１２１１２
１２１１１２
１２２１１２ ○
２１１１１２
２１２１１２
２２１１１２
２２２１１２
以上８通りであるが題意を満たすのは、１２２１１２だけ。
【問題２】
１４の２乗は、１９６。
１４Ｘ Ｘは自然数。
Ｘ＝１３のとき、１４１３の２乗は、１９９６５６９になり、
Ｘ＝１〜１２のなかにないから、題意を満たす。
【問題３】次郎君 太郎君
１４ ２２
２８ ３６
４２ ４８
５６ ６４
７０ ７８
８４ ９２
９８ １０６ ○
【問題４】
与えられた数字をあてはめていくと、
A-5-B-13-C-10-D-4-E-11-F-7-G-6-Hとなる。
したがって、 A-Bの距離は、5km。
◆千葉県 なのはな子 さんからの解答。
【問題５】
Footmark さんの、『必要な通訳者』といっしょだという解答を見て、なるほどと思
いました。
それでやり直してみたのですが、なぜか【問題５−１】の答えが８つになりました。
図にしてみたら、合っているような気がするのですが・・・？
同じようにして考えると、【問題５−２】は19になってしまいました。・・・？
◆山梨県 Footmark さんからの解答。
【問題５】 修正版
空港数＝３ｘ(直行便数ー１)＋２＝３ｘ(直行便数)ー１ の関係になります。
直行便数が２：◎○××○
直行便数が３：◎○××○××○
直行便数が４：◎○××○××○××○
↓
ただし、左端の◎と右端の○は隣同士にあり、全体で輪になっています。
また、◎は自空港、○は直行便がある空港、×は直行便がない空港 です。
【問題５−１】
空港数＝３ｘ３ー１＝８
【答え】 ８空港
【問題５−２】
空港数＝３ｘ７ー１＝２０
【答え】 ２０空港
◆千葉県 なのはな子 さんからの解答。
【問題５−２】
１９というのは間違いでした。
「１８空港」では・・・？
計算ではFootmarkさんのいわれるとおり20空港のはずなのに・・・。
自空港(◎)の両隣の「直行便がある空港(○)」と、その次の「直行便がある空港(○)」との間は、「直行便がない空港(×)」は１つでなければ、この問題は解けないみたいです。
理由がわかりません。
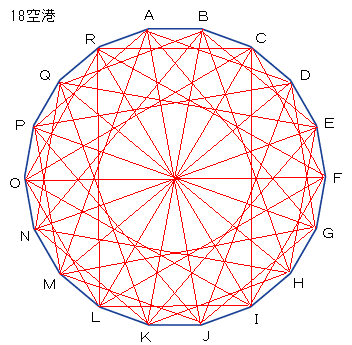
直行便数が７:◎○×○××○××○××○××○×○
空港数＝３ｘ７−３＝18
図にしてみました。
この図では、どこへでも問題の指示のとおりに行けます。
◆山梨県 Footmark さんからの解答。
【問題５】
この問題は面白いだけでなく、奥も深そうですね。
１８空港が可能なのは、なのはな子さんの図より一目瞭然です。
[ ２０空港でも可能である証明 ]
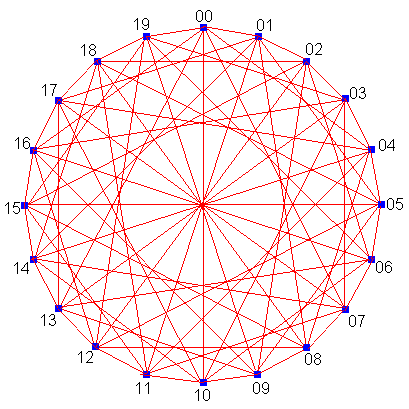
自空港を00とし、残り１９空港を時計回りに01,02,‥,19とします。
自空港から直行便で行ける空港は、表で横に並んでいる下線付き青字の７空港です。
下線付き青字の各空港で乗り換え後に行ける空港は、表でその下に縦に並んでいる各７空港です。
２０空港(00〜19)のいずれも、この５６(＝７ｘ８)の「行き先」のどこかに必ず存在します。
ですから、各空港とも示したような７航路にすると、直行便か１回の乗り換えだけですべての空港へ行くことができます。
証明終わり。
[ P・S ]
表の青字の３行に注目すると、その３行に２０空港(00〜19)のいずれも含まれています。
ですから、乗り換え後はその空港からの直行便は７航路も必要なく、前後の空港行きの２航路さえあれば十分です。
だとすると、何か無駄があるような気がします。
ひょっとすると、空港数はさらに増やすことが可能なのでしょうか？
２０空港でも可能であることは示しましたが、２０空港が最多である証明はできていません。^^；
諸兄の解答に期待したいところです。
◆出題者のコメント。
皆さん『問題５』以外は全問正解です。
『問題５』がまだ誰も正解していないみたいなので、ヒントを出します。
直行便で行ける場所は３カ所、直行便で行った場所からはそれぞれ（戻れないので）最高で２カ所です。
◆宮城県 甘泉法師 さんからの解答。
【問題５−１】
下図の空港(1)の都合だけ考えると空港の数は最大で10。
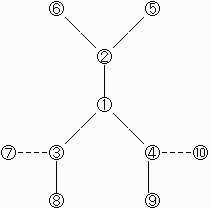
(5)と(10)、(6)と(7)、(8)と(9)、
(6)と(9)、(5)と(8)、(7)と(10)
をそれぞれ結べば題意を満たす。
答え 空港の数は１０
◆広島県 清川 育男 さんからの解答。
【問題５】
規則性から N2+1 が推理されます。
【問題５−１】
N=3
32+1=10
【問題５−２】
N=7
72+1=50
【青木コメント】
どうも清川さん予想が正しいようです。
◆大阪府 ゆたか さんからのコメント。
【問題１】について、次のような応用問題が考えられます。
【問題２】について、次のような類題が考えられます。
◆山梨県 Footmark さんからの解答。
【問題１】の応用問題
最上位桁の数字は０でないものとする。
【問題１】の応用問題１
各桁の数字が１か２であるN(≧1)桁の数をS(N)とし、
その内で２Nで割り切れるものをT(N)とする。
k(≧1)桁の時、T(k)が存在すると仮定する。
∴ T(k)≡０ (mod ２k)
また、ある数で割り切れるが、ある数の２倍で割り切れないなら、そのときの余りはある数である。
∴ T(k)≡０ (mod ２k+1) あるいは T(k)≡２k (mod ２k+1)
そこで、
S(k+1)＝ｐ*１０k＋T(k)＝ｐ*５k*２k＋T(k)＝ｑ*２k＋T(k) とする。
（ただし、ｐは１桁の正整数でｑは正整数）
●T(k)≡０ (mod ２k+1) のとき
ｑを偶数にすると、
S(k+1)＝ｑ*２k＋T(k)≡(ｑ/２)*２k+1＋０≡０ (mod ２k+1)
ｑを奇数にすると、
S(k+1)＝ｑ*２k＋T(k)≡ｑ*２k＋０≡２k(mod ２k+1)
●T(k)≡２k (mod ２k+1)のとき
ｑを奇数にすると、
S(k+1)＝ｑ*２k＋T(k)≡２k＋２k≡０ (mod ２k+1)
ｑを偶数にすると、
| S(K+1)＝ｑ*２k＋T(k)≡ | ｑ ２ | *２k+1＋２k≡２k (mod ２k+1) |
明らかにｐとｑの偶奇は等しいので、
T(k)≡０ (mod ２k+1) のときは、ｐが偶数であるときに限りT(k+1)が存在する。
T(k)≡２k (mod ２k+1) のときは、ｐが奇数であるときに限りT(k+1)が存在する。
ところが、ｐは１(唯一の奇数)か２(唯一の偶数)なので、T(k+1)は唯１つしか存在しない。
以上より、T(k)が存在するなら、T(k+1)は唯１つだが存在する。
ところで、２1で割り切れるS(1)は、T(1)＝２ の唯１つだけである。
よって、すべてのNに対してT(N)は唯１つ存在する。
証明終わり。
[ P・S ]
この証明からも解るように【問題１】の解法には以下もあります。
１位の桁の数字は明らかに偶数２、よって□□□□□２を得ます。
そこで、２を４で割ってみます。
割り切れないので１つ上の桁は奇数１、よって□□□□１２を得ます。
そこで、１２を８で割ってみます。
割り切れないので１つ上の桁は奇数１、よって□□□１１２を得ます。
そこで、１１２を１６で割ってみます。
割り切れるので１つ上の桁は偶数２、よって□□２１１２を得ます。
そこで、２１１２を３２で割ってみます。
割り切れるので１つ上の桁は偶数２、よって□２２１１２を得ます。
そこで、２２１１２を６４で割ってみます。
割り切れないので１つ上の桁は奇数１、よって１２２１１２を得ます。
【問題１】の応用問題２
問題文の表現「各桁の数字がａかｂのＮ桁の数」は、片方の数字だけの使用でもよいものとする。
また、特にａ≠ｂの条件もないので、ａ＝ｂも許すものとする。
各桁の数字がａかｂであるN(≧1)桁の数で、２Nで割り切れるものをT(N)とする。
また、同じ構成数字で唯一つしか存在しないT(N)をU(N)とする。
U(1)＝2,4,6,8
U(2)＝12,16,20,24,28,32,36,40,44,52,56,60,64,68,72,76,80,88,92,96
（48と84は同じ構成数字なので除く）
ここで、T(3)を考えてみる。
よって、U(3)はU(2)の内で構成数字が０以外の２種類の偶数であるものを除いてから得なければならない。
U(3)＝112,616,200,232,336,400,144,344,544,744,944,552,656,600,272,776,800,288,488,688,888,992,696
U(4)も同様に、U(3)の内で構成数字が０以外の２種類の偶数であるものを除いてから得なければならない。
U(4)＝2112,1616,2000,3232,6336,4000,4144,3344,4544,7744,4944,5552,6656,6000,2272,7776,8000,1888,3888,5888,7888,9888,2992,9696
ここで、いずれのU(4)も２種類の数字で構成されているが、２種類とも０以外の偶数であるものはない。
よって、各U(N)における許される構成要素a,bは以下である。
(0≦a≦b≦9)
U(１)のとき、
一方の数字＝2,4,6,8
他方の数字＝任意１桁数
(ただし、他方の数字は構成数字として使用しない)
U(２)のとき、
a＝0,0,0,0,1,1,2,2,2,2,2,2,3,4,4,5,6,6,6,8
b＝2,4,6,8,2,6,3,4,5,7,8,9,6,4,6,6,7,8,9,8
(ただし、片方の数字だけの使用なら、4と4は4と任意１桁数、8と8は8と任意１桁数)
U(３)のとき、
a＝0,0,0,0,1,1,1,2,2,2,2,2,3,3,4,4,4,4,5,6,6,6,8
b＝2,4,6,8,2,4,6,3,5,7,8,9,4,6,5,7,8,9,6,7,8,9,8
(ただし、片方の数字だけの使用なら、8と8は8と任意１桁数)
U(N)(N≧４)のとき、
a＝0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,4,4,4,5,5,6,6,7,8
b＝2,4,6,8,2,4,6,8,3,5,7,9,4,6,8,5,7,9,6,8,7,9,8,9
(0と2,4,6,8とのペア４組と、2,4,6,8と1,3,5,7,9とのペア２０組の計２４組)
[ P・S ]
N≧４ の条件付きなら、構成数字は２種類(ａ≠ｂ)ないと不可能なので、もっとスッキリしたのですが・・。
【問題２】の応用問題１
２度目なので、より正確に表現します。
筆算（電卓でも可能)で、√１．９９８＝１．４１３５ と有効桁数５桁までを得ます。
有効桁数の関係から、１．４１３５ の末尾の数字に１を加えた
１．４１３６ の２乗は必ず １．９９８・・ となります。
ただし、最小値とは限りません。
そこで最小値を得るため、末尾の数字に１を加えた有効桁数２桁〜５桁を、順に確かめてみます。
１．５ｘ１．５＝２．２５
１．４２ｘ１．４２＝２．０１６４
１．４１４ｘ１．４１４＝１．９９９３９６
１．４１３６ｘ１．４１３６＝１．９９８２６４９６
許される最大桁の １．４１３６ が最小値であることが確認できます。
よって、求める最小な自然数は １４１３６ です。
【問題２】の応用問題２
AをN(≧1)桁の自然数としても、一般性を失うことはありません。
有効桁数の関係から、(N+1)桁の自然数
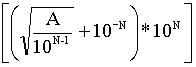は必ず条件を満たします。
（ただし、[ ]はガウス記号）
よって、任意のＮ桁の任意な自然数Ａに対して、２乗すると頭のＮ桁がＡとなる自然数が必ず存在します。
【問題２】の応用問題の補足問題
（１） 真の値の有効桁数を順に増やしてみて確かめるとき、何故末尾の数字に１を加えてから確かめるのでしょうか？
（２）(N+1)桁の自然数
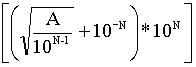を２乗すると、何故頭のN桁が自然数Aになるのでしょうか？
ただし、[ ]はガウス記号。
◆大阪府 ゆたか さんからのコメント。
早々の解答ありがとうございます。
【問題１】の応用問題
（１）
正解です。おまけに、私の考えていた【問題１】の解法も示していただき恐縮です。
Footmarkさんは帰納法で簡潔に証明してくれましたが、もうひとつ用意していた証明があります。
それは、「各桁の数字が１か２のＮ桁の数は全部で２N個ありますが、それら各々を２Nで割った余りはすべて異なる。」ことを証明するという方法です。
この証明にも挑戦してみてください。
（２）
問題文の表現が少し曖昧だったようです。
文頭に「任意のＮに対して」を追加するとよりスッキリすると思います。
この場合、FootmarkさんのＮ≧４の場合の解が正解であると思われます。
【問題２】の応用問題
（１）
残念ながらもっと小さい数が存在します。
一見【問題２】と変わらない問題ですが解法に落とし穴があります。
（２）
具体例を示していただきました。
これで、最小値を求める問題が意味を持ちますね。
◆山梨県 Footmark さんからの解答。
【問題２】の応用問題１
もう１つの場合を吟味するのを忘れていました。^^;
互いに１０の奇数乗倍同士の２つの場合を確認する必要があります。
(１０の偶数乗倍はすべて同一の数字の並びになるので必要ありません)
√１．９９８からの最小値は、前に示したように１４１３６。
そこで、√１９.９８からの最小値も求めてみます。
筆算（電卓でも可能)で、√１９.９８＝４．４６９８ と有効桁数５桁までを得ます。
有効桁数の関係から、４．４６９８ の末尾の数字に１を加えた
４．４６９９ の２乗は必ず １９．９８・・ となります。
ただし、最小値とは限りません。
そこで最小値を得るため、末尾の数字に１を加えた有効桁数２桁〜５桁を、順に確かめてみます。
４．５ｘ４．５＝２０．２５
４．４７ｘ４．４７＝１９．９８０９
４．４７ が最小値であることが確認できます。
(自然数なら４４７)
明らかに、４４７＜１４１３６。
よって、求める最小な自然数は ４４７ です。
【答え】 ４４７
◆東京都 鳳 奥人 さんからの解答。
【問題１】
各桁の数字が１か２である６桁の数は単純計算で６４（２6）通り。
６４の倍数ということは１の位は絶対偶数なので、３２通り。
この３２通りを全部はじきだして、６４で割ってみる・・・という力技もありますが、そういう類の問題ではないですよね（笑）
この３２通りのうち最小の数は111112。
これを64で割った余りは８です。
また、100000、10000、1000、100、10を64で割った余りはそれぞれ32, 16, 40, 36, 10 です。
求める数は、111112に100000, 10000, 1000, 100, 10をそれぞれ１回または０回足した数です。
それぞれの余り同士を足した数が、64の倍数になっていれば、元の数の和も64の倍数です。
例）
(64a+42)+(64b+22) = 64(a+b)+64 = 64(a+b+1)
(64c+57)+(64d+38)+(64e+33)
= 64(c+d+e)+128
= 64(c+d+e+2)
余り同士の和が64になるのは 8+16+40
（111112の余り８は絶対に必要）
このとき元の数は
111112+10000+1000=122112
余り同士の和が128になるのは・・・ないようです。
（余り同士をすべて足すと142。ここから14を引けばいいのですが、自分自身が14であるものも、足して14になる組み合わせもありません）
余り同士の和が192以上ということは当然ありえません。
というわけで、求める数は122112です。
【問題２】
1996X の形では不可。
(1412＝19881、1422＝20164）
1996XX の形でも不可。
（4462＝198916、4472＝199806）
1996XXXの形では 14132が1996569。
これが最小です。
（ちなみに14122は1993744です）
【問題３】
常識的に考えて、太郎君の年齢は100歳未満とします。
太郎君の年齢を(10a+b)歳とすると
（a, bとも０以上９以下の整数）、
次郎君の年齢は(10a+b-8)歳。
また、次郎君の発言より次郎君の年齢は14(a+b)歳と書けます。
よって10a+b-8 = 14(a+b)
したがって4a+13b= -8
・・・おや？ａもｂも０以上だと成り立ちません。
ひょっとして太郎君の年齢は１００歳超えてるんでしょうか。
とすると、太郎君の年齢は100+10a+b
次郎君の年齢は92+10a+b、かつ14(1+a+b)
だから92+10a+b＝14(1+a+b)
したがって4a+13b＝78
これならいけそうです。
b＝(78-4a)/13
これを満たすａ・ｂの組み合わせは ａ＝０、ｂ＝６
というわけで太郎君は106歳。次郎君は98歳です。
確かに条件は満たしていますけど「君」なんていう年齢ではないですねぇ・・・。
【問題４】
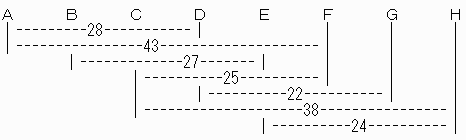
これより
ＤＦ＝ＡＦ−ＡＤ＝１５
ＣＥ＝ＣＨ−ＥＨ＝１４
ＦＨ＝ＣＨ−ＣＦ＝１３
ＥＦ＝ＣＦ−ＣＥ＝１１
ＢＣ＝ＢＥ−ＣＥ＝１３
ＦＧ＝ＤＧ−ＤＦ＝７
ＤＥ＝ＤＦ−ＥＦ＝４
ＧＨ＝ＦＨ−ＦＧ＝６
ＣＤ＝ＣＥ−ＤＥ＝１０
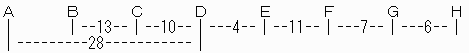
よって、ＡＢ＝ＡＤ−（ＢＣ＋ＣＤ）＝５
答え：５ｋｍ
◆神奈川県 ココちゃん さんからの解答。
【問題４】
ある鉄道の線路に、下り方向に向かってA.B.C.D.E.F.G.Hという８つの駅があるので
A-D＝２８km、A-F＝４３km、B-E＝２７km、C-F＝２５km、
D-G＝２２km、C-H＝３８km、E-H＝２４km より
A--D ＝２８km
D--G ＝２２km G=50
A----F ＝４３km
C--F ＝２５km A-C=18
C----H＝３８km A------H=56
E--H＝２４km A---E=32
B--E ＝２７km AB=5となるので５kmです。◆宮城県 甘泉法師 さんからのコメント。
【問題５−２】
直行便がＮ路線出ているとして最大の空港の数がN2+1 との予想があり、
Ｎ＝1,2,3については成り立ち、つなぎ方がわかっていますが、N=4のつなぎかたがわかりません。
この予想は正しいのでしょうか。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題５ ◆宮城県 甘泉法師 さんからのコメント。】
【解答】 予想は正しくありません。
ＰＣで虱潰しに調べたところ、１７空港は不可能で１５空港が最大でした。
１５空港の場合であれば、Ｎ＝３の唯一解を重複させる解があります。
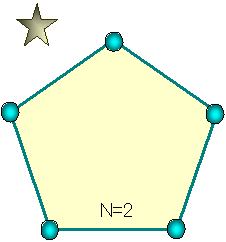
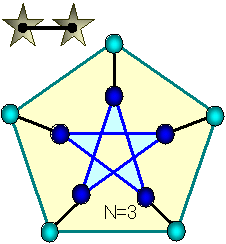
下図Ｎ＝３参照。
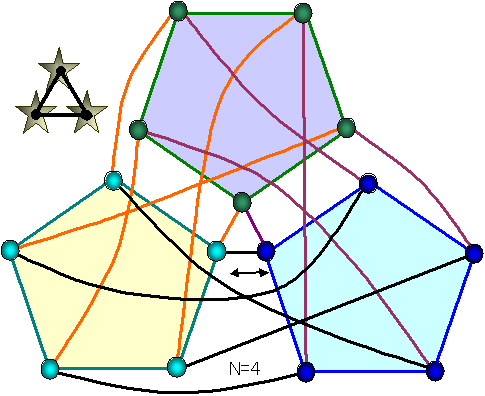
これらは５角形が基本になっており、
ここから 最大空港数の予想＝５×（Ｎ−１） が得られかつ、それは可能です。
下図参照。
黒線は 上図Ｎ＝３の黒線５航路をまとめたベクトルです。
また金星は５空港とこれを循環する５航路です。
しかし、この予想は最大ではないようです。
最初の図のＮ＝４の図の←→で示す航路は緑の空港経由で代用できます。
従って、緑のような金星が５個以上あれば 青グループとシアングループ間の航路は不要になります。
この関係を最大限無駄なく利用できるＮを考えるとそれはＮ＝７であって、このとき５０空港が可能です。
つまりＮ＝７では清川さんの予想どおりとなります。
（下図参照、航路は１セットのみ描画。）
具体的には金星１０グループを赤組５☆、緑組５☆にわけ、各組間は航路を設けず、相手組空港を経由して自分組空港と結びます。
５が素数であるため、そのような設定を全ての空港間に対して実現可能です。
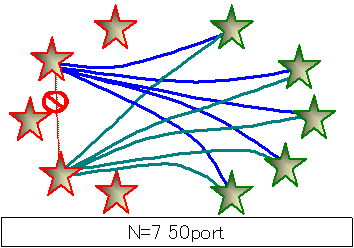
【プログラムの考え方】
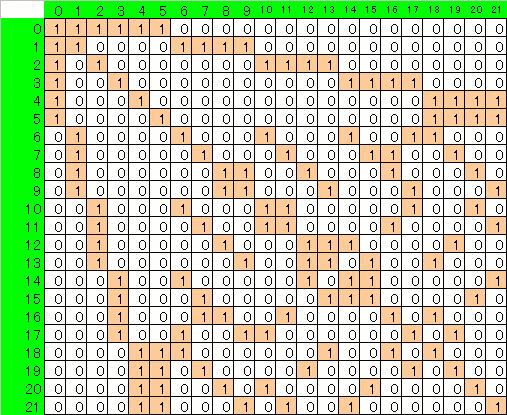
空港間の航路の有無を行列 Ａ であらわすこととします。
ここで Ａ（ｉ，ｊ）はｉ空港とｊ空港間に航路があるとき１、ないとき０という値をとります。
また Ａ（ｉ，i）=1とします。
従ってＡは 対称で、対角成分が全て１、各行ないし列の和がＮ＋１である行列です。
題意を満たす Ａは Ａ２の各成分が正であるもとなります。
下記はＮ＝７ 空港数５０に対応するＡとＡ２です。
絵をクリックすると大きくなります。
| Ａ Ｎ＝７ Ｐｏｒｔ＝５０ | Ａ２ |
|---|---|
 |
 |
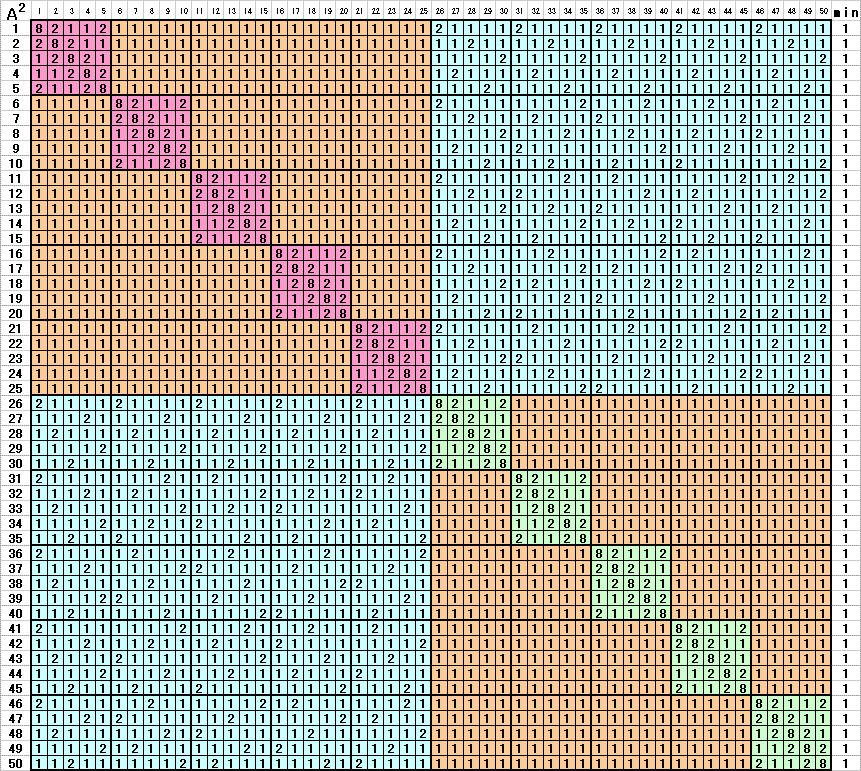【感想】
かなり面白く深い問題です。
Ｎ＝４は虱潰しできましたが Ｎ＝５、６はかなり工夫しないとＰＣでは無理みたいです。
何とか Ｎ＝５ の 場合の最大値をＰＣで見つけたいですね。
２６より少ないと推定されます。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題５ 解答続編】
N=5の場合に関しPCで探索ができました。
最大は２４空港でした。
下図に対応する行列Aと実際のつなぎ方を示します。
このパターンしかないようです。
| 行列 N=5 空港＝２４ | 経路図 |
|---|---|
 |
 |
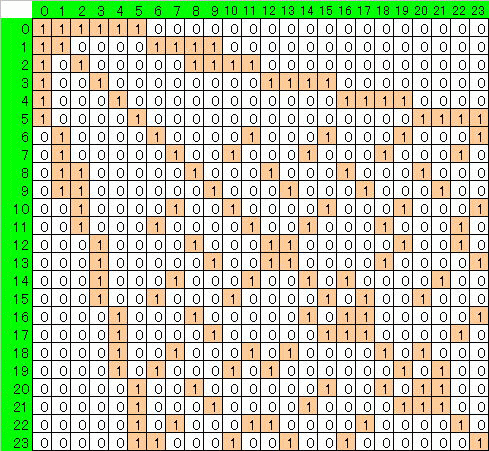【探索方法 概要】
空港数＝２６の場合
対称性を考慮して経路の必須パターンを考慮すると下図が得られ、０番から９番までのつなぎ方が決定できる。
したがって、残り１６空港からの経路をPCにより虱潰し探索したところ解はなかった。
なお、６，７，８，９番からの経路がこのように定まるのは、１番と１０番以降の１６空港をつなぐにはこの経路パターンしかないからである。
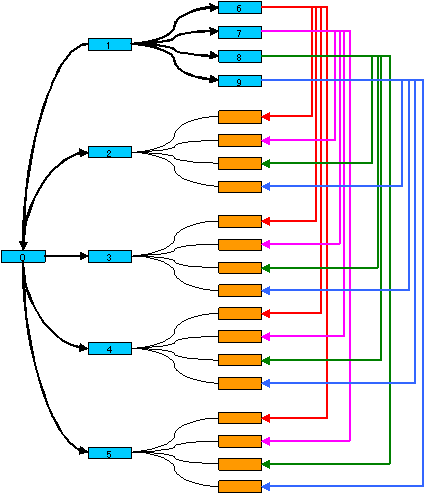
空港数＝２５,２３，２１の場合
奇数空港数の場合、５×奇数は奇数であり、４方向しか使えない空港が１空港発生する。
これを０番空港とする。
このとき、０番から接続可能な空港の数は最大２１である。
すなわち、空港数２５，２３はできない。
２１空港の場合、対称性を考慮して経路の必須パターンを考慮すると下図が得られ、０番から4番までのつなぎ方が決定できる。
５番から８番の残りの各１方向と、９番以降の１２空港からの経路をPCにより虱潰し探索したところ解は多数合った。
即ち２１空港は可能である。
具体的な経路は、空港数＝２２の解の５番空港をはずしたもの等がある。
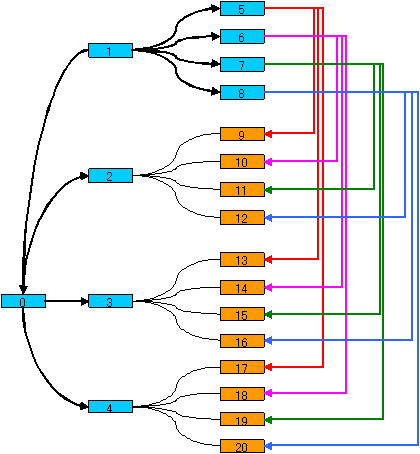
空港数＝２４の場合
対称性を考慮して経路の必須パターンを考慮すると下図の一部が得られる。
さらに、１番空港からの経路のうち２方向が８番と９番に接続する場合を設定し、必須経路を考慮すると下図が得られる。
そして残りの部分をPCにより虱潰し探索すると、解答の経路が得られた。
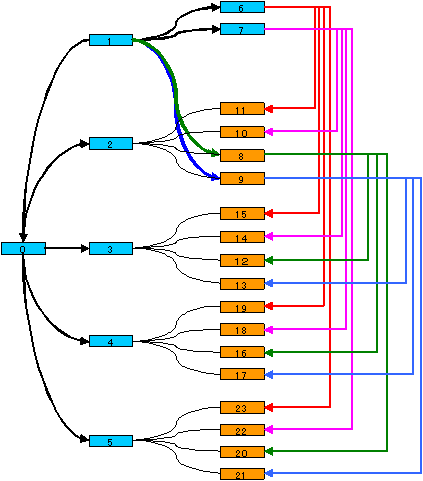
空港数＝２２の場合
下図に示すように、２２空港も可能である。
他にもう１パターンあることを確認しているが、それ以上は探索していない。
４番空港と同一なつながり方をしている５番空港をはずすことで、２１空港の経路にもなる。
| 行列 N=5 空港＝２２ | 経路図 |
|---|---|
 |
 |
◆広島県 清川 育男 さんからのコメント。
Y.M.Ojisan さんの解答から数列サイトを検索して一般項を推理してみました。
| m=[ | n+1 2 | ]， [ ]はガウスの記号とする。 |
| A(n)=3*2m+2*m-6+(2m+1)* | 1+(-1)n 2 |
2 5 10 15 24 33 50 67 100 133 198 263 392 521 778 1035 1548 2061 3086 4111
階差数列は興味深い数列のようです。
3, 5 , 5 , 9 , 9 , 17 ,17, 33 , 33 , 65 , 65 ,129 ,129 , 257 ,257 , 513 , 513 ,1025 ,1025
2n+1