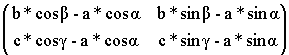
◆宮城県 アンパンマン さんからの解答。
(未完成な)解答です。
【問題１】
12時の位置から進んだ秒針の角度＝θとする。
(針の回転方向＝正の角度)
| 長針の角度＝ | θ 60 |
| 短針の角度＝ | θ 3600 |
定理
原点から三つの線(長さa,b,c)がある。
線の先端の位置をA、B、Cとする。
三つの線とある軸との角度はα、β、γとすると△ABCの面積は
| 1 2 | |ab sin(α-β)+bc sin(β-γ)+ca sin(γ-α)|である。 |
| 定理より、ν＝ | 59θ 3600 |
とすると |
| 三つの針の先端でできた面積は | 1 2 | |f(ν)|で、 |
f(ν)＝-ab sin(ν)-bc sin(60ν)+ca sin(61ν)です。
面積が最大になるときは
f'(ν)＝0、つまりνが
61ca cos(61ν)-60bc cos(60ν)-ab cos(ν)=0 の解の中です。
求めたνが
| S＝ | 1 2 | |ab sin(ν)+bc sin(60ν)+ca sin(61ν)| |
を最大にさせる値でしたら面積が最大の時のνになります。
| そのとき、秒針が | 3600ν 59 |
の角度で進みました。 |
すなわち、短針が
| 3600ν 59 |
* | 60 2π*3600 |
＝ | 30ν 59π |
時間を進みました。 |
【問題２】
f'(ν)＝0からνが
61cos(61ν)-60cos(60ν)-cos(ν)=0の式を満たします。
ν＝?
◆東京都 You.O さんからの解答。
【問題２】
数値解法でないと解けないみたいですね。
Excelで解いた結果です。
３つの針の長さをａ、午前０時からｔ分後における、針の先を頂点とする三角形の面積をＳとする。
このとき、長針、短針、秒針がこの順に時計回りにある場合と反時計回りにある場合に分けて考えると、
Ｓ＝｜sin(5.5°×ｔ)＋sin(354°×ｔ)－sin(359.5°×ｔ)｜×a2
となることがわかる。
１秒単位では午前／午後５時４９分９秒，午前／午後６時１０分５１秒に
ｍａｘ（Ｓ）≒１．２９８９５５８×ａ2 となります。
時計が完全なアナログ時計だとすると、
午前／午後２時５４分３４秒５６，午前／午後９時５分２５秒４４のあたりで
ｍａｘ（Ｓ）≒１．２９９０３５３×ａ2
となります。
午前０時から午前６時までの間で面積が大きくなる１秒単位の時刻ベスト１１とそのときの面積、および長針と短針、長針と秒針、短針と秒針がなす小さいほうの角の大きさを次の表に掲げました。
これを見るとやはり、３つの針の先を頂点とする三角形が正三角形に近いとき、面積が最大となることがわかります。
Excelの解析結果から、約１３０２秒（２１分４２秒）ごとに面積が最大に近づき、この時刻の前後１秒ごと、１分ごとにも面積が最大に近づくことがわかりました。
| 順位 | 時刻 | Ｓ／ａ2 | 長針と短針の なす角（°） | 長針と秒針の なす角（°） | 短針と秒針の なす角（°） |
| １ | 5:49'09" | 1.298955803 | 120.325 | 119.1 | 120.575 |
| ２ | 3:37'58" | 1.298879196 | 118.8167 | 120.2 | 120.9833 |
| ３ | 2:32'53" | 1.298796432 | 120.8583 | 120.7 | 118.4417 |
| ４ | 0:21'42" | 1.298710252 | 119.35 | 121.8 | 118.85 |
| ５ | 3:59'40" | 1.298550436 | 121.8333 | 118 | 120.1667 |
| ６ | 4:44'04" | 1.29840438 | 122.3667 | 119.6 | 118.0333 |
| ７ | 1:26'47" | 1.298317956 | 117.3083 | 121.3 | 121.3917 |
| ８ | 1:49'29" | 1.298143185 | 117.8417 | 122.9 | 119.2583 |
| ９ | 2:54'35" | 1.298140379 | 119.7917 | 117.5 | 122.7083 |
| １０ | 5:05'46" | 1.298079012 | 118.2833 | 118.6 | 123.1167 |
| １１ | 0:43'24" | 1.297716212 | 121.3 | 116.4 | 122.3 |
◆宮城県 甘泉法師 さんからの解答。
【問題１】
ふつうの角度の符号のとりかたにあわせるため時計を横に寝かせ裏から見た0時0分0秒からのt秒経過後の角度のラジアンは
| α= | 2πt 60*60*12 |
，β= | 2πt 60*60 |
，γ= | 2πt 60 |
よってγ=720α β=12α
時計の軸を中心にしたｘｙ座標で
短針先端の座標（a*cosα, a*sinα）
長針先端の座標（b*cosβ, b*sinβ）
秒針先端の座標（c*cosγ, c*sinγ）
△ABCの面積を|S|として2Sは、下の行列の行列式.
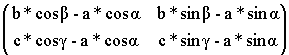
よって、
2S=(b*cosβ-a*cosα)(c*sinγ-a*sinα)-(c*cosγ-a*cosα)(b*sinβ-a*sinα) =ab*sin(β-α)+bc*sin(γ-β)+ca*sin(α-γ) =ab*sin(11α)+ bc*sin(708α)+ca*sin(-719α)両辺をαで微分すると
| d dα |
2S=11ab*cos(11α)+708bc*cos(708α)-719ca*cos(719α) |
極値をとるαは多数ある。
|S|の最大値がどれかは実地に調べる必要がある。
面積の最大値を陽にa,b,cであらわすことは難しい。
【問題２】
a=b=c=p の場合は
2S=p2{sin(11α)+sin(708α)-sin(719α)}
| d dα |
2S=p2{11cos(11α)+708cos(708α)-719cos(719α)} |
| 理想の配置、各針間の角度が１２０度で面積が | 3 4 |
* p2 は |
| ｜sin(11α)｜＝｜sin(708α)｜＝｜sin(719α)｜= | 2 |
だが、これを満足するαはおそらくない。
たとえば４時ちょうどと８時ちょうどは、短針と長針は１２０度で理想的だが秒針の位置はよろしくない。
秒針の位置があう ３時５９分４０秒くらい と ８時００分２０秒くらいでは長針と短針の間は１２０度からわずかだがずれている。
| 面積最大値の候補のαは長針と短針が角度 | 2π 3 | をなす |
α0= |
11 |
α0= |
11 |
の近傍で、秒針がその前後を１周する間
| |α-α0| 2π |
＜ | 1 720 |
このような候補は、短針が1周する半日のうちに22回ある。
【コメント】
異なる22個のα0を初期値にして微分が０になる方程式の解を求めるプログラムを組み極大値を求める。
これらのうち最大のものが面積最大値になるはずです。
上に引いた４時、８時の場合の具合から考えてその間、5時50分少し前と６時10分少し後が、最大面積を与えるのでないかと予想します。
◆東京都 ぽこぺん さんからの解答。
【問題２】
[1]
短針，長針，秒針の長さを共に a とし，0時0分0秒からの秒数をtとする。
t の範囲は 0≦t≦43200 (＝12×60×60) で考えればよい。
3つの針の先で作られる三角形の面積は
| a2 2 | * | sin( | 1 3600 | - | 1 60 | )*2πt + sin( | 1 43200 | - | 1 3600 | )*2πt+ sin( | 1 60 | - | 1 43200 | )*2πt | |
f(t) ＝ - sin780αt - sin11αt + sin719αt
となる。
| ただし，α ＝ | 2π 43200 | とする。 |
なお，
f(43200 - t)
＝ - sin(780×2π - 780αt) - sin(11×2π - 11αt) + sin(719×2π - 719αt)
＝ - f(t)
| であるから，グラフは点( | 43200 2 | , 0) に関して点対称である。 |
[2]
0≦t≦43200 における f(t) の零点は
(1) 秒針が長針と重なる t
| t ＝ | 3600n 59 | (0≦n≦708) |
(2) 長針が短針と重なる t
| t ＝ | 43200n 11 | (0≦n≦11) |
(3) 短針が秒針と重なる t
| t ＝ | 43200n 719 | (0≦n≦719) |
の合計 2 + 707 + 10 + 718 = 1437 個あり，区間の両端では(1)～(3)が一致する。
また，両端の2点を除き，(1)と(2)を合わせた717個は，(3)の718個と交互に出現する。
これを大きさの順に並べて {an} (n＝0, 1, ...1436) とする。
（添付の表 Zero_and_Maxの第1列）
[3]
f(t) を t について微分すると
f’(t) ＝ α(- 780cos780αt - 11cos11αt + 719cos719αt)
となる。
この各零点は f(t) の隣り合う零点の間にちょうど1個ずつ存在することが数値的に検証できるから
（添付の表 f’(t) のグラフ），f(t)は各 an の間に1個ずつ極値を持つ。
そこで，f'(t) の零点を大きさの順に並べて {bn} (n＝0, 1, ..., 1435)とし，
an と a(n+1) の平均を初期値としてNewton法を用いて bn の近似値を求めると，添付の表 Zero_and_Max の第4列のようになる。
ただし，計算はMathematicaを用いて20桁の精度（内部30桁，表示20桁）で実行した。
（他の全数値の計算も同様）
[4]
各 bn に対して f(bn) を求め，点(x, f(x)) (x = a0, b0, a1, b1, ...)
のグラフを描くと添付の表 Envelope のようになる。
この包絡線の図から明らかなように，f(t) の極値 f(bn) のうち正の側の11個，負の側の11個を比較すればよい。
それぞれの極値の絶対値を取り，f(t) の対称性に注意して極値を与えるt の値の時分秒表示を求めると，添付の表 Result のようになる。
極値の大きさの順に並べると，次のとおりである：
1.299035307108 2:54:34.56 9:05:25.44 1.299026920892 5:49:09.12 6:10:50.88 1.298993291031 0:21:41.75 11:38:18.25 1.298968260779 2:32:52.81 9:27:07.19 1.298900747204 3:37:58.07 8:22:01.93 1.298859458084 0:43:23.51 11:16:36.49 1.298757553113 5:05:45.62 6:54:14.38 1.298700647030 3:59:39.82 8:00:20.18 1.298563589204 1:49:29.30 10:10:30.70 1.298491964739 4:44:03.86 7:15:56.14 1.298318738891 1:26:47.01 10:33:12.99したがって，この1行目が三角形の面積の最大値を与える。