
◆山梨県 Footmark さんからの解答。
【問題2】
円に内接する正三角形,正四角形,正六角形は誰もが周知なので省略する。
円に内接する正五角形なら、以下に示す極めてシンプルな作図法で可能である。

与えられた円Oの1つの直径をABとし、それに直交する直径をPQとする。
OAを直径とする円O’を描き、直線PO’との交点をTとする。
Pを中心に半径PTの円を描き、円Oとの交点をそれぞれX,Yとする。
すると、線分XYは円Oに内接する正五角形の1辺である。
後はXYのコンパス幅で円Oの円周を5分割し、得られた5交点の隣同士を直線で結べばよい。
[ 証明 ]
与えられた円Oを単位円(半径=1)とすると、
| PO’=√{1+( | 1 2 | ) | 2 | } | = | 2 |
| = | 2 | − | 1 2 |
| = | 2 |
| ∴ XM:XQ=PX:PQ= | 2 | :2 |
| ∴ XY:XQ= |
1+ 2 |
証明は終わり。
[ P・S ]
問題には「円に内接する・・」とあります。
どんな正n角形でも必ず円に内接しますから、題意は「与えられた円に内接する・・」の意味だと思います。
ですから、お二人が示されている「1辺が与えられた時の作図法」では、題意を満たしていないのでは・・。
◆埼玉県の中学校2年生 太公BOW☆ さんからの解答。
【問題4】
定規とコンパスだけで正7角形を書く。
偶然みつけました。
【コメント】
これって本当に1%程度ですか。
どなたか確認して下さい。
◆大阪府 ふにゃふむ さんからの解答。
【問題1】
これは重心の性質を使うと解けますね。
ある線分をABとします。
まずAを中心に円を描きます。
そしてAを通る直線を引き、先ほどの円との2つの交点をM、Nとしておきます。
さらにMとB、NとBをそれぞれ線分で結んでおきます。
そしてBNもしくはBMに垂直2等分線を引き、円との交点をPとします。
三角形BNMにおいてPと反対側にある頂点を結ぶとABと交わり、この点がこの三角形の重心となります。
重心は線分を2:1に分けるので、あとは比が2である方に垂直ニ等分線を引けば、三等分した事になりますね。
これで問題解決です!
ふと思ったのですが、何故重心は線分を2対1に分けるのでしょうか?
う〜ん…謎です。

◆岡山県 えりくん さんからの解答。
【問題1】
まず、3等分する直線を線分ABとする。
その線分を一辺とする正三角形を作る。
さらに、その正三角形の外接円をかく。
その外接円の円の中心で対称になるような正三角形を作る。
(ここで円に外接する星形ができてるはず。)
星形ができたときには、はじめの線分ABは三等分されているのではないでしょうか。

◆千葉県 なのはな子 さんからの解答。
【問題1】
コンパスは長さを測るだけ、定規は直線を引くだけです。
これで3等分できると思うのですが、どうでしょう?

【コメント】
Gは△CBDの重心ですからできていますね。
◆北海道 小西 さんからの解答。
正17角形の作図法を書いている解答が見あたらなかったので、ご存じの方もいると思いますが紹介します。
ガウスの功績によると

です。
平方根が作図できますから手順は掛かりますが正17角形は作図可能です。
より簡単な方法として以下のリッチモンドの方法が知られています。
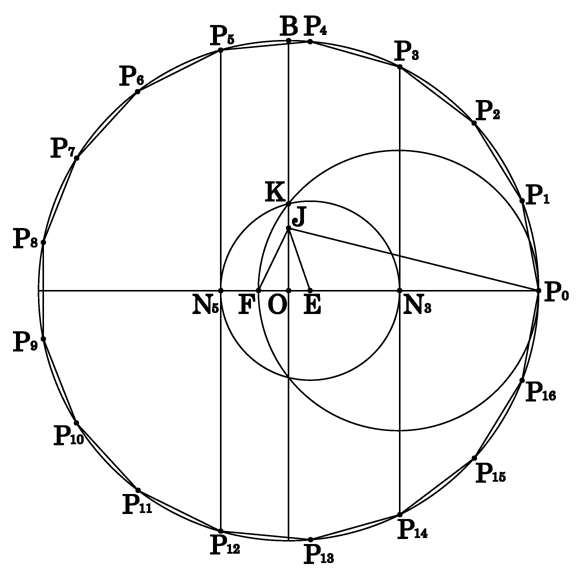
図において, OからBへ至る4分の1の点Jと P0とを結びます。
P0を通る直径上にE, Fをとり, 角OJEが角OJP0の4分の1,
FJEが45度になるようにします。
FP0を直径とする円を描き, OBとの交点をKとします。
中心をE, 半径をEKとする円を作り,
OP0とN3(OとP0との間にある), N5で交わるとします。
これら2点からOP0に垂線を立て, 上側の半円との交点をそれぞれP3, P5とします。
このとき弧P0P3, P3P5はそれぞれ円周全体の3/17, 2/17となります。
[参考文献]
Simon G. Gindikin 著, 三浦 伸夫 訳, "ガウスが切り開いた道",
シュプリンガー・フェアラーク東京株式会社, (1996)
◆滋賀県 とある大学生 さんからの解答。
【問題2】
36度が作図できれば事足りる。
そのために頂角が36度、斜辺(?)が1の二等辺三角形を考えると、
| 底辺が黄金比で有名な | −1+ 2 |
となるので、 |
説明を簡単にするためにX−Y座標軸を考えることにする。
| 単位円を取って、O(0,0)、A(1,0)、B(0, | 1 2 |
)を取ると、 |
| AB= | 2 |
。 |
点Bを中心にOBの長さを半径にもつ円を描き、その円と線分ABとの交点をCとすると、
| CB= | −1+ 2 |
。 |
このCBを半径に、中心をBに取り円を描く。
この円と単位円Oとの2交点をD、Eとすると線分DEが正5角形の1辺となる。
残りの辺は書くまでも無いが、コンパスでDEの長さを取って、それぞれD,Eを中心に円を描き、単位円Oとのそれぞれの交点とD,Eを結び、最後 にそれらの交点と点(-1,0)とを結べば終了。
最後に、愛知県の高校生 あんでぃ〜 さんはなかなか鋭い目を持っていますね。
実は「定規とコンパスのみで作図」することと拡大体の概念が同値のようなんですが、あまり詳しい事を説明する能力を欠いているのでこの辺で止めて
おきます。
(まぁ誰かが補足してくださるだろうと期待して・・)
◆東京都 ぽこぺん さんからのコメント。
●[埼玉県の中学校2年生 太公BOW☆ さんからの解答]に関するコメント
円の半径を 1 とすると,
| ・本方法による一辺の長さ: | 7 8 |
= 0.875 |
| ・真の値:2sin | π 7 |
= 0.867767… |
ですから,相対誤差は約 0.8 %となります。
| 2sin | π 7 |
= 0.867767478235116… を連分数展開すると, |

となるので,その第 n 近似分数は
| n | 近似分数 | 相対誤差 |
| 1 | 1 | --- |
| 2 | 6/7 | 1.2% |
| 3 | 7/8 | 0.8% |
| 4 | 13/15 | 0.1% |
| 5 | 46/53 | 0.02% |
| … |
のようになります。7/8 は作図も簡単だし,コロンブスの卵のような非常に単純な近似法であり,優れている と思います。
なお,13/15 であれば,半径の 1/3 と 1/5 の差 2/15 を除いた残りということで,こちらも簡単に作図できます。
◆東京都 ぽこぺん さんからの解答。
太公BOW☆さんの方法にヒントを得て,
| 2sin | π 17 |
= 0.3674990356331406631… |

となるので,その第 n 近似分数は
| n | 近似分数 | 相対誤差 |
| 1 | 1/2 | --- |
| 2 | 1/3 | 9.2% |
| 3 | 3/8 | 2.0% |
| 4 | 4/11 | 1.0% |
| 5 | 7/19 | 0.25% |
| 6 | 18/49 | 0.04% |
| … |
となります。
| ここで, | 18 49 |
= (2 + | 4 7 |
) / 7 ですから, |
| (直径+半径の | 4 7 |
)を 7 等分するだけで求まります。 |
※なんでこんな簡単な方法に今まで気づかなかったのだろう???
【追加問題5】
あまり知られていないようですが,正十五角形は定規とコンパスで作図できるでしょうか?
作図できるならばその手順を示し,できないならばそれを証明してください。
◆神奈川県の中学校3年生 ヒロポン さんからの解答。
【問題1】
点Aから上に適当に直線を引き、Pと置きます。
AC=CD=DEとなるような点を直線P上に作る。
BとEを結びます。
線分BEと平行になるような直線を点D、点C から引き、ABとの交点を点F,点Gと置きます。
すると、三角形の中点連結定理が成り立って、AF=FG=GBとなります。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題5】
代数的に解くと下記が得られ、平方根ばかりなので作図可能です。
![]()
具体的には、正5角形を作図し、その外接円に内接し頂点を共有する
正3角形を5個描けば可能です。
正3角を一個描き5角形との間をコンパスでとって15回継ぎ足す方法も可能で、作図は容易です。
このように互いに素な因数の正多角形が全て作図可能なら、その積の正多角形も作図可能です。
◆熊本県の中学校2年生 維盛 さんからの解答。
【問題5】
円Oに内接する正十五角形があり、ひとつの頂点をA、その隣の頂点をBとした際の∠AOBは、
360÷15=24
故に、24°となります。
つまり、24°が作図できれば、正十五角形の作図も可能です。
作図方法
◆兵庫県 quax! さんからの解答。
【問題4】
正7角形の近似図形
誤差は約0.2%でちょっと大きめですが、作図が簡単なので書いてみました。
◆愛知県 迷子の雄猫 さんからの解答。
【問題1】
線分ABを定規とコンパスだけを使って3等分してください。
Aを通り角CABが45度くらいになる直線ACをひく。
AC上に、Aから等間隔になるように点C1、C2、C3をとる。
C3Bと平行でC1、C2を通るような直線と、線分ABの交点をB1、B2とする。
【問題2】
円Sに内接する、正三,四,五,六角形の、「定規とコンパス」だけを用いた作図方法を考えてください。
円Sの直径をひく。
(適当な弦の垂直2等分線をひく。)
円Sとの交点をA,Cとする。
その直径ACの垂直2等分線をひく。
円Sとの交点をB,D、直径AC,BDの交点をoとする。
-->四角形ABCDが正四角形になる。
点A,Cを中心として点oを通る円Sa、Scを書く。
-->円S,Sa、Scの交点と点A,Cを順に結ぶと正6角形、ひとつおきに結ぶと正3角形になる。