点Ｇ，Ｈが求める３等分点です。
◆岩手県 浮浪ぱなしさんからの解答。
【問題１】の解答
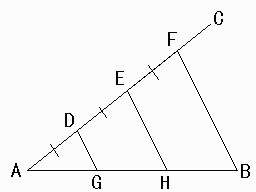
(1)適当に半直線ＡＣをかく
(2)半直線ＡＣ上に，コンパスでＡＤ＝ＤＥ＝ＥＦとなるような点Ｄ,Ｅ,Ｆをとる。
(3)点Ｄを通る直線ＢＦに平行な直線と線分ＡＢとの交点をＧとする
(4)点Ｅを通る直線ＢＦに平行な直線と線分ＡＢとの交点をＨとする
点Ｇ，Ｈが求める３等分点です。
【コメント】
確かに、３等分点になりますが、平行線を引くのはどうなのでしょうか？
定規とコンパスで可能でしょうが、とばしてよいのでしょうか。
【出題者の清川さんのコメント】
歴史的な作図の問題の条件（詳細はよく知りませんが）からは、外れていると思いますが、日常的には、２つの三角定規を使って一方を固定して、他方をスライドさせ、平行線を引くことがありますし、三角定規の個数が、規定されていないので、正解でいいのではないでしょうか。
私の思いはこのようなものでした。
青木先生は厳密な方法をご存じなのでしょうね。
◆東京都 Ｙ．Ｍさんからの解答。
[問題１解答]
図が書けないので、明らかな操作は省略します。
一応、この方法では何等分でもできます。
(1) 適当な方向に点Ａを通る直線を引く。
(2) 点Bを通り、かつ(1)に平行な線を引く。
(3) (1)で書いた点Ａを通る平行線上に点Ａから(コンパスで)適当な長さをとり印をつける。(点Ａ'とする)
(4) (2)で書いた点Ｂを通る平行線上に点Ｂから(3)とは逆方向に(3)の２倍の長さの点をとり印をつける。(点Ｂ'とする)
(5)点Ａ'と点Ｂ'を結ぶ。この時線分ＡＢは１：２となる。
◆東京都 Ｙ．Ｍさんからの解答。
[問題２解答?]
正３、４、５、６角形などは円の半径と正多角形の一辺の比が四則演算と根号で表せるので作図可能です。
図が送れないので具体的な方法は省略します。
.... これでは解答になっていない(^_^;)
一方、正７、９角形などは作図不可能です。
ちなみに「初等整数論」(高木 著...絶版)という本に正１７角形の作図方法が載っています。
【コメント】
正１７角形の作図は有名ですが、すごいですねぇー。
正５角形の作図が難しいのではないかと思っているのですが、どうでしょうか。
古代ギリシャ人は知っていたそうですが。
◆広島県 清川さんからの解答。
【問題２】
正５角形の作図
正５角形の頂点を反時計回りにABCDEとする。
まず辺ＣＤをきめる。
辺ＣＤの垂直２等分線を引く（これは可能）。
辺ＣＤとの交点をＸとする。
点Ｘから上方へ辺ＣＤの長さをとりその点をＹとする。
ＣＹの延長線上にＣＸ＝ＹＺとなる点Ｚを決める。
点Ｃを中心に半径ＣＺの円を描き、辺ＣＤの垂直２等分線との上方での交点をＡとする。
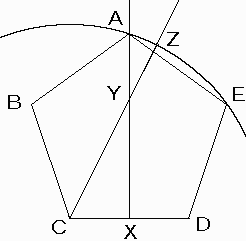
点Ａと点Ｃから点Ｂを左側にきめる。
点Ａと点Ｄから点Ｅを右側にきめる。
一辺の長さは、ＣＤ。
（１＋
）／２を決定することがポイントですね。
中学時代に技術家庭科の製図の実習で習った記憶があります。
当時、意味はよく解りませんでした。
指示通りに描いただけでした。
正１７角形について触れてありましたが、若きガウスがフェルマー型の素数（２n＋１）に限ることを証明したとのことですね。
正Ｎ角形（Ｎが素数のとき）。
現在までに解っているフェルマー型素数 ２n＋１＝３，５，１７，２５７，６５５３７。
そこで、質問があります。
正２５７角形、正６５５３７角形も作図可能なのでしょうか。
◆京都府の大学院生 わかさひ君からの解答。
『定規とコンパスを使って・・・』の話ですが、平行線は、定規とコンパスだけで作図できます。
答えは…と書くとつまらないので、問題にしてみてください。
問題：ある直線Ｌと一点Ａがあるとき、Ａを通ってＬに平行な直線を作図せよ
それだけでは物足りないので、問題１の別の解法を書いておきます。
線分ＡＢを３倍します。これをＡＣとします。
ＡＢ＝ＡＤとなるようにＤをとります。(ただし、直線ＡＢ上に存在しないこと)
直線ＡＤと点Ｄで接し、なおかつ点Ｃを通るような円Ｏを作図します。
# この作図法を問題にしても良さそうですね。
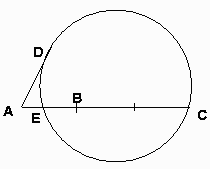
円ＯはなぜかＡＢの間を通るんですが、この交点をＥとすると、これが求める三等分点になります。
（３ＡＥ＝ＡＢ)
# どうしてこれでいいのかを証明するのは…中学生にはちょうど良い問題かも。
問題２は知っている人間が答えてもつまらないので止めておきますね。
理論的には２５７角形と６５５３７角形が書けるんですけど…けどねぇ…(^^;
# ところで、初等整数論講義(高木貞治)は改版(復刻と言うのかな)されて出ていたような…今度本屋に行った時にでも調べてみます。
#確かこの本に『角度の問題』の話も出ていたような…。
◆広島県 清川さんからの解答。
わかさひ君さんの宿題
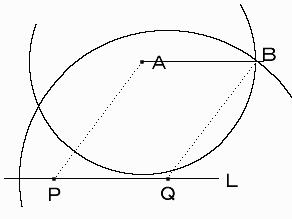
１）点Ａから直線Ｌに垂線を引き、その足を点Ｂとする。
直線Ｌ上に点Ｃをとり、点Ｃを通り直線Ｌに垂直な直線を引く。
点Ａの側にＡＢ＝ＣＤとなる点Ｄを決める。
点Ａ、点Ｄを通る直線を直線Ｍとする。
直線Ｍは直線Ｌに平行な直線となる。
２）点Ｄを通り線分ＡＤに垂直な直線を引き、また線分ＤＣの垂直２等分線との交点を点Ｏとする。
点Ｏが求める円の中心となる。
点Ｏを中心に半径ＤＯの円を描き、線分ＡＣとの交点を点Ｅとする。
△ＥＡＤと△ＤＡＣにおいて、
∠ＥＤＡ＝∠ＤＣＡ。
∠ＥＡＤ＝∠ＤＡＣ。
よって△ＥＡＤと△ＤＡＣは相似な三角形となる。
ＥＡ：ＤＡ＝ＡＤ：ＡＣ
点Ｅは線分ＡＢの３等分点となる。
◆岩手県 浮浪ぱなしさんからの解答。
[わかさひ君の宿題]に対する清川さんの解答（平行線の作図）について。
もちろん正しいのですが，手順が多すぎて実用的ではありませんね。
◆筑波大学大学院 恩田さんからの解答。
【問題１】の解答
線分の３等分線の問題ですが、平行線を使わないやり方もあります。
次に、平行四辺形の辺ＡＢ、ＢＣの中点をＥ，Ｆとします。
これは、中学校２年生の教科書に「３等分されることを証明せよ」という問題で、載っていました。
【コメント】
なるほど、コロンブスの卵というか、ちょっと気がつかない方法ですね。
◆石川県 数学好き さんからの解答。
【問題１】の解答
線分ＡＢの３等分点の求め方ですが、基本的には、岩手県 浮浪ばなしさんと同じですが、平行線の引き方を次のようにします。（平行四辺形の応用）
◆東京都 eiki さんからの解答。
【問題１】線分ABをコンパスと定規だけを使って３等分してください。
【解答】
（ＡＢを１辺とする正３角形ＡＢＤを描き、ＢＤの中点をＭとすれば、角ＢＡＭは３０度になります。
【補足】
この方法はｎ等分に拡張して使えますが、答としてはつまらない。
◆東京都 eiki さんからの解答。
正五角形の作図について
線分ＡＢの中点をＯとし、ＡＢを直径とする（すなわち中心をＯとする）円を描きます。
Ｎを通りＯＢと垂直な直線と、最初の円との交点をＦとすると、線分ＯＡと線分ＯＦは正５角形の隣接する２辺になります。
あとは、ＯＡの垂直２等分線とＯＦの垂直２等分線との交点Ｇを求め、Ｇを中心として半径ＯＧの円を描けば、それが正５角形の外接円ですから、
◆東京都 eiki さんからの解答。
【近似的な正７角形の作図】
１．線分ＡＢの中点をＯとし、線分ＡＢを直径とする半円を描きます。
あとは、ＯＡの垂直２等分線とＯＥの垂直２等分線との交点Ｆを求め、Ｆを中心として半径ＯＦの円を描けば、それが正７角形の外接円ですから、ＯＡの長さの弦を描いていけばおしまい。
実はこの方法、正７角形に限らず、同じ手順（注）で正ｎ角形が描けるのです。
（注） 上記手順３の内分点Ｄを（ｎ−２）：２とすること
なお、ＯＣ／ＯＡ＝１２／７にしたほうが精度は高いのですが、正７角形以外では手順がやや面倒になるので、ＯＣ／ＯＡ＝
◆東京都 eiki さんからの解答。
【定規とコンパスを使って。。。の補足】
正多角形の作図について誤差を計算してみました。
（誤差は２辺のなす角に着目しています）
ついでに。。。
【コメント】
実際に定規とコンパスで書くとすれば、簡単に書けるということが最も大切なことなので、この程度の誤差なら充分だと思います。
◆宮城県 斉藤 誠さんからの解答。
【問題１】の解答
直線の３等分点を、３角形の重心を使って作図してみました。
１、線分ＡＢを１辺とする正３角形をつくる
２、角ＡＢＣの２等分線を引くと、１で引いた垂直２等分線との交点Ｏが重心になる。
３、辺ＡＣに平行で点Ｏを通る直線と辺ＡＢとの交点Ｐが線分ＡＢの３等分点になる。
コンパスの幅を替えずに作図したかったのですが、最後のＯＢから垂線を引くところはコンパスの幅を広げざるを得ないのでしょうか、ちょっと思いつきません。
◆静岡県 ヨッシーさんからの解答。
【問題１】のみの解答です。（他のは入り込む余地がなさそうなので）
まずは、やり方から、
(1)線分ＡＢの端点Ａから、適当な線分ＡＣを引き、ＡＣの中点を作図し、Ｄとします。
上記の記号を使うと、
が常に成り立つ、というのがメネラウスの定理（中学生でも証明可）です。
この場合、
ですから、
ＦはＡＢを２：１に内分する点となります。
いろんな比率に内分する点を作図することが出来ます。
◆大阪府の高校生 ＣＨＥＣＫ さんからの解答。
【問題１】の解答
１．作図方法
２．証明
線分ＡＥとＢＤは△ＡＢＣの中線であり、その交点である点Ｇは△ＡＢＣの重心である。
∴ＡＧ：ＧＥ＝ＢＧ：ＧＤ＝２：１
同様にＢＥとＱＧが平行なので
よってＡＰ：ＰＱ：ＱＢ＝１：１：１となり、２点Ｐ，ＱはＡＢを３等分する。
◆東京都 小室 英正 さんからの解答。
【問題１】に対する解答です。
・操作
△ＡＣＤにおいて、２辺ＡＣ、ＣＤの中点がＥ、Ｂである。
感想
ただ線分を３等分するだけなのに、ずいぶんといろいろな方法があるものですね。
◆滋賀県 一平ちゃん さんからの解答。
【問題１解答】
ＡからＢ方向以外に半直線ＡＸを引く。
◆新潟県 mack さんからの解答。
【問題１】
線分ABをコンパスと定規だけを使って３等分してください。
（１）まず、点Bから線分ABと同一直線にならないように適当に直線を引きます。
次に、点A、C、Dを結び三角形を作ります。
点CとF、DとEを結び、その交点をGと置く。
すると、AG：GB＝2：1となります。
（２）点Aにおいても、同様の操作を行うことにより
以上において求めた２点より線分ABを３等分することが出来ます。
◆愛知県の高校生 あんでぃ〜 さんからのコメント。
問題２の<疑問点>で、思ったことをひとつ。
“定規”は直線y=ax+bを描く。
“コンパス”は円 x2+y2=r2を描く。
直線と円（または直線同士、円同士）が交わったところは連立方程式の解になる。
ここで、複素数αn=1を考える。
2次方程式は、解の公式から3乗根、4乗根などは出てこない。
逆に、整数、分数、√などだけで解が構成されてれば、それは作図可能である。
これはあくまで単位円周上の話だが、定規とコンパスで長さを定数倍することは可能なので、この相似形も作図できるだろう。
何の証明にもなってないけど、これらのことから作図可、不可が少しはわかるんじゃないでしょうか。
◆東京都 鷹宮 さんからの解答。
【問題１】
線分ABを定規とコンパスだけを使って３等分してください。
解答
実は、これと同じやり方で線分をｎ等分できます。
やり方は上に書いたものとほぼ同じですが、
証明
三角形ＡＦＤと、三角形ＧＤＡは相似です。
ちなみに、コンパスと定規を使って作図できる図形はコンパスのみでも作図できる（モールの定理）のですが、あいにく参考図書が見つからない為、証明の仕方分かりません。
とりあえず、この問題はコンパスのみで作図できます。
『１』で直線を引かず、『２』に進みます。
３回目で、ちょうど１８０度ですから、Ｃが作図できます。
その後は同じ手順で作画していき、
『７』で描いた円との２つの交点のうち、１つはＡですが、もう一つの点がＧです。
『８』の代わりに、６行上に書いたやり方で
以上です。
◆宮城県 甘泉法師 さんからの解答。
【問題１】の解答
正三角形の重心を使います。
線分の同じ端点から左右それぞれに角度３０度の直線を引きます。
◆山梨県 Footmark さんからの解答。
【問題１】
「三角形の角の二等分線は、対辺が他の２辺の比で内分される点を通る」
この作図法だと、３等分に限らず線分を［１：有理数］に内分することも可能です。
以下は線分ＡＢの３等分点の作図法です。
（図の線分ＡＯは敢えて書く必要はありません）
●まずは、ＡＯ：ＢＯの比が １：２ になる任意の点Ｏを求めます。
［名もない定理］より、ＡＱ：ＢＱ＝ＡＯ：ＢＯ＝１：２ ですから、
［名もない定理の証明］
△ＡＢＣの頂点Ｃを通る辺ＡＢに平行な直線を引きます。
△ＰＡＢと△ＰＱＣは相似なので、
ところで線分ＡＱは∠Ａの二等分線なので、
∴ ∠ＰＡＣ＝∠ＰＱＣ
すると、△ＣＡＱは二等辺三角形で ＱＣ＝ＡＣ
∴ ＰＢ：ＰＣ＝ＡＢ：ＱＣ＝ＡＢ：ＡＣ
証明は終わりです。
◆宮城県 甘泉法師 さんからの解答。
【問題４】
●円に内接する正ｎ角形の近似的作図について
正ｎ角形の中心と隣り合う頂点を結ぶ線分どうしのなす角
明らかに、２πから次々に角を２等分していくことにより
相対誤差の表
【感想】
工夫がなさ過ぎる気はしています。
【問題３】
正方形ABCDがある。
◆宮城県 甘泉法師 さんからのコメント。
【正９角形を折り紙でつくること】
http://www.nikonet.or.jp/spring/origami/origami.htmから引用
コンパスと定規では任意の角を三等分することはできませんが、折り紙では実現できます。
図を使った説明もあります。
【問題３へのコメント】
できた長さ1/3の辺をつかって同様に比 1：3の相似三角形をつくり長さ1/4を得る
◆千葉県の中学校３年生 小八兵衛 さんからの解答。
【問題１】の解答
要は、線分ＡＢを中線とする三角形を作図すればいいわけです。
<作図> その円とＡＢの交点をＦ’とすると、ＦとＦ’がそれぞれ線分ＡＢを三等分する点になります。
ＥＡ＝ＡＥ
ＤＡ＝ＡＤ＝ＡＢ
ＡＣ＝３ＡＢ
ＡＥ：ＡＢ＝１：３
次のような手順の方が良いのではないかと思います。
1)直線Ｌ上に任意の２つの点Ｐ，Ｑを取る。
2)点Ｑを中心として線分ＰＡの長さを半径とする円（実際は弧）をかく。
3)点Ａを中心として線分ＰＱの長さを半径とする円（実際は弧）をかく。
4)上記，２つの円（弧）の交点をＢとし，直線ＡＢ（これが平行線）をかく。
~~~~＼
もちろん，点Ａと同じ側の交点
長方形を利用して作図するのか，平行四辺形を利用して作図するのかの違いですけどね。(^^;)
ＡＣを３等分する線分とします。
ＡＣを対角線とする平行四辺形ＡＢＣＤを作図します。
これは、ＡＣの中点を作図し、その中点を通り、ＡＣに垂直な直線を引き、中点を中心とする任意半径の円を描けば、作図することができます。
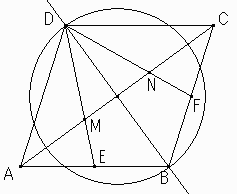
頂点Ｄからこれらの点Ｅ，Ｆの直線を引けば、その直線と対角線ＡＣの交点は３等分線になります。
はじめてみたときは、ちょっと感心してしまいました。
しかし教科書に載っているとは全く知りませんでした。
私はめったに教科書を見ない方なので？！。
ＦＢ＝ＥＧ、ＦＥ＝ＢＧ（つまり、平行四辺形ＦＢＧＥを作る）となるように、コンパスで点Ｇを求める。
ＡＢとＥＧの交点をＩとする。
同様に ＥＧ＝ＤＨ、ＥＤ＝ＧＨとなる点Ｈを求める。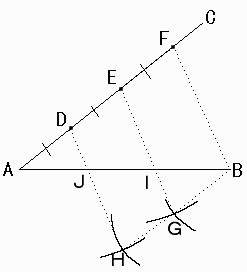
ＡＢとＤＨの交点をＪとする。
（または、線分ＡＩの垂直二等分線とＡＩの交点をＪとしてもよい。）
ゆえに、点Ｉ，Ｊは３等分点となる。
角ＡＢＣが直角、角ＢＡＣ＝３０度の直角三角形を描きます。
なお、直角や中点の作図方法は省略）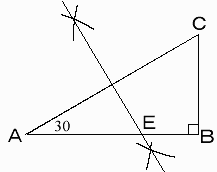
ＡＣの垂直２等分線とＡＢとの交点をＥとすると、ＥはＡＢを２：１に内分する点です。（証明略）
線分ＡＢと適当な角をなす半直線ＡＸを描き、コンパスを適当な間隔ｄに開いて、点ＡからＡＦ＝ｄとなる点ＦをＡＸ上にとり、点ＦからＦＧ＝ｄとなる点ＧをＡＸ上にとり、点ＧからＧＨ＝ｄとなる点ＨをＡＸ上にとり、ＢＨをつないで、点Ｇを通り、ＢＨと平行な直線をひけば、ＡＢとの交点がＡＢを２：１に内分する点です。
またＡＢとＯで直交する直線と円との交点をＣ、Ｄとします。
（要するに円を４等分する）
ＯＡの中点Ｍを求め、線分ＯＢ上にＥＭ＝ＣＭとなる点Ｅをとり（中心をＭとし半径ＣＭの円とＯＢとの交点がＥです）、さらにＯＥの中点Ｎを求めます。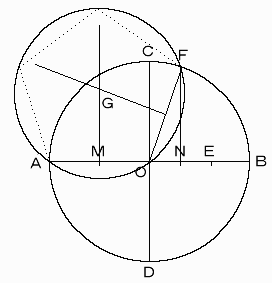
ＯＡの長さの弦を描いていけばおしまい。
２．線分ＡＢを１辺とする正３角形ＡＢＣを半円と反対側に描きます。
３．線分ＡＢを７等分し、Ｂから２つめの点をＤとします。
（Ｄは線分ＡＢを５：２に内分する点です）
４．ＣとＤを直線で結び、半円との交点Ｅを求めます。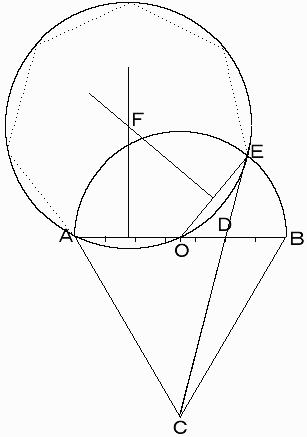
すると、線分ＯＡと線分ＯＥは正７角形の隣接する２辺になります。
実際にはｎ＝３，４，６のときしか正確な図形が描けませんし、ｎが大きくなるにつれて誤差が大きくなっていきますが、何といっても手順が簡単なのが自慢です。
で近似しました。
正５角形から正１７角形までの誤差を順に示します。
正５角形 ０．０６％ 正６角形 ０．００％ 正７角形 ０．１７％ 正８角形 ０．４２％ 正９角形 ０．６９％ 正１０角形 ０．９９％ 正１１角形 １．２９％ 正１２角形 １，５８％ 正１３角形 １．８６％ 正１４角形 ２．１４％ 正１５角形 ２．４０％ 正１６角形 ２．６５％ 正１７角形 ２．８８％
作図方法は、ｎによらずルート３で近似してしまいましたが、実際に計算してみたら ｎが大きくなると、１．５８ 程度の値になりますので、相当いいかげんな近似であることがわかりました。
まあ、シンプルであるということで、見逃してください。
正１０角形までは１％以内におさまって、特にｇｏｏｄですね。
（同時に線分ＡＢの垂直２等分線も引きます。）
線分ＡＢを半径とするコンパスで頂点Ｃ、Ｃ’を求める。
線分ＡＢの反対側の頂点Ｃ’とＣを通る直線を引く
よって、点ＯはＡＣを底辺、Ｂを頂点とする正３角形の高さの１／３の点になる。
１で使ったコンパスで頂点Ａと頂点Ｃから等距離でＡＣを軸として点Ｂと反対側に点Ｂ’をもとめ、直線ＢＢ’を引く。
平行線を引く代わりに、直線ＯＢにＯを足とする垂線を引く（手数が少ない）
この垂線と線分ＡＢとの交点Ｐが３等分点になる。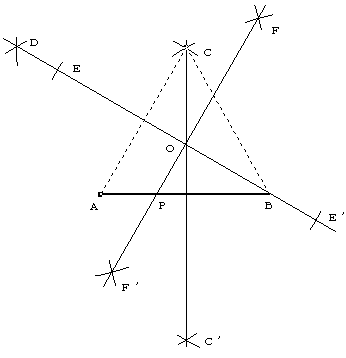
４、もう一方の３等分点をコンパスでコピーする。
作図はアルファベット順になります。
(2)線分ＢＤの中点を作図し、Ｅとします。
(3)直線ＣＥと線分ＡＢの交点Ｆが、線分ＡＢを３等分する点の１つ（Ｂに近い方）となります。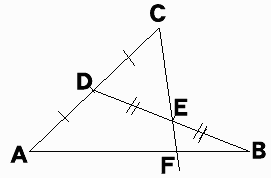
これは、メネラウスの定理を利用した方法です。
ＡＦ
ＦＢ・ ＢＥ
ＥＤ・ ＤＣ
ＣＡ＝１
ＢＥ
ＥＤ＝１、 ＤＣ
ＣＡ＝ １
２
ＡＦ
ＦＢ＝ ２
１となり、
ＤＣ
ＣＡの値は、任意に設定できますから、
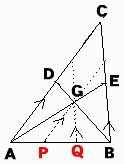
∴ＡＤとＰＧが平行なので
ＢＰ：ＰＡ＝ＢＧ：ＧＤ＝２：１
ＡＱ：ＱＢ＝ＡＧ：ＧＥ＝２：１
重心の性質を使ってみました。
平行線の作図を用いないという点で、いいかもしれません。
・簡単な証明
ただし、ＣとＤは同じ点ではないものとする。
点Ｐは中線ＡＢ、ＤＥの交点である。
三角形の中線の交点は重心であるので、点Ｐは△ＡＣＤの重心である。
重心は中線を２：１に内分するので、ＡＰ：ＰＢ＝２：１となっている。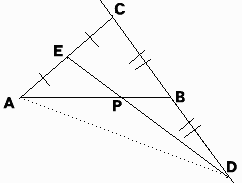
特に、教科書に載っていたという平行四辺形を利用するものと、30°60°90°の直角三角形を利用したもの、円（方べきの定理）を利用したものには驚きました。
コンパスでＡＣ＝ＣＤ＝ＤＥなる点Ｃ，Ｄ，Ｅをとる。
ＥとＢを結び、ＥＢに平行にＣＦ,ＤＧを引けば、Ｆ、Ｇが求める点である。
点Bにコンパスの軸を置き適当な大きさの円を描き、先ほどの直線と交わった２点をそれぞれC、Dとします。
線分AC、ADの中点をコンパスで求めそれぞれの点をE、Fとします。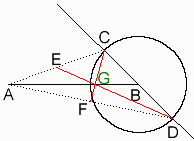
線分ABを1：2に分ける点を求めることが出来ます。
すなわち1次方程式だ。
これは2次方程式をあらわす。
てことは、“定規とコンパスでかける”ものは、2次以下の方程式およびその解だ。
この解（根）αは、複素平面上で単位円周上に存在し、その点を結ぶと正ｎ角形になる。
（証明は、あまりにも有名なので省略）
つまり、αn=1の解に、これらが含まれていれば、それは定規とコンパスでは作図できない。
（たとえば、α3=1の解は1,ω,ω2だから、正三角形は作図できる）
以上で、ＡＢの３等分点Ｇ、Ｈが求まりました。
１ヶ所はＡです。Ａではない方をＣとします。
そのＣから、半径ＡＢの円を描きます。
１ヶ所はＢです。Ｂではない方をＦとします。
（３ＡＢ＝ＡＦです。）
そのＦから、半径ＡＦの円を描きます。
この円は、ＡＢと２ヶ所で交わります。
１ヶ所はＡです。Ａではない方をＧとします。
３ＡＧ＝ＡＢです。
この円は、ＡＢと２ヶ所で交わります。
１ヶ所はＡです。Ａではない方をＨとします。
３ＧＨ＝ＡＢです。
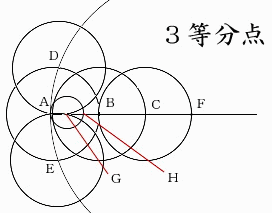
（ｎ≧２の整数）
『５』の段階でｎＡＢ＝ＡＦの点を取り、Ｆから半径ＡＦの円を描きます。
以下は同じ手順です。
最後に、『８』の手順を（ｎ−１）回繰り返してください。
それぞれ辺の比が等しい２等辺三角形（１：ｎ：ｎ）で、１つの角の大きさが同じですから。
（Ａの座標をＯとして円の交点を求める事もできますが、計算が面倒です。）
『３』のあと、『３』で描いた円をＡから半径ＡＢで３回切っていきます。
『７』のあと、Ｅを中心とした半径ＡＢの円を描きます。
2
n， 3
n...を取ります。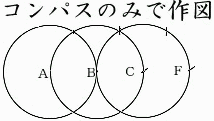 
（両側に正三角形をつくって対辺を2等分すればよい。）
別の端に直交する線をひきます。
３つの直線の作る正三角形のどちらかの角の２等分線とオリジナルな線分の交点は
線分を２：１に内分します。
これから線分を３等分できます。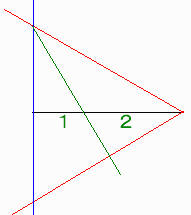
この事実を利用した作図法です。
（何と言う名前の定理なのか知らないので「名もない定理」とします）^^;
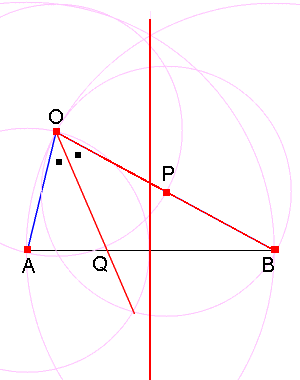
●次に、∠ＡＯＢの二等分線を引きます。
●∠ＡＯＢの二等分線と線分ＡＢの交点Ｑが求める点になります。
線分ＡＱは線分ＡＢの３分の１になります。
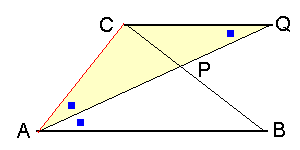
∠Ａの二等分線と辺ＢＣとの交点をＰ、引いた平行線との交点をＱとします。
ＰＢ：ＰＣ＝ＡＢ：ＱＣ , ∠ＰＡＢ＝∠ＰＱＣ
∠ＰＡＢ＝∠ＰＡＣ２π
ｎ を近似的に作図する。
２π
２mを作図することができる。
１
ｎを２進法の小数であらわして、小数点ｍ桁が１ならば、
ｍ桁まででうちきった角度でつぎつぎに中心角をあてていき、最後の一切れにくる誤差が一番大きいが、
角度に ２π
２mを加えるとすると、
これは ｆ＝ ２πｎ
２mより小さい。
相対誤差 は高々これを
２π
ｎで割った
ｎ2
２m
ｍ＼ｎ ５ １０ １５ ２０ 1 12.500 50.000 112.500 200.000 2 6.250 25.000 56.250 100.000 3 3.125 12.500 28.125 50.000 4 1.563 6.250 14.063 25.000 5 0.781 3.125 7.031 12.500 6 0.391 1.563 3.516 6.250 7 0.195 0.781 1.758 3.125 8 0.098 0.391 0.879 1.563 9 0.049 0.195 0.439 0.781 10 0.024 0.098 0.220 0.391 11 0.012 0.049 0.110 0.195 12 0.006 0.024 0.055 0.098 13 0.003 0.012 0.027 0.049 14 0.002 0.006 0.014 0.024 15 0.001 0.003 0.007 0.012
MCとBDの交点をPと名づけると
△PBCと△PDMは相似で比は２：１
このことによって、例えば正9角形を作成することができることになります。
できた長さ1/4の辺をつかって同様に比 1：4の相似三角形をつくり長さ1/5を得る
・・・・・・・・・・・
できた長さ1/ｎの辺をつかって同様に比 1：ｎの相似三角形をつくり長さ1/(n+1)を得る
・・・・・・・・・・・
このようにできた長さを任意のｍ倍することにより、折り紙で、あるいはコンパスと定規をつかって、任意の有理数の長さがえられることがわかります。
まず、点Ｂを通る直線を書きます。
次に、コンパスで、点Ｂを中心とする円を書きます。
その円と直線の交点をそれぞれＣ，Ｄとします。
三点Ａ，Ｃ，Ｄを結ぶと、△ＡＣＤができます。
後は、ＡＣの中点(Ｅとする)をとり、そことＤを結びます。
そして、ＡＢとＤＥの交点をＦとして、ＡＦとＢＦのうち短いほうを半径にした円を書きます。