亖俼俠丗俻俛
亖俠俙/
 丗俠俛/
丗俠俛/
亖俠俙丗俠俛側偺偱
仧搶嫗搒丂Asami丂偝傫偐傜偺夝摎丅
榋妏宍俙俹俛俻俠俼偺撪晹偵揰俽傪丄俽俻俠俼偑暯峴巐曈宍偵側傞傛偆偵偲傞丅
偡傞偲丄
丂佢俽俻俛
亖120亅佢俽俻俠
亖120亅(180亅(佢俙俠俛亄30亄30)
亖佢俙俠俛
傑偨丄
丂俽俻丗俻俛
亖俼俠丗俻俛
亖俠俙/ 丗俠俛/
丗俠俛/
亖俠俙丗俠俛側偺偱
寢嬊丄仮俽俻俛佷俙俠俛偱偁傞丅
備偊偵丄佢俙俛俠亖佢俽俛俻丂乧乧乧嘆
傑偨丄俽俛亖俙俛/ 亖俛俹丂乧乧乧嘇
亖俛俹丂乧乧乧嘇
堦曽偱丄
丂佢俽俛俹
亖30亄佢俙俛俠亄30亅佢俽俛俻
亖嘆傛傝60
側偺偱丄偙傟偲嘇偐傜仮俽俛俹偼惓嶰妏宍偲傢偐傞丅
傛偭偰丄俹俛亖俹俽丂乧乧乧嘊
偝偰丄
佢俹俽俼
亖360亅佢俹俽俛亅佢俛俽俻亅佢俻俽俼
亖360亅60亅佢俛俙俠亅佢俻俠俼
亖360亅60亅佢俛俙俠亅佢俙俠俛亅30亅30
亖240亅(180亅佢俙俛俠)
亖60亄佢俙俛俠
亖30亄30亄佢俙俛俠
亖佢俹俛俻丂乧乧乧嘋
俛俻亖俽俼偼帺柧丂乧乧乧嘍
廬偭偰嘊,嘋,嘍傛傝
仮俹俛俻佭俹俽俼側偺偱俹俻亖俹俼丂乧乧乧嘐
摨帪偵佢俽俹俼亖佢俻俹俛偵拲堄偟偰偍偔丂乧乧乧嘑
佢俻俹俼
亖佢俽俹俼亄佢俽俹俛亅佢俻俹俛
亖佢俽俹俼亄60亅佢俻俹俛
亖嘑傛傝60丂乧乧乧嘒
嘐,嘒傛傝仮俹俻俼偼惓嶰妏宍偱偁傞丅
亂姶憐亃
側乕傫偐偳偙偐偱尒偨偙偲偁傞傛偆側婥偑偡傞丅
仧搶嫗搒丂Asami丂偝傫偐傜偺夝摎丅
亂偍栺懇偺暋慺暯柺偵傛傞夝摎亃
俙,俛,俠傪暋慺暯柺偱z1,侽,z2偲昞帵偡傞偲
俹偼(侾/俀亄i/俀 )亊z1
)亊z1
俻偼(侾/俀亅i/俀 )亊z2
)亊z2
俼偼(侾/俀亅i/俀 )亊(z1亅z2)亄z2
)亊(z1亅z2)亄z2
偄傑丄
(侾/俀亄i側偺偱丄俹俻亖俹俼偱偁傞丅/俀)亊{(侾/俀亅i/俀
)亊z2亅(侾/俀亄i/俀
)亊z1} 亖(侾/俀亅i/俀
)亊(z1亅z2)亄z2亅(侾/俀亄i/俀
)亊z1
(侾/俀亄i側偺偱丄俻俼亖俻俹傕傢偐傞丅/俀)亊{(侾/俀亅i/俀
)亊(z1亅z2)亄z2亅(侾/俀亅i/俀
)亊z2} 亖(侾/俀亄i/俀
)亊z1亅(侾/俀亅i/俀
)亊z2
備偊偵丄俹俻亖俻俼亖俼俹
仧垽抦導丂廳塱丂戝夘丂偝傫偐傜偺夝摎丅
曈俙俛丆俛俠丆俠俙傪掙曈偲偡傞擇摍曈嶰妏宍偼憡帡偱丄
憡帡斾傪倫丗倯丗倰偲偡傞丅
揰俹傪俙俛偵懳偟偰懳徧堏摦偟丄偦偺揰傪俽偲偡傞偲
仮俙俹俽丆仮俛俹俽偼惓嶰妏宍偱偁傞丅
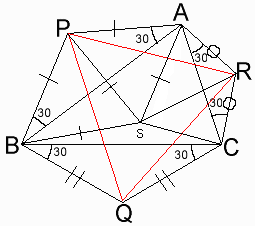
佢俛俙俠亖俁侽亱亄佢俽俙俠亖佢俽俙俼
傑偨丄
俙俛丗俙俠亖俙俽丗俙俼乮亖倫丗倰乯
傛偭偰丄
仮俙俛俠佷仮俙俽俼偱丄佢俙俛俠亖佢俙俽俼
佢俹俛俻
亖佢俙俛俠亄俁侽亱亄俁侽亱
亖佢俙俽俼亄俇侽亱
亖佢俙俽俼亄佢俙俽俹
亖佢俹俽俼乧嘆
俙俛丗俛俠
亖俙俽丗俽俼乮仮俙俛俠佷仮俙俽俼傛傝乯
亖俹俽丗俽俼乮亖倫丗倯乯
傑偨丄
俙俛丗俛俠
亖俛俹丗俛俻
亖俹俽丗俛俻乮亖倫丗倯乯
偙偺俀幃傛傝丄俽俼亖俛俻乧嘇
嘆丆嘇偲俹俛亖俹俽傛傝仮俹俛俻佭仮俹俽俼丅
傛偭偰丄俹俻亖俹俼丅
摨條偵懳徧揰傪偲傞憖嶌傪偟偰丄俻俼亖俹俼丅
亙僐儊儞僩亜
偨傇傫丄Asami偝傫偺夝摎偲傎傏摨偠偩偲巚偄傑偡丅
乮幐楃偱偡偑乯徹柧傪徻偟偔撉傫偱偄側偄偺偱傢偐傝傑偣傫偑丅
杔傕偳偙偐偱尒偨婰壇偑偁傝傑偡丅
亂嶉嬍導丂惸摗丂惤偝傫偐傜偺僐儊儞僩亃
偙偺栤戣偼亀嵟抁僔儏僞僀僫乕栤戣亁偺巹偺夝摎偺拞偵偁傞拞娫壽戣偲帡偨傕偺偱偡丅
俹丄俻丄俼傪拞怱偲偟偦傟偧傟俙俛丄俛俠丄俠俙傪捠傞墌傪昤偗偽摨偠偵側傝傑偡丅
巹偼徹柧傪徣棯偟傑偟偨偑丄崅峑偺嶲峫彂偵傕偙偺俁墌偑侾揰偱岎傢傞徹柧栤戣偑桳偭偨傛偆偵婰壇偟偰偄傑偡丅
偙傟偵偼峏偵娙扨側徹柧偑桳傞傛偆偵巚偊傑偡丅
尒曽傪曄偊傞偲偄傠傫側栤戣偵側傝丄夝摎曽朄傕曄傢傞偺偑偲偰傕偍傕偟傠偄偱偡偹両両
仧嶉嬍導丂惸摗丂惤丂偝傫偐傜偺夝摎丅
俼丄俻傪拞怱偲偟偰偦傟偧傟俙丆俠丂俠丆俛傪捠傞墌俼丄俻傪夋偒丄偦偺岎揰乮俠埲奜偺乯傪俽偲偡傞丅
尫俙俠偺拞怱妏亖佢俙俼俠亖侾俀侽並側偺偱丄拞怱俼懁偺墌廃妏偼俇侽並
傛偭偰
丂佢俙俽俠亖侾俉侽並亅俇侽並亖侾俀侽並
摨條偵偟偰
丂佢俠俽俛亖侾俀侽並
偲側傞偺偱
丂佢俛俽俙亖俁俇侽並亅侾俀侽並亅侾俀侽並亖侾俀侽並
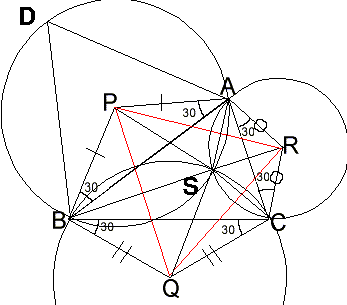
仮俙俛俠偺奜懁偵俙俛傪侾曈偲偡傞惓嶰妏宍俙俛俢傪嶌傝丄偦偺奜愙墌俹傪嶌傞偲
丂佢俙俢俛亄佢俛俽俙亖俇侽並亄侾俀侽並亖侾俉侽並
偲側傞丅
丂傛偭偰丄揰俽偼墌偵撪愙偡傞巐妏宍俙俢俛俽偺捀揰偱摨堦墌忋偺揰偲側傝丄
乽俁墌偼堦揰俽偱岎傢傞乿丅丂傑偨
佢俛俹俙亖侾俀侽並側偺偱丄揰俹偼奜愙墌俹偺拞怱偲側傞丅
丂仮俙俼俽偍傛傃仮俽俹俙偼擇摍曈嶰妏宍側偺偱丄
慄暘俼俹偼尫俙俽偺擇摍暘慄偱偁傞丅
傛偭偰
丂佢俙俼俹亖佢俹俼俽
摨條偵
丂佢俽俼俻亖佢俻俼俠
屘偵
丂佢俹俼俻亖佢俙俼俠乛俀亖俇侽並
丂佢俼俻俹丄佢俻俹俼傕摨偠偱俇侽並偲側傝
丂仮俹俼俻偼惓嶰妏宍丄傛偭偰 俹俻亖俻俼亖俼俹
丂偡偙偟偼娙扨偱偟傚偆偐丅係斣栚偺徹柧朄偱偡丅
仧戝嶃晎丂f-cubed丂偝傫偐傜偺夝摎丅
弶摍婔壗(丠)偱偺夝摎傪峫偊偰傒傑偟偨丅
傑偢柧傜偐偵丄
俙俹亖俛俹丄俻俛亖俻俠丄俠俼亖俙俼偱偁傞丅
傑偨丄
佢俹俙俛亖佢俹俛俙亖佢俠俛俻亖佢俛俠俻亖佢俠俙俼亖佢俙俠俼亖俁侽亱妿偮丄
佢俛俙俠亄佢俙俠俛亄佢俠俛俙亖俀佢俼
偱偁傞偐傜丄
丂佢俹俛俻亄佢俻俠俼亄佢俼俙俹
亖俀佢俼亄俁侽亱亊俇
亖係佢俼
偱偁傞丅 <> 埲忋傛傝丄仮俹俛俻丄仮俻俠俼丄仮俼俙俹傪摍挿偺曈偑廳側傞傛偆偵愙偓崌傢偣傞偲嶰妏宍傪嶌傞偙偲偑偱偒丄偟偐傕偙偺嶰妏宍偺奺曈偼俹俻丄俻俼丄俼俹偱偁傞偐傜仮俹俻俼偵崌摨偱偁傞丅
偙傟偼尵偄姺偊傟偽丄俹俻丄俻俼丄俼俹傪扟慄偲偟偰丄仮俹俛俻丄仮俻俠俼丄仮俼俙俹傪仮俹俻俼偺撪晹傊偲愜傝崬傓偲丄揰俙丄俛丄俠偑堦揰偱廳側傞偙偲偵摍偟偄丅
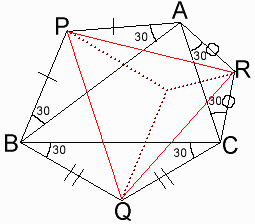
偙偙偱捀妏俹偵拲栚偡傞偲丄
佢俙俹俼亄佢俛俹俻亖佢俻俹俼
亪佢俛俹俙亖佢俙俹俼亄佢俛俹俻亄佢俻俹俼亖俀佢俻俹俼
佢俛俹俙亖侾俀侽亱偱偁傞偐傜丄
亪佢俻俹俼亖俇侽亱
埲壓摨條偵偟偰丄
佢俻俹俼亖佢俹俼俻亖佢俼俻俹亖俇侽亱
備偊偵嶰妏宍俹俻俼偼惓嶰妏宍偱偁傝丄俹俻亖俻俼亖俼俹偱偁傞丅
仧惷壀導丂懞徏丂朏巕丂偝傫偐傜偺僐儊儞僩丅
偙偺栤戣偼丄yoshita孨偺亀僫億儗僆儞偺栤戣亁偲摨偠偱偡偹丅
揰俹丆俻丆俼偼丄嶰妏宍俙俛俠偺奺曈傪堦曈偲偡傞嶰偮偺惓嶰妏宍偺偦傟偧傟偺廳怱偱偡偐傜丅
俠俫俤俠俲偝傫偺栤戣偺夝朄傪傒偰丄夝朄偺懡偝偵傃偭偔傝偟傑偟偨丅