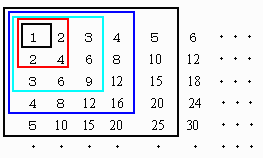
◆静岡県 ヨッシーさんからの解答。
【問題1】
1×1×1の立方体が 3×4×5=60(個)
2×2×2の立方体が 2×3×4=24(個)
3×3×3の立方体が 1×2×3= 6(個)の合計90個・・・答え
【問題2】
まず赤い立方体も含めて考えると、
1×1×1 4×5×6=120(個)
2×2×2 3×4×5= 60(個)
3×3×3 2×3×4= 24(個)
4×4×4 1×2×3= 6(個)の合計210個
このうち、赤い立方体を含むものは
1×1×1 2個
2×2×2 8個
3×3×3 6個
4×4×4 4個 の合計20個
よって、210−20=190(個)・・・・答え
【問題3】
・1×1×1
a×b×c=abc
・2×2×2
(a-1)(b-1)(c-1)=abc-(bc+ca+ab)+(a+b+c)-1
・3×3×3
(a-2)(b-2)(c-2)=abc-2(bc+ca+ab)+22(a+b+c)-23
・・・・・・・・・・・
・c×c×c
(a-c+1)(b-c+1)(c-c+1) =abc-(c-1)(bc+ca+ab)+(c-1)2(a+b+c)−(c-1)3立方体の個数は
| c×abc-{1+2+・・・+(c-1)}(bc+ca+ab)+{12+22+・・・+(c-1)2}(a+b+c)−{13+23+・・・(c-1)3} |
| =abc2− | c(c-1)(bc+ca+ab) 2 | + | c(c-1)(2c-1)(a+b+c) 6 | - | {c(c-1)}2 4 |
| = | c(c+1){(c-1)(c-2a-2b)+6ab} 12 | ・・・答え |
【コメント】
問題3もこれで完全解です。
a=b=cのときは、
| 13+23+・・・c3= | {c(c+1)}2 4 | ですね。 |
◆岐阜県 水の流れさんからの解答。
掲示板の Knelさんの質問の参考にと思いまして。
| 問題 13+23+33+・・・+n3
を等差数列を正方形に配置して、証明します。 |
<導き方>

このように等差数列を正方形に配置して、各正方形内の数の和をS(n)とおく。
例えば、S(1)=1 ,S(2)=1+2+2+4=9
S(3)=1+2+3+2+4+6+3+6+9=36,
・・・,
S(n)=?
次に、2つの連続する正方形の作る逆L字形の部分の数の和をT(n)とおく。
例えば、T(1)=1、T(2)=2+4+2=8 ,
T(3)=3+6+9+6+3=27,・・・,
T(n)=?(ただし、T(1)=1は特別扱いにする)
そこで、n番目の正方形を考えてみると、第1行の数の和R(1)は
| R(1)=1+2+3+・・・+n= | n(n+1) 2 |
そして、第i行の数の和R(i)は R(i)=iR(1)
したがって、n番目の正方形内の数の和S(n)は
S(n)
| =R(1)+R(2)+R(3)+・・・+R(n) |
| =(1+2+3+・・・+n)× | n(n+1) 2 |
| ={ | n(n+1) 2 | } | 2 |
また、n番目の逆L字形の部分の数の和をT(n)は
T(n)
| =S(n)−S(n−1) |
| ={ | n(n+1) 2 | } | 2 | −{ | n(n−1) 2 | } | 2 |
| = | 1 4 | {(n+1)2 −(n−1)2} |
| =n3 |
ところで、T(1)+T(2)+T(3)+・・・+T(n)=S(n)
ゆえに、
13+23+33+・・+n3
| ={ | n(n+1) 2 | } | 2 |
すなわち、はじめのn個の立方数の和は第1行の数の和の平方に等しい。
◆岐阜県 水の流れさんからの解答。
ATOM さんの平方数の和(掲示板)を別方法で求めてみました。
| 問題 <平方数の和S(n)を求める方法> 12+22+32+・・・+n2
を 自然数を正方形に配置して、証明します。 |
<導き方>
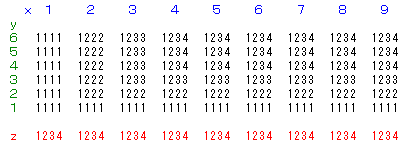
このように自然数を正方形に配置する。
k番目の逆L字形の部分の数の和L(k)は
L(k)
| =1+2+3+・・・+(k−1)+k×k |
| = | k(k−1) 2 |
+k2 |
| = | 3 2 |
k2− | 1 2 |
k |
次に、n番目の正方形内の数の和U(n)は、
U(n)
| =L(1)+L(2)+L(3)+・・・+ L(n) |
| = | 3 2 |
(12+22+・・・+n2)− | 1 2 |
(1+2+・・・+n) |
| = | 3 2 |
S(n)− | 1 2 | n(n+1) 2 |
・・・(1) |
一方、n番目の正方形内の各行の数の和は一定で、
| 1+2+3+・・・+n= | n(n+1) 2 |
| したがって、U(n)=n・ | n(n+1) 2 |
・・・(2) |
よって、(1)と(2)より ,
| 3 2 |
S(n)− | 1 2 | n(n+1) 2 |
=n・ | n(n+1) 2 |
・・・(2) |
S(n)
| = | 2 3 |
n(n+1) 2 |
{n+ | 1 2 |
} |
| = | n(n+1)(2n+1) 6 |
すなわち、自然数の平方数の和は
| n(n+1)(2n+1) 6 | となる。 |
◆山梨県 Footmark さんからの解答。
【問題3】
与えられた直方体の任意の頂点を原点にし、3辺a,b,cがそれぞれx値,y値,z値となるようにxyz座標をとります。
そこで、立方体の8頂点の内で原点からの距離が最長である頂点が、直方体に含まれる各格子点である場合を考えます。
明らかにx=0やy=0やz=0の格子点には立方体は存在しません。
よって、立方体が存在する格子点は、
座標(x,y,z)が1≦x≦a,1≦y≦b,1≦z≦cのa*b*c個です。
a*b*c個の各格子点において、存在する立方体の数は以下となります。(注)
(ただし、例は9×6×4の直方体ですが、以後も同様にします。)
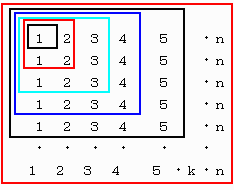
当然のことですが、各格子点における立方体の数は、x値,y値,z値の内の最小値です。
条件より、cはa,b,cの内で最小です。
そこで、1≦x≦cのc個と、
c<x≦aの(a-c)個に左右に分割します。
上の例で左側にある1≦x≦cをL、
上の例で右側にあるc<x≦aをRとします。
そこで、Lを以下のように1≦y≦cのc個と、
c<y≦bの(b-c)個にさらに下上に分割します。
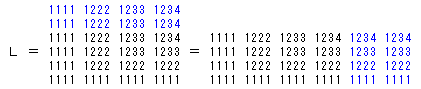
Lの最右辺は、
(12の1倍)+(22の2倍)+・・+(c2のc倍)と
12+22+・・+c2の(b-c)倍の和です。(注)
明らかに、
(12の1倍)+(22の2倍)+・・+(c2のc倍)は
13+23+・・+c3 です。
| ∴ L={ | c(c+1) 2 | } | 2 | +(b-c) | c(c+1)(2c+1) 6 |
同様に、Rも以下のように1≦y≦cのc個と、
c<y≦bの(b-c)個にさらに下上に分割します。
Rの最右辺は、12+22+・・+c2の(a-c)倍と
1+2+・・+cの(a-c)(b-c)倍の和です。(注)
| ∴ R=(a-c) | c(c+1)(2c+1) 6 | +(a-c)(b-c) | c(c+1) 2 |
よって、
求める立方体の数
| =L+R |
| ={ | c(c+1) 2 | } | 2 | +(a+b-2c) | c(c+1)(2c+1) 6 | +(a-c)(b-c) | c(c+1) 2 |
| = | c(c+1) | (c-1)(c-2a-2b)+6ab 12 |
| 【答え】 | c(c+1){(c-1)(c-2a-2b)+6ab} 12 |
個 |
(注) 詳細は『正方形は何個?』で示したので省略しました。
[ P・S ]
直方体の3辺の最小値をtとし、他の2辺との差をそれぞれd1,d2とすると、以下のような綺麗な式になります。
求める立方体の数
=(1〜tの3乗和)+(d1+d2)(1〜tの2乗和)+(d1*d2)(1〜tの1乗和)
当然ですが、
| a=b=cのときは3乗和{ | c(c+1) 2 | } | 2 | となります。 |
また、3辺とも1なら1、2辺だけ1なら残りの1辺、1辺だけ1なら残り2辺の積となります。
いずれの場合も辺長1以外の立方体は不可能なので、これも当然です。
ところで、この解法や結果から判るように、a,b,cの内で最小なものさえ判明すれば解は得られます。
ですから、最小な辺でない他の2辺の大小関係は、解を得るのに必要ありません。