∠GBC=∠GCA=30度です。
即ちG=Dです。
よって AB=AD
【問題2】
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
∠ABC=2×∠ACBであるので
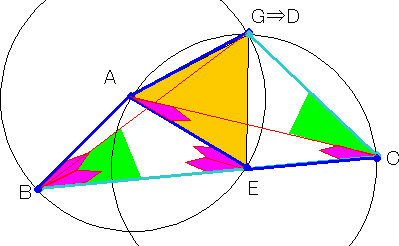
AB=AE=ECである点EをBC上にとることが可能です。
Aを中心としBEを通る円と Eを中心としACを通る円との交点Gを下図のようにとります。
すると三角形AEGは正三角形なので頂角は60度であり、円周角と中心角の関係から
∠GBC=∠GCA=30度です。
即ちG=Dです。
よって AB=AD

【問題2】
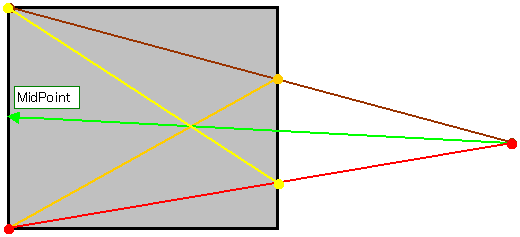
『1/8の正方形』と基本的には同じです。
◆出題者のコメント
問題1、問題2ともにすばらしい解答で感激いたしました。
特に問題2の方は、私が長年かけて思いついた解答とは全く違うエレガントなもので、出題して本当によかったと思います。
◆新潟県 加藤 英晴 さんからの解答
【問題1】
AB=AEとなるような点Eを線分BC上にとる。
∠ACE=x,線分AB=aとおくと,
仮定より,∠BDC=120°−x,
BC=2acos2x+a.
△DBCで正弦定理を用いて,
| DC= | a(4(cosx)2−1) √3cosx+sinx |
. |
◆出題者のコメント
新潟県 加藤英晴さんの答えに対するコメント
<問題1について>
計算の過程は省略されていますが、正解です。
幾何の方法にもチャレンジして下さい。