―――

◆神奈川県 @JJJJJJ さんからの解答。
【問題1】
平面を赤色と青色の2色で塗り分けるとします。
距離1離れた点は全て異なる色である(仮定1)とすると、赤色のある点Oを中心とする半径1の円周上の点は全て青色になり、これは仮定1に反します。
【問題2】
平面を赤色、青色、黄色で塗り分けます。
ある点Oを赤色とし、点Oを中心として半径1の円を描き
円周上の点を半時計回りにABCDEFとします。
ここでA(青色)、B(黄色)、C(青色)、D(黄色)、E(青色)、F(黄色)は一辺が1の正六角形を構成し、
AB=BC=CD=DE=EF=FAです。
次に点B(黄色)を中心として半径1の円弧AOCを描くと
円弧AOC上の点は全て、赤色か青色です(*1)。
次に点D(黄色)を中心として半径1の円弧COEを描くと
円弧COE上の点は全て、赤色か青色です(*2)。
次に点F(黄色)を中心として半径1の円弧EOAを描くと
円弧EOA上の点は全て、赤色か青色です(*3)。
今、円弧AOC上の点で点Oから点A方向に向かって直線距離が
|
1 ―――  | の距離にある点をA’とします。 |
また、円弧COE上の点で点Oから点C方向に向かって直線距離が
|
1 ―――  | の距離にある点をC’とします。 |
また、円弧EOA上の点で点Oから点E方向に向かって直線距離が
|
1 ―――  | の距離にある点をE’とします。 |
すると三角形A’C’E’は一辺の長さが1の正三角形になります。
ところが、(*1)(*2)(*3)より、3点A’C’E’はすべて赤色か青色かでなければならないので、距離が1離れた、同じ色で塗られた点があることになります。
◆神奈川県 いわし さんからの解答。
【問題2】
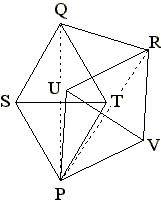
△PQRをPQ=PR= , QR=1の二等辺三角形とし、
, QR=1の二等辺三角形とし、
△PST, △QST, △PUV, △RUV が一辺の長さが1の正三角形となるように点 S, T, U, V を定めます。
(「7人のコビト」の配置)
三色を赤、青、黄とします。
題意を否定した命題を仮定し、それを(*)とします。
一般性を失うことなく、Pを赤とします。
すると(*)より、SとT, UとVはいずれも一方が青、他方が黄ですから、Q, Rはともに赤となりますが、これは(*)に矛盾します。
よって背理法により題意は示されました。 (終)
【問題3】
「題意の点の組が無限個存在する」…(#) ことを証明します。
2色を赤、青とします。
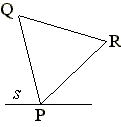
平面上に長さ1の線分sをとります。
s上には、少なくとも一方の色の点が無限個存在します。
それを赤とし、s上の赤い点の集合をs'とします。
P∈s'とし、一辺の長さが1の正三角形PQRをつくります。
△PQRをsに平行に動かしたとき、
QまたはRが赤となるP∈s'が無限個存在すれば、
このPとQまたはRによって(#)は成立しています。
また、QまたはRが赤となるPが有限個ならば、無限個のPに対してQ, Rはともに青ですから、
このQ, Rによって(#)は成立しています。
よって(#)が証明されました。(終)
◆出題者の安里歩安彼 さんからのコメント。
いわしさん、解答ありがとうございました。
特に問題3は僕が考えたものと違っていたので、とても新鮮に感じました。
参考までに、僕の考えた解答をあげておきます。
点pを中心として、半径1の円を描きます。
この円の円周をPとします。
点pの色を赤として、
1.Pに赤の点が無限にある場合
当然、題意を満たす点の組は無限にある。
2.Pに赤の点が有限にある場合
Pに、青の点が無限にあることになり、赤の点は有限なので距離が1離れたP上の点の組は無限にある。
以上より、命題は示されました。
追加問題:
4色の場合は、どうでしょうか?
◆東京都 建築家 さんからの解答。
平面が4色で塗りきれたとします。
そうすると必ず3色が隣に存在するような点Pが存在します。
|P-P'|<δとなる点はその3色で塗り分けられているとする。
そのとき|P-Q|=1となる点があって、
|Q-Q’|<δとなる点Q’は必ずどの3色にもなり得ない点が存在するような点Qが存在します。
(→これから問題1,2がいえます)
この時に|Q-R|=1となる点の中にははじめの3色にも、点Qの色にもなりえない点が存在します。
よって平面は4色で塗り分けられません。
n次元に対して同様のことが((n-1)色)いえますでしょうか?