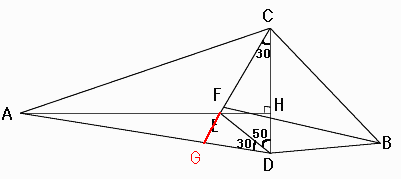
◆Takaaki Yosiduさんからの解答。

【コメント】
この図をよく見て考えてみてください。
∠CDBの大きさがわかった方、またメールくださいね。
◆海外の高校生 Masanao Chidaさんからの解答。
答えは80度
◆海外 nymc さんからの解答。
この問題の図において、点A, C, D, E, H の位置関係は
『中学生からの挑戦状Part6』のそれぞれ点C, D, B, A, H の位置関係と同じである。
すなわちPart6の(C, D, B, A, H)をそれぞれ(A, C, D, E, H)と置きかえると
この『中学生からの挑戦状Part8』の左半分と同じ図形になる。
Part6の答えを利用すると、この問題では
∠ACE=40度となる。
すると、
∠CAD=180−(∠ACD+∠ADC)
=180−(70+80)
=30度
よって、
∠CBF=∠CAD=30度
ここで、BFとCDの交点をGとすると、平行線の錯角なので
∠BGD=∠ADG=80度
よって、
∠BCG=∠BGD−∠CBG
=80−30
=50度
三角形BCDはBD=CDの二等辺三角形なので
∠CDB=180−2x∠BCG=80度(答え)
左半分がPART6と同じだということに気づけばあとは簡単。
どうやっても解けますね。
◆東京都 榎本 孝一 さんからの解答。
掲載されている解答と違う答がでました。
∠CBDが30°になるところまでは,既出の問題・解答と同じなので省略します。
FD//CBなので,∠BFDも30°となります。
ここで,△CFDを辺CDについて折り返し,△CODを作る。
このとき,△CFOは正三角形となり,
OC=OFであり,∠CBF=30°,∠COF=60°であること等から,
点Oは△BCFの外心となります。
よって,OC=OF=OBです。
また,題意より,DC=DBであることから,
△DOC≡△DOBとなります。
よって,∠ODC=∠ODBで,
先ほどの,折り返した関係から,
∠CDF=∠CDOで,FD//CBより,
∠BCD=∠CDFとなります。
これらのことから,∠BCD=x とすると,
∠CBD= ∠BCD=∠CDF=∠CDO=∠BDO=x
となり,△BCDの内角について考えると,
∠BCD+∠CBD+∠CDB
=∠BCD+∠CBD+∠CDO+∠BDO
= x + x + x + x
=4x
=180
よって,x=45°なので,
∠CDB=90°・・・(答)
◆大分県 ケンタロウ さんからの解答。
まず、線分BDをB側に延長線を引き延長線上の任意の点Gをおく。
∠CDBをXとすると、問題から△CBDは二等辺三角形であることがわかる。
そのことから
| ∠CBD=90− | X 2 |
(△CDBより) |
よって、∠CBD+∠CBF=180度から
| 90− | X 2 |
+50+X=180 |
故に、∠CDBは80度。
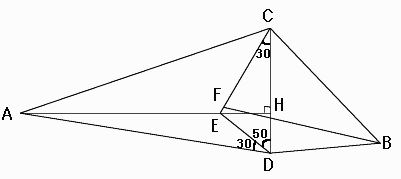
◆静岡県の中学校3年生 Mr.X さんからの解答。
CB//EDだから、∠CDE=∠DCB=50°(錯角)
辺CD=辺DBで、二等辺三角形になるから、
∠DCB=∠DBC=50°
50°+50°=100°
180°−100°=80°だから∠CDB=80°
◆静岡県 村松 芳子 さんからの解答。
まず、∠CAD=30°を求める。
(挑戦状のpart6を参考にして求める)
したがって、∠CBF=30°
次に、図のように、線分FBを一辺とする正三角形FBGを作図する。
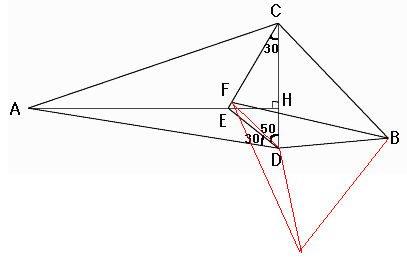
∠BFD=∠DFG=30°、FB=FG、FDは共通より、
△FDB≡△FDG
ゆえに、DB=DG
条件よりCD=DBだから、DB=DG=CD
したがって、C,B,GはDを中心とする同一円周上の点である。
∠CBG=30°+60°=90°だから、∠CDG=180°
すなわち、CDGは直線である。
また、∠FBG=60°、∠FCG=30°より、C,F,Gは点Bを中心とする同一円周上にあると言える。
ゆえに、BC=BF=BG(半径)
ゆえに、△BCFは頂角30°の二等辺三角形である。
ゆえに、∠BCF=75°
ゆえに、∠BCD=75°−30°=45°
ゆえに、△CDBは底角45°の二等辺三角形である。
したがって、∠CDB=90°
(終わり)
「寄せられた解答」のなかで、榎本さん以外は皆80°となっていますが、これは間違いです。
この間違いについて説明します。
∠CDB=80°なら、∠DCB=∠DBC=50°
∠CDE=50°だから、CB//ED
条件よりFD//DBだから、点Fと点Eは一致することになる。
図のような、角度の関係となる。一見、正しい関係のように見えます。ところが....
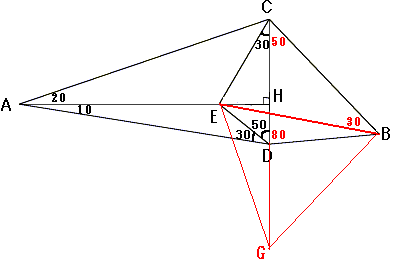
CDをDの方向に延長し、BD=DGとなるように、Gをとる。
∠BDG=100°だから、∠DBG=∠DGB=40°
∠EDB=130°、∠BDG=100°だから、
∠EDG=130°
ゆえに、△EDB≡△EDG(二辺夾角より)
したがって、△EGBは正三角形である。
∠ECG=30°(円周角)、∠EBG=60°(中心角)の関係より、C,E,GはBを中心とする同一円周上の点である。
ゆえに CB=EB=GBとなり、∠BCE=∠BEC=75°
ところが、図では∠BCE=80°であるから、図の角度が間違っていることになる。
すなわち、FとEは異なる点でなければならない。