『５つのナップザック』解答

◆愛知県　Y.M.Ojisan さんからの解答。

【問題１解答】　１２９６通り

【考え方】

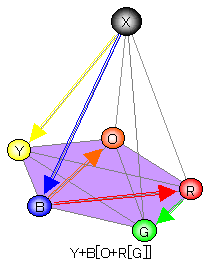
常に全体が入っている大きなナップザックＸを考え、パッキング関係を矢印で表すとき、
たとえばＹ＋Ｂ[Ｏ+Ｒ[Ｇ]]は図１のように表せる。

図１

図２に示すように「矢印」は１つのナップザック（例：Ｒ）につき全て５種ある。

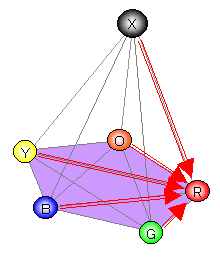図２

従って，その組み合わせは５^５＝３１２５ある。
このうち下図に示すように、ループを含む関係は存在しえず、この分を差し引くことにより、全組み合わせ数を計算できる。

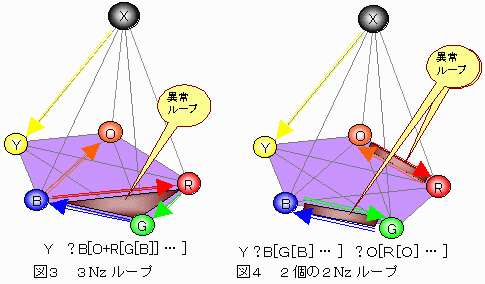
【記号】

Ｎｚ　：ナップザック

_NＬ_M
＝：Ｎ個からＭ個のＮｚを取り出しループを作る場合の数
＝_NＣ_M×_Ｍ-1Ｐ_Ｍ-1

ＮＢ_M
＝：図２における「Ｘ」相当が複数 (1+N-M)個、ＮｚがM個ある場合のループができる場合の数を意味するとする。

下図参照

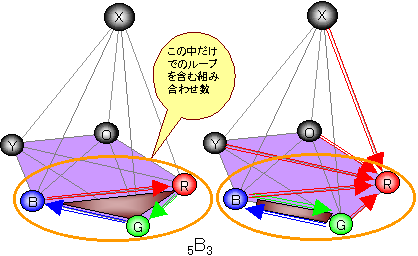
_NＢ₂＝１

_NＢ₃＝₃Ｌ₃＋Ｎ×₃Ｌ₂

NＢ4＝4Ｌ4＋Ｎ×4Ｌ3＋4Ｌ2×4-2Ｌ2／２＋（Ｎ2−NＢ2）×4Ｌ2

であり、
答え＝Ｎ^Ｎ−_NＢ_Nである。

【計算】

以下、ループの大きさと数で分類し、計算する｡

○５Ｎｚのループの数
　₅Ｌ₅＝１×₄Ｐ₄＝２４

○４Ｎｚのループの数
　₅Ｌ₄×５^5-4
＝₅Ｃ₄×₃Ｐ₃×５
＝１５０

○３Ｎｚ＋２Ｎｚのループの数
　₅Ｌ₃×_5-3Ｌ₂
＝（₅Ｃ₃×₂Ｐ₂）×１
＝２０

○３Ｎｚのみのループの数
　₅Ｌ₃×（５^5-3−₅Ｂ₂）
＝₅Ｃ₃×₂Ｐ₂×(５²−１)
＝４８０

○２組の２Ｎｚのループの数
　₅Ｌ₂×_5-2Ｌ₂／２×５^5-2-2
＝（₅Ｃ₂×１×_5-2Ｃ₂×１）／２×５
＝７５

○１組の２Ｎｚのループの数
　₅Ｌ₂×（５^5-2−₅Ｂ₃）
＝₅Ｌ₂×（５³―₃Ｌ₃−５×₃Ｌ₂）
＝₅Ｃ₂×１×（１２５―１×₂Ｐ₂−５×₃Ｌ₂）
＝１０８０

以上より
　₅Ｂ₅
＝２４＋１５０＋（２０＋４８０）＋７５＋１０８０
＝１８２９

よって　
答え＝３１２５−１８２９＝１２９６

【蛇足】

Ｎ＝２
　２²−₂Ｂ₂＝３

Ｎ＝３
　３^３−₃Ｂ₃
＝２７−２−９
＝１６

Ｎ＝４
　４^４−₄Ｂ₄
＝２５６−６−３２−３−９０
＝１２５

Ｎ＝６

６６−○６Ｎｚループ−○５Ｎｚループ−○４Ｎｚのみループ
−○４Ｎｚと２Ｎｚループ−○３Ｎｚのみループ−○３Ｎｚ２個ループ
−○３Ｎｚと２Ｎｚループ−○２Ｎｚのみループ−○２Ｎｚ２個ループ
−○２Ｎｚ３個ループ

【出題者のコメント】

思い付かないユニークな解法には脱帽しました。
実は、この問題の創作時に偶然発見したのですが、Ｎ個の時の一般解も存在します。
問題２として出題します。

◆愛知県　Y.M.Ojisan さんからの解答。

【問題２】　（Ｎ＋１）^N-1通り

【証明】

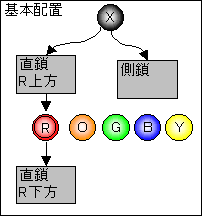
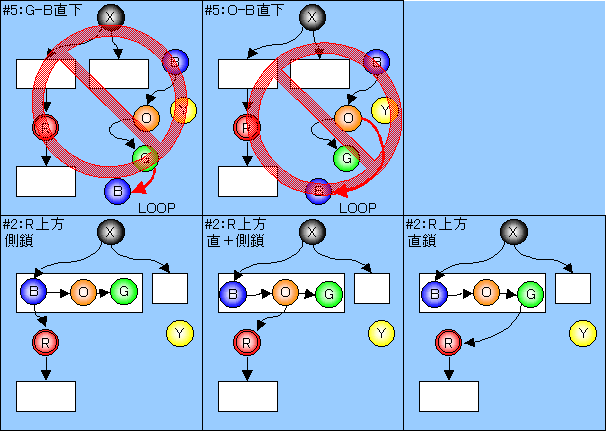
下図のように最初の１Ｎｚ（Ｒ）だけ特別扱いする。
すると、その他Ｎ−１個の入る位置は、

（１）Ｒの上方Ｘとの間に繋がる場合（尊属、いとこ）
（２）Ｒの下方（子孫）
（３）側鎖（はとこ）

の何れかである。

次に２番目（Ｏ）の位置をどのＮｚに入るかで分類すると、
下図のように（Ｎ＋１）ケースある。

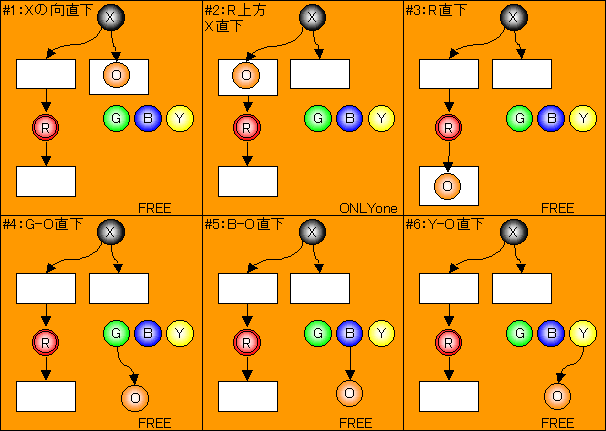
すなわち、自分以外の各Ｎｚに入る（以後直下）(Ｎ−１)ケースと「Ｘ」の直下で、「Ｒの上方」の場合と「Ｒの直系でない：側鎖」の場合の２ケースの合計である。
　これは１番目（Ｒ）以外のその他のＮｚに関しても対称性から全く同じである。

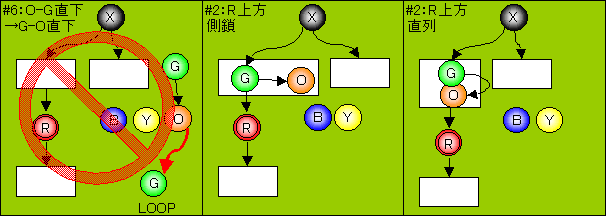
次に３番目（Ｇ）の結合を考えると、
全部で（Ｎ＋１）×（Ｎ＋１）タイプがあるが、このうち下図の禁止マークの２タイプは存在しえない。
しかし、「Ｒ上方」への結合タイプで、各１タイプにつき直列になる場合と側鎖になる場合の２ケースが存在するため、２番目（Ｏ）の１ケースにつきそれぞれ（Ｎ＋１）ケースが存在する。
　すなわち、(Ｎ＋１)²　ケース存在している。

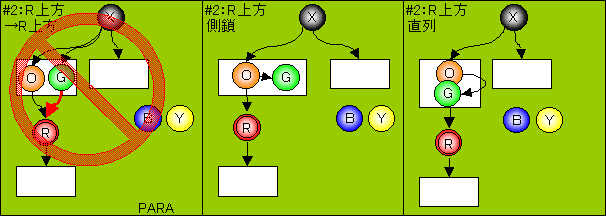
さらに、Ｎｚ（Ｂ）（Ｙ）。。。。を追加していっても、
下２図のようにループがあれば、
その数だけ、必ず「Ｒ上方」への結合部において、
直列、並列の側鎖ケースの数がその数分増え、
「Ｒ上方」部に既に先客がある場合はその先客の直下において、
さらにその分側鎖ケースが＋１されるので、
必ず１タイプにつき（Ｎ＋１）ケースが存在する。

よって、Ｒを除く（Ｎ−１）個のＮｚのケースの積であり、
全部で　(Ｎ＋１)^N-1とおりある。

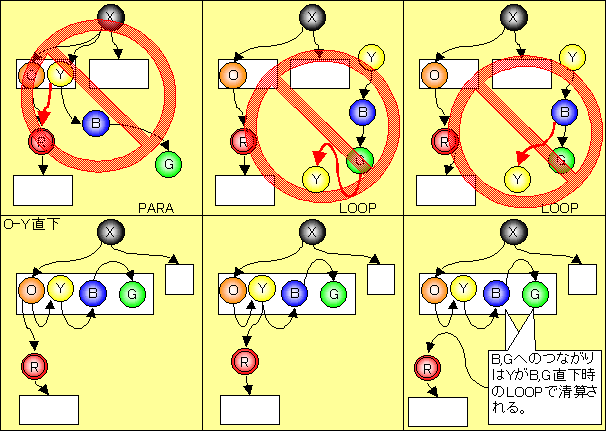
【感想】

脱帽はこちらです。
問題１で　正攻法では場合分けが多くなるので、裏側から攻撃し、一応の成果はあったのですが、一般解へは到達しませんでした。

Ｎ＝１，２，３の場合の数１、３、１６をしらみ潰しで確認し、
Ｎ＝４を飛ばして　Ｎ＝５の１２９６を正攻法の答えで確認し、解答を書き終えて蛇足をつける段階でのことです。

Ｎ＝４の場合の答えを計算したら
　１２５＝５³。

まさかの気持ちで６⁴を計算したら１２９６。

さらに、Ｎ＝６，７でも成立。
この奇策は無駄であったことが分かり、かなり愕然としました。
一般解は正攻法の末にあるらしいのですから。

結局しりきれとんぼの蛇足とともに、ほぼ間違いなく「問題２」が出るであろうことを予測しつつ、【問題１】の解答を提出しましたが。

しかし、どうしてこんなに綺麗な解なのでしょう。
綺麗に解きたくて、その単純な構造を見つけようとこの１週間悩みに悩んだのですが、結局それは出来ませんでした。

【出題者のコメント】

【問題１】,【問題２】とも全て正解です！
ただ、出来る事なら一般解の証明は一般のＮ個から直接に証明して頂きたかったですけど・・。

出題者の山梨県　Footmark さんの証明

【問題１】

　 (５＋１)^5-1
＝ ６⁴
＝ １２９６

【答え】１２９６ 通り

【問題２】

【答え】　(Ｎ＋１)^N-1 通り

【証明】

ナップザックの持ち主にも登場してもらい、各ナップザックは人格化して目と口と耳を持つものとします。

現実に１つの収納の仕方があるとして、次のことを行うものとします。

まず、ナップザックの持ち主から、自分に直接見えるナップザックがあれば、ＲＧＢ値順に告げてから、最後に「ありません」と報告します。

次に、色を告げられたナップザック順に、自分の中に直接見えるナップザックがあれば、ＲＧＢ値順に告げてから、最後に「ありません」と報告します。
これを、自分の色を告げられているのに報告が済んでないナップザックがある間は、告げられた順に繰り返します。

この操作によって、収納の仕方が同じなのに全報告が２通り以上になったり、逆に２通り以上の収納の仕方なのに全報告が同一になったりせず、
[収納の仕方]と[全報告のあり方]が１対１対応になります。
それ故、[収納の仕方]を数えるのは、この[全報告のあり方]を数えるのと同じです。

現実にあり得る全報告ならば、すべての「ナップザック」が誰かに１回だけ告げられる筈です。
しかも、１つのナップザック(または持ち主)からの報告では、告げられる「ナップザック」は常にＲＧＢ値順が保たれています。
また、「ありません」と発音する数は、ナップザックの持ち主の分も含めて
(Ｎ＋１)個ですが、最後に報告するナップザックは常に「ありません」だけしか報告しない筈ですから、これを除くとＮ個になります。

ですから、この問題は、Ｎ個の「色の違うナップザック」とＮ個の「ありません」との計２Ｎ個を、現実にあり得る全報告として１列にさせる並び方の問題になります。

〔収納の仕方〕	〔全報告のあり方〕
１＋２＋３＋４＋５	１２３４５＊＊＊＊＊
２<３>＋１＋４＋５	１２４５＊＊３＊＊＊
３<４>＋５<１>＋２	２３５＊＊４＊１＊＊
４<５<１>>＋２＋３	２３４＊＊＊５＊１＊
５<１＋２>＋３＋４	３４５＊＊＊１２＊＊
１<２<３>>＋４<５>	１４＊２＊５＊３＊＊
２<３＋４>＋５<１>	２５＊３４＊１＊＊＊
３<４<５>>＋１<２>	１３＊２＊４＊＊５＊
４<５<１＋２＋３>>	４＊５＊１２３＊＊＊
５<１<２<３<４>>>>	５＊１＊２＊３＊４＊

Ｐ<Ｑ>は、ナップザックＰにＱ状態が収納されている状態です。
また、数字はナップザック名、＊は「ありません」を表します。
数字の若い順がナップザックのＲＧＢ値順になるものとします。

ここで、見方を変えて考えてみます。
まず先に、Ｎ個の「ありません」を１列に並べて置きます。
あとから、Ｎ個のナップザックを列に入れていくものとします。
「ありません」が何処にあっても構わないものとして、ＲＧＢ値順に「ナップザック」の入れる位置を選んでいきます。

選べる位置は、Ｎ個の「ありません」の直前の、
位置[１]〜位置[Ｎ] か、
最後の位置[Ｎ+１]がある筈です。
最初の「ナップザック」の入る位置は当然(Ｎ＋１)通りあります。

２番目以降の「ナップザック」も、入ろうとする位置[ｋ]
(ｋは１≦ｋ≦Ｎ＋１の整数)に、既に先客の「ナップザック」が幾つあろうが、
同一の位置[ｋ]内では常に最後になるので、やはり(Ｎ＋１)通りあります。

それ故、「ありません」が何処にあっても構わないものとすると、全報告のあり方は
(Ｎ＋１)^N 通りです。

また、各「ナップザック」が列に入るには、任意の１個の位置[ｋ]
(ｋは１≦ｋ≦Ｎ＋１の整数)を選んでいるので、重複して報告されることは起き得ません。

そこで、「ありません」が現実にある得る位置を考えてみます。
何故なら、列の中の「ありません」の位置によっては、全報告が途中で途切れてしまい、全報告から漏れる「ナップザック」もでるため、現実にあり得る全報告とはならないからです。

すべての「ナップザック」が漏れなく告げられるためには、全報告が最後まで途切れない必要があります。

もし、全報告の先頭から数えて、「ありません」と発音した数が「ナップザック」を告げた数を上まわってしまえば、その時点で、自分の色は告げられているのに報告が済んでない「ナップザック」はなくなり、全報告は途切れてしまいます。

元々、「ナップザック」と「ありません」は同数ずつあったのですから、「ありません」が上まわった状態では、必ず全報告から漏れた「ナップザック」がある筈です。

それ故、Ｎ個の「ナップザック」とＮ個の「ありません」とが一緒になって１列になる並び方の内で、先頭から連続して任意の個数を選んでも、常に「ナップザック」の数が「ありません」の数より少なくならない、並び方をする必要があります。

これは、「ナップザック」の色を区別しなければ、Ｎ個ずつの「ナップザック」と「ありません」との『金太郎飴整列』に他なりません。

適当な表現がないため出題者が勝手に命名したものですが、[ 同数の２種類が一緒になって１列に並んでいる状態において、先頭から連続していかなる個数を選んでも、常に特定した種類の個数が別の種類の個数より少なくならない並び方 ]を、以下は「金太郎飴整列」と表現します。

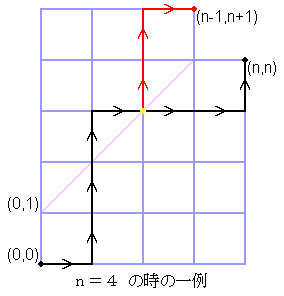
この『金太郎飴整列』の仕方の数は、ｘｙ平面で考えると、
「ナップザック」を［(+1,0)の移動］に、
「ありません」を［(0,+1)の移動］にすることによって、
点(０,０)から点(Ｎ,Ｎ)までの、Ｙ＝Ｘ＋１ 上の点と接しない最短経路の数の問題に置き換えられます。

点(０,０)から点(Ｎ,Ｎ)までの、すべての最短経路の数は
_2NＣ_N

一方、Ｙ＝Ｘ＋１ 上の点に接する最短経路の数は、
最後に Ｙ＝Ｘ＋１ 上の点に接してからの移動を、Ｘ方向とＹ方向とを入れ替えてやれば、
点(０,０)から点(Ｎ-１,Ｎ+１)までの最短経路の数と１対１対応になるので
_2NＣ_N-1

それ故、求める金太郎飴整列の仕方の数は

2NＣN−2NＣN-1＝

2NＣN Ｎ＋１

一般に、『金太郎飴整列』を、条件に含めた場合の数は、条件に含めない場合の数の

１ Ｎ＋1

になります。

ところで、『金太郎飴整列』の条件がなければ、
(Ｎ＋１)^N なので

(Ｎ＋１)N Ｎ＋１

＝(Ｎ＋１)N-1

いずれのナップザックも、重複して報告されることもなく、全報告からも漏れることもなければ、すべての「全報告のあり方」に対して、必要にして十分に条件を満たしています。

「収納の仕方」に置き直して表現すれば、次のようになります。

いずれのナップザックも、重複して収納されることもなく、ナップザックの持ち主に直接であれ間接であれ所持されるのであれば、すべての「収納の仕方」に対して、必要にして十分に条件を満たしています。

よって、Ｎ個のナップザックを収納させる仕方は
(Ｎ＋１)^N-1 通り、あります。

証明は終わりです。

[補足]

2nＣn ｎ＋1

は、カタラン数(列)とも言われ有名です。

【余談】

パソコン上でＮ個のフォルダをこれらとは別の１個の特定のフォルダに収納する方法と考えると、この問題もにわかに現実性を帯びてきます。
創作当初は『フォルダの収納』問題でしたが、フォルダはウインドウズでの呼び方だし、ウインドウズもパソコンも知らない方にも良いように『５つのナップザック』問題に改題して出題しました。

◆愛知県　Y.M.Ojisan さんからの解答。

【まえがき】

（１）　出題者のコメント（Ｎから．．．）について

御指摘のとおりです。
ただ、現在の私の興味は問題を解くこと自身から、可能な限り絵と単語程度を用い、言語・記号式を介さず視覚的に証明の内容を伝えられないかに移っています。
この際、一般化したものを絵にするのは難しいところがあり、一般化が容易に推定可能であれば、むしろ特定して描画した方が理解が早いのではと考えています。

（２）　金太郎飴整列問題

　「出題者模範解答」も冒頭の「５角錐の方法」もカタラン数の
１／（ｎ＋１）の意味が分かっていない私にとっては　単純構造で多めに数え、条件を満足しないもの
｛報告の途切れ　、ループのもの　｝を差し引く点では同じです。
独立なＮ−１次元の事象として解釈をつけたいという欲求とは、大幅な程度の差はあれ、異なります。

　以下は数学的には「出題者模範解答」の焼き直しでありカンニングではありますが、自分の中で腑に落ちた解答です。

【洞窟探検の補題】

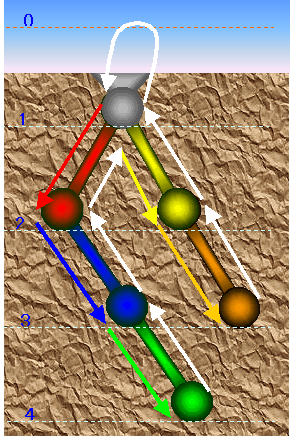　【図１】

図１のように、Ｎ色の洞窟がループを作らずに端で繋がっていて、入り口が一つの２次元面上の洞窟の探検を考えます。
これは一つの迷路問題であり，ループが無いので右手の法則（右手を右側の壁から離さないで探検する）を用いれば、全ての洞窟を１往復して外に出ることが出来ます。

この時探検家は洞窟の構造の地図を後で作成するために、次のように記録します。

（１）入り口広間（黒）から始め、初めて通る洞窟の場合はその色（Ｒ，Ｇ，Ｂ．．）を記録

（２）一度通過した洞窟は「済」の記号：Ｗを記録

（３）最後に外に出て探検「済」としてＷを記録

ここでやめておけば良かったのですが探検家は確認のために何べんも探検し、記録を続けて記入して行きました。
記録は全て正しかったのですが、紙が汚れてどこが最初でどこが最後のＷか分からなくなりました。
周期が２Ｎ＋１であることは分かります。
図２参照。

　【図２】

ところが、実はこの記録からどこが入り口かは分かるのです。
下図参照

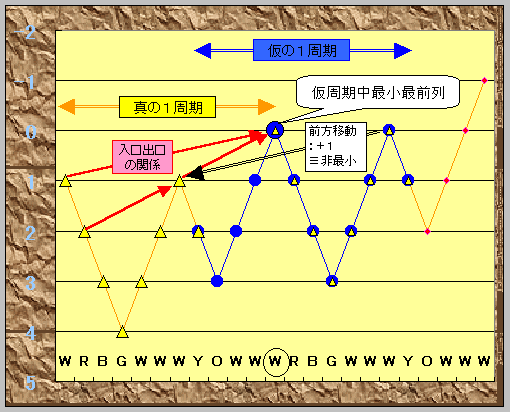
（１）まず、仮の１周期を考え、洞窟の深さが最も浅いところが深さ０になるように相対深さを計算します。
すなわち　仮の入り口から　Ｗなら（−１）、色付なら（＋１）して計算し最小値が０になるように全体を上下させます。
（上図●）　注意）縦軸は通常と逆方向

（２）すると、深さ０の●の中で最初のところが出口となります。

∵（２）で決めた出口から後の部分（小▲部）を前に持ってくると全て、深さが＋１されるので,
結局、真の出口より前では深さが１以上であり、洞窟探検結果として矛盾はありません。

一方、真の出口に対応するところ以外を入り口とすると、
そこから−１した深さの広間
（上図の入口出口の関係→）
に必ず距離で２Ｎ＋１より早く到達します。

ＷやＲＧＢを全くでたらめに置いても、（１）（２）の手順は実行可能です。すなわち、

洞窟の構造と　円上にＷが（Ｎ＋１）個、 Ｎ色の色（Ｒ，Ｇ，Ｂ，Ｙ，Ｏ．．．．）が１個づつ並んだものとが１対１に対応する

のです。
下図参照

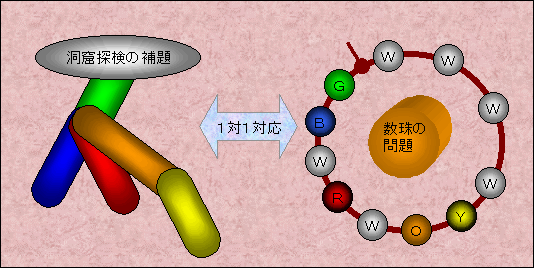
従って、洞窟探検の補題の場合の数はＷを円上に配置し最初のＲ洞窟の位置を適当に決めた後、
のこりＮ−１個をその間間に置いて行く場合の数として計算されます。すなわち

　(Ｎ＋２)×(Ｎ＋３)×・・・・×(２Ｎ)

＝２ＮＰＮ−１

＝

２ＮＰＮ Ｎ＋１

【５つのナップザック】

　「出題者模範解答」と「洞窟探検の補題」とは基本的には同じ構造
（Ｗ：＝ありません）であり異なるところは、

[　ナップザックの中　｜　最も外側　]　のナップザックは順不同である点です。

これはＷとＷの間の洞窟の順序は区別しないのと同じであり、場合の数は直接以下と計算されます。

　(Ｎ＋１)×(Ｎ＋１)×・・・・＜Ｎ−１個の積＞
＝(Ｎ＋１)^N-1

【金太郎飴整列問題】

　「洞窟探検の補題」において最後は必ずＷであるので、これを除き、
Ｗ＝−１　　ＲＧＢ＝１として置き換えれば、「金太郎飴整列問題」と同じです。

すなわち、「金太郎。。」は洞窟の色の区別がない「洞窟探検の補題」と同じです。

　従って　

　「金太郎飴整列問題」

＝	「洞窟探検の補題」 色数Ｎ！

＝

２ＮＣＮ Ｎ＋１

【感想】

　格言をひとつ
「ループを以ってループを制す」 でした。

【出題者のコメント】

「洞窟探険の捕題」による解法、楽しく拝見させて頂きました。
実にみごとでユニークな解法ですね。
いつもながら、借り物ではない独創的な解法には感心します。
私も出来る限り心掛けてはいるのですが、こういった解法が大好きです！
この解法がヒントになって、『金太郎飴整列』の追加問題を創作しました。

◆宮城県　アンパンマン さんからの解答。

各ナップザックを筋点(node)とし,持ち主も別の筋点として考えると
この問題は(n+1)の完全グラフの全域木(spanning tree)の数を求める問題に変わります。
(各全域木、持ち主の筋点を根にして、できた根付き木は「収納の仕方」と1対1対応になります。)

ここで、完全グラフの全域木の数を求める2つの方法を提案します。

方法1)

定理1)

AはグラフGの隣接行列、DはグラフGの次数行列とし、
B＝D-Aとすると、Bの小行列式はグラフGの全域木の数である。

ここで、A={a_u,v},
a_u,v = 1　uv∈E(G)；
a_u,v = 0　uv!∈E(G)

D={d_u,v},
d_u,v　= deg(u)　u=vのとき；
d_u,v　= 0　そのほか。

Gが(n+1)完全グラフのとき、A＝E-I, D=nI
ここで、Eは全ての成分は1である正方行列、I は単位行列です。

つまりB＝(n+1)I-E,

Bの小行列式を計算すると
=(n+1)^n-1＝パッキングの仕方の数

方法2)

根(持ち主)から木の深さとRGBの順で自分がいくつの子を持っているか報告します。
その数をr₀,r₁,r₂,...,r_nとします。
(r₀+r₁+...r_n=n)

ここで、見方を変えて考えてみます。

RGB順なのでr₀のときは選び方が nＣr₀ 通りあります。
r₁のときは n-r₀Ｃr₁ 通りあります。...

つまり(r₀,r₁,...,r_n)になる選び方は

n！ r0！r1！...rn！

で、

合計

＝

Σ ri≧0

n！ r0！r1！...rn！

＝(1+1+...+1)n＝(n+1)n通りです。

しかしこの中に全報告が途中で途切れるケースも含まれています。

途中で途切れないためには(r₀,r₁,...,r_n)は条件1を満たさなければいけない。

条件1)
S(s₀,s₁,s₂,...,s_n)∈{0,1,2,...}ⁿ⁺¹
s₀≧1,
s₀+s₁≧2,
s₀+s₁+s₂≧3
:
s₀+s₁+...+s_n-1≧n
s₀+s₁+...+s_n-1+s_n=n

定理2)

R₁(r₀,r₁,...,r_n-1,r_n)、
R₂(r₁,r₂,r₃,...,r_n,r₀),
R₃(r₂,r₃,...,r_n,r₀,r₁)
:
R_n(r_n,r₀,r₁,...,r_n-1)
の中から、条件1を満たすR_iは2つ以上存在しません。

証明：WLOG,

R₁とR_iが条件1を満たすとすると
r₀+r₁+...+r_i-1≧i

r_i+r_i+1+...+r_n≧n-i+1 より
r₀+r₁+...+r_n≧n+1になり、矛盾

証明終わり

定理3)

R₀,R₁,R₂,...,R_nの中から
必ず条件1を満たすR=R_iが存在する。

証明：

R₀が条件1を満たす場合、R=R₀を選びます。

R₀が条件1を満たさない場合、
j-(r₀+r₁+r₂+...+r_j)が最大になるようなjが一つしかない場合、jより大きい値k、
(r₀+r₁+...+r_k)≧k+1を満たす最小のkをiとすると、
R＝R_iは条件1)を満たします。

j-(r₀+r₁+r₂+...+r_j)が最大になるjが二つ以上存在する場合は、一番小さい値jを選びます。
同じように、jより大きい値k、
(r₀+r₁+...+r_k)≧k+1を満たす最小のkをiとすると、
R＝R_iは条件1)を満たします。
(グラフで表すとすぐわかると思います)

証明終わり

以上定理2)と3)より、
R(r₀,r₁,r₂,...,r_n)のローテーション R₀,R₁,R₂,...,R_nの中から
一つのR_iしか全域木を表せない。

つまり(n+1)完全グラフの全域木の数は

(n+1)n n+1

=(n+1)n-1です。

【出題者のコメント】

完璧です！
完全グラフでのスパニング・ツリーの数と同等だとしたのは流石です。
いろんな解法があるでしょうけど、最も数学的な解法に思えました。

　『５つのナップザック』へ

　数学の部屋へもどる