f(n)=f(x)2+f(y)2=x2+y2=n を得る。
◆東京都 T.Kobayashi さんからの解答。
【問題1】
任意の自然数 n に対して f(n)=n でなければならないことを数学的帰納法を使って証明する。
f(02+02)=f(0)2+f(0)2 ⇔ f(0)(2f(0)-1)=0 で、
f(0) が自然数だから f(0)=0 。
これより f(n2)=f(n)2 を得る。
n=1 を代入すれば、
f(1)=f(1)2 ⇔ f(1)(f(1)-1)=0 で、
f(1)≠0 だから f(1)=1 。
さて、n≦k(≧1) のとき f(n)=n であると仮定して、n=k+1 のときを考える。
(i) n が 4m-1 型の素因数を奇数巾に持たないとき。
このとき、自然数 x, y を用いて n=x2+y2 と書ける。
(複素整数の理論からの帰結)
そして、n≧2 だから x,y≦![]() <n となって、
<n となって、
f(n)=f(x)2+f(y)2=x2+y2=n を得る。
(ii) n が 4m-1 型の素因数を奇数巾に持つとき。
そのような 4m-1 型の素因数のうち最大のものを p と書くことにする。
| p mod 25 | ±1 | ±2 | ±3 | ±4 | ±6 | ±7 | ±8 | ±9 | ±11 | ±12 |
| x | 7 | 11 | 4 | 3 | 8 | 1 | 6 | 12 | 2 | 9 |
上の表によって p の値に対応して x を決めると、
p2+x2≡0 (mod 25) となる。
さらに、p2+x2 は 4m-1 型の素因数を奇数巾に持つことはない。
したがって、自然数 y, z を用いて
p2+x2=(5y)2+(5z)2 と書くことができる。
n=ps とすれば、
n2+(sx)2=(5sy)2+(5sz)2 である。
n2+x2=y2+z2 ならば、両辺に f を作用させて、f の性質から
f(n)2+f(x)2=f(y)2+f(z)2 となり、
f(x)=x, f(y)=y, f(z)=z が分かっていれば、
f(n)2
=f(y)2+f(z)2-f(x)2
=y2+z2-x2
=n2
で、f(n)≧0 から f(n)=n が決定することに注意する。
以降、「f(n) は決定する」と言って「f(n)=n を得る」の意味に使うことにする。
p=3 のとき、(3s)2+(4s)2=(5s)2 である。
このとき、p の最大性により s は 4m-1 型の素因数を奇数巾に持たないから、
4s=a2+b2 、5s=c2+d2 と書ける。
そして s≧1 だから a,b,c,d<n となり、
f(3s)2
=f(c2+d2)2-f(a2+b2)2
=(f(c)2+f(d)2)2-(f(a)2+f(b)2)2
=(c2+d2)-(a2+b2)
=(3s)2
で、f(3s)≧0 から f(3s) が決定する。
p=7 のときは (7s)2+s2=(5s)2+(5s)2 である。
p=11 のときは (11s)2+(2s)2=(5s)2+(10s)2 である。
p=19 のときは (19s)2+(8s)2=(5s)2+(20s)2 である。
f(20s)2=f(400s2)=f((12s)2+(16s)2)=f(12s)2+f(16s)2 だから、
f(19s) は決定する。
p=23 のときは (23s)2+(11s)2=(5s)2+(25s)2 である。
f(25s)2=f(625s2)=f((15s)2+(20s)2)=f(15s)2+f(20s)2 だから、
f(23s) は決定する。
p=31 のときは (31s)2+(8s)2=(20s)2+(25s)2 である。
p=43 のときは (43s)2+s2=(5s)2+(30s)2 である。
p=47 のときは (47s)2+(4s)2=(25s)2+(40s)2 である。
p=59 のときは (59s)2+(12s)2=(5s)2+(60s)2 である。
f(60s)2=f(3600s2)=f((36s)2+(48s)2)=f(36s)2+f(48s)2 だから、
f(59s) は決定する。
p=67 のときは (67s)2+(6s)2=(45s)2+(50s)2 である。
p=71 のときは (71s)2+(3s)2=(45s)2+(55s)2 である。
p≧79 のとき、x≦12 に注意すると、
(ps)2+(sx)2≦(ps)2+(12s)2<(p2+159)s2≦((p+1)s)2
だから、n2+(sx)2=(5sy)2+(5sz)2 において
5sy や 5sz が、ましてや sx が n 以上になることはない。
したがって f(ps) は決定する。
以上まとめると、n≦k(≧1) のとき f(n)=n であると仮定すると、f(k+1)=k+1 が帰結される。
したがって、数学的帰納法の原理により、任意の自然数 n に対して、f(n)=n でなければならない。□
# 複素整数の理論については例えば 高木貞治『初等整数論講義』(共立出版) などを参照のこと。
【問題2】
f(0)=0, f(1)=1 は確定。
2: 2=12+13
5: 5=22+13
8: 8=02+23
12: 12=22+23
27: 27=02+33
10: 12+123=272+103
11: 22+53=112+23
33: 33=52+23
189: 189=82+53
32: 52+103=322+13
6: 02+333=1892+63
7: 62+113=322+73
から、f(7)=7 が確定する。上はコンピュータに追跡させたものである。
手計算でやると、
2: 2=12+13
4: 4=22+03
3: 32+23=42+13
5: 5=22+13
6: 62+03=32+33
10: 10=32+13
11: 112+23=22+53
32: 322+13=52+103
7: 322+73=62+113
からも f(7)=7 が確定する。
コンピュータ検索では、0≦n≦2238 の範囲で n=1379 だけ確定しなかったが、探索範囲を広げれば確定する可能性が高い。
実験から、一般に任意の自然数 n に対して、f(n)=n が成立しそうな気がしますが、証明は思いつきません。
◆出題者のコメント
T.Kobayashi
さん,解答ありがとうございます.
解答は完璧だと思います.
Gaussの整数環Z[i]の性質がうまく活用されていますね.
この方針で行くと,最初からnの最大の素因数pに関する帰納法を用いることもできますね.
いずれにせよ,この問題は一見条件が少ないように思えるのに,
実は恒等写像しかありえないというところが面白いのではないでしょうか.
ところで,問題1には他にも別解があるので,(他の方も含めて)更なる解答をお待ちしています.
(例えば,α = 2q + (q+r)i, β = 2
+ i∈Z[i]に対して,N(αβ) = N(αβ~)を考えると,....)
一方,問題2については,n≦500に対してf(n) = nであることがコンピュータで確認されました.
また問題3については,nが2, 3,
5のみを素因数として持つならば,f(n) = nが成り立つようです.
こちらのほうも引き続き解答(回答)をお待ちしています.
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1解答】
既に解答があるので、f(0)=0,f(1)=1 は確定しているところから始めます。
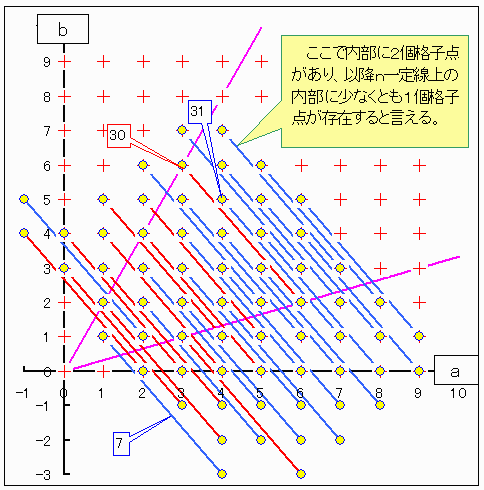
(4a+3b)2+(3a-4b)2=(5a)2+(5b)2は恒等式です。
4と3は互いに素ですから任意のnを正の整数a,bを用いて
n=4a+3bで表すことが複数とおり可能です。
ところでさらに
4a+3b>|3a-4b| & 4a+3b>5a & 4a+3b>5b なる条件をつけます。
これらの条件は 3b>a & b<2a に集約されます。
すると下図に示すように n≧31 においては必ずそのようなaと,bが存在します。
なお赤線と青線は4a+3b=一定(=n)の線です。
つまり f(n)=nがn≦30において確定すれば数学的帰納法によりf(n)=nに限ることが証明されます。
下図において赤線で示される n=1〜6、8、9、10、12、13、15、16、19、20、23、30はこの帰納法が使えないnの値です。
しかしこれらの値に対するf(n)値は 確定しているn=0,1を始めとして、
2=12+12 , 4=22+02, 5=22+12
32=52-42, 72=52+52-12, 8=22+22,
9=32+02, 10=32+12
62=102-82,
11は帰納法, 13=22+32, 122=132-52,
14は帰納法 , 16=42+02 , 152=122+92
17,18は帰納法 , 202=42+22, 192=202+52-82,
21,22は帰納法 , 232=252+52-112
24〜29は帰納法 , 302=242+182
の関係により確定し、f(n)=n for n≦30 です。
よって、一般に f(n)=nです。
【感想】
これは、本当に興味深い現象ですね。
◆出題者のコメント
T.Kobayashi さん,Y.M.Ojisan さん,解答ありがとうございます.
>T.Kobayashi
さん
問題1と同様に問題2でも各nに対してf(n) =
nが順次成り立っていく様子,そしてそれを確定させる方法の(特に手計算での)難しさが,このn=7の例からもお分かりいただけると思います.
コンピュータ検索のほうは,私のよりはるかに確定範囲が広がりましたね.:)
ちなみに,n=7のとき,9ステップ(最短かな?)では次のようなものもあります.
2: 2 = 12 + 13,
3: 32 + 03 =
12 + 23,
4: 4 = 22 + 03,
5: 5
= 22 + 13,
8: 8 = 02 + 23,
10:
10 = 32 + 13,
15: 152 + 03 =
102 + 53,
13: 132 + 43 =
152 + 23,
7: 132 + 73 =
02 + 83.
>Y.M.Ojisan
さん
私が用意していた解答も同様の方法によるものでした.
実は,最初の「恒等式」をうまく選ぶと,
n>12(およびn=11)に対して帰納法の仮定が使えるようになります.
よかったらその方法も考えてみてください.
あと細かいことですが,
>互いに素ですから任意のnを正の整数a,bを用いて表すことが可能
という部分で,a, b≧0に限定すると,『ノートの分配』の問題になるので,
「任意のn≧(4-1)(3-1)=6」になります.
もっとも,その後の議論には差し支えありません.
◆茨城県 こんにちは さんからの解答。
【問題1】
f(n)=nであることを数学的帰納法で示す。
f(0)={f(0)}2+{f(0)}2=2{f(0)}2f(0){2f(0)-1}=0
fは自然数への写像だから、f(0)=0
よって、
f(m2)=f(m2+02)={f(m)}2+{f(0)}2={f(m)}2
となる事がわかる。
m=1を代入してf(1)=f(12)={f(1)}2
f(1)≠0よりf(1)=1である。
f(2)=f(12+12)={f(1)}2+{f(1)}2=1+1=2
f(4)={f(2)}2=22=4
f(5)=f(22+11)={f(2)}2+{f(1)}2=22+1=5
25={f(5)}2=f(25)=f(42+32)={f(4)}2+{f(3)}2=16+{f(3)}2
よって、{f(3)}2=25-16=9=32
f(3)=±3
fは自然数への写像だから、f(3)=3となる。
f(8)=f(22+22)={f(2)}2+{f(2)}2=22+22=8
f(10)=f(32+12)={f(3)}2+{f(1)}2=32+1=10
100={f(10)}2=f(100)=f(62+82)={f(6)}2+{f(8)}2={f(6)}2+64
{f(6)}2=100-64=36
f(6)=±6
fは自然数への写像よりf(6)=6
よって、n≦6のときf(n)=nである事がわかる。・・・・(α)
n≧7のとき(α)より、n≦6では確かにf(n)=nである。
n≦k(kは6以上の自然数)のとき、f(n)=nが成立すると仮定して、
n=k+1のときを考える。
自然数xを以下のように定める
n≡0 (mod 5)のとき、x=0
n≡1 (mod 5)のとき、x=2
n≡2 (mod 5)のとき、x=-1
n≡3 (mod 5)のとき、x=1
n≡4 (mod 5)のとき、x=-2
このように定めるとn2+x2≡0 (mod 5)
2n-x≡0 (mod 5)
n+2x≡0 (mod 5)
となる。
(n2+x2)/5={(2n-x)/5}2+{(n+2x)/5}2
a=(2n-x)/5、b=(n+2x)/5とおくと
(n2+x2)=(a+2b)2+(2a-b)2
a+2b=(4n+3x)/5
a+2b<(4n+n)/5=n
(n>6≧3xだから)
a+2b≧(4n-6)/5>20/5=4
2a-b=(3n-4x)/5
2a-b={(3n+2(-2x)}/5<(3n+2n)/5=n
(n>4≧-2xだから)
2a-b≧(3n-8)/5>10/5=2
{f(n)}2+x2
={f(n)}2+{f(x)}2
=f(n2+x2)
=f({a+2b}2+{2a-b}2)
={f(a+2b)}2+{f(2a-b)}2
=(a+2b)2+(2a-b)2
=n2+x2
{f(n)}2=n2
f(n)=±n
fは自然数への写像だから、f(n)=n
よって、n=k+1のときも、f(n)=nとなる。
よって、数学的帰納法によりn≧7の任意の自然数に対して、f(n)=nである事が示された。・・・(β)
(α)と(β)より、任意の自然数nに対して、f(n)=nが成立する事が示された。
【感想】
きれいな問題だなとあらためて思いました。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題3】
【調査結果】
0を含む自然数の集合をN0で表す。
また0を含む自然数3乗の集合をN03 とする。
基本の関係 :
m,n∈N0 f(m3+n3) = f(m)3+f(n)3 ----(1)
より誘導された関係:
m,n,p,q∈N0,m3+n3=p3+q3 に対し
f(m)3+f(n)3 = f(p)3+f(q)3 ----(2)
はg(x)=f(x)3∈ N03と置くことにより
g(m)+g(n) = g(p)+g(q) ----(2’)
という線形な関係になる。一方(1)は非線形な関係
g(m3+n3) = (g(m) +g(n)) 3 ----(1’)
に置き換わる。
問題1に比べ、(1)の関係や(2)の単独の直列的適用で値が確定するものは非常に少なく、複数の並列関係で決定する必要があるようである。
ある値M以下のnでf(n)を考えるとき、(1)の関係の数に比べ(2)の関係の数の方が圧倒的に多いことがPCによる計算により分かった。
下図参照。
横軸は(2)の関係の数であり、これに対し縦軸は
未知数数:0、1、2、8、9…など容易に確定しているものをMから除いた数
非線形方程式数:m3+n3を含めM以下での(1)の関係の数
不定変数数:M以下での(2)の関係に全く現れない未知数の数
である。
線形方程式に対して未知数の数は0.7乗程度であり、Mが400を超えると線形方程式の数が上回る。
しかし、明確に確定できない不定変数以外にも、方程式の従属性により線型方程式だけで全て決定されることは期待できない。
一方、線形方程式でかなり限定されるとも考えられる。
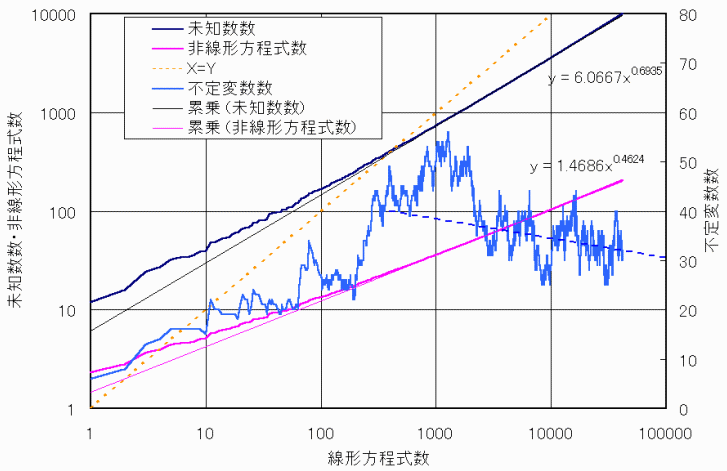
また、非線形方程式の数は0.5乗程度であり、Mが大きくなれば相対的に影響力は小さくなり、やはり線型方程式が大部分の条件を受け持っていると考えられる。
なお不定変数は暫減の傾向にあり、Mが大きくなれば、相対的に0に近づくと予測される。
【f(5)の解答】 f(5)=5
【方針】
調査の結果を踏まえ、PCを用いて効率的にf(n)ないしg(n)の値を決定する方法を次のように定める。
【(2’)の関係】
まず[B]のために、10000未満でm3+n3=p3+q3 (mが最大)であるものをPCで求めた。
計算結果1(lzh圧縮423kbyte)
【[A]の実行】
次の関数値が確定した。g(15)以外は(1’)の関係による。
g(15)は (2’) の関係 163+23=153+93により確定する。
![]()
【[B]の実行】
M=500とする。
この範囲での線形方程式の数は566である。
その線型方程式に全く関わらない不定変数の数は43個であった。
計算結果2(40kbyte)
【[C]の実行】
PCによる有理数値計算の結果、線形方程式のランクは正則値-11であった。
パラメータとして小さい方を優先するロジックで次の11個のパラメータが選ばれた。
![]()
これらをパラメータとした線形方程式の解の全容を計算結果2(40kbyte)にしめす。
【[D]の実行】
さて (1’)の関係より
g(27)=(g(3)+g(0))3=g(3) 3
g(28)=(g(3)+g(1))3=(g(3)+1)3
g(35)=(g(3)+g(2))3=(g(3)+8)3
である。一方線形方程式の解より
g(27)=15g(3)/4-g(4)/4-g(5)/4+39883/2
g(28)=31g(3)/8+3g(4)/8-27g(5)/8+88981/4
g(35)=59g(3)/8-9g(4)/8-55g(5)/8+174429/4
である。
以上からg(3)の3次方程式が得られ、これを解くと実数解は唯一 g(3)=27 である。
即ち、f(3)=3が確定した。
また合わせてg(4)=64 ,g(5)=125 も確定する。
よってf(5)=5である。
計算結果2(40kbyte)を見れば分かるようにg(3),g(4),g(5)が確定するとかなり多くの関数値が確定する。
次にg(13)の確定であるが、g(x)-g(13)=定数 と言うg(13)をいくつかに限定する関係が多数あり、
一般的にはこれらの共通解としてg(13)=133 が決定する。
ただ13の場合、実際には線形方程式解の一つ
g(195)-g(13)=1953-133
を満足するg∈N03の解が1通りしかなく、これだけで決定される。
同様にして g(203),g(286),g(296),g(346)は次の方程式を満足する解の共通解として確定する。
(203) g(371)-g(203)= 3713-2033 と g(488)-g(203)= 4883-2033
(286) g(429)-g(286)= 4293-2863 と g(446)-g(286)= 4463-2863
(296) g(431)+g(296)= 4313+2033 と g(439)+g(296)= 4393+2963
(346) g(463)-g(346)= 4633-3463 と g(428)+g(346)= 4283+3463
g(286)が確定したので 次の関係でg(187)も確定する。
(187) g(396)+g(187)= 3983+1873 と g(426)+g(187)= 4283+1873
残された g(245)とg(461) は 方程式が下記に示す1個ずつしかM=500の範囲では存在しないので、限定されるものの確定できない。
(245) g(382)+g(245)=3823+2453より g(245)= 16 | 245 | 382 | 413
(461) g(500)-g(461)=5003-4613 より g(461)= 124 | 461
以上および(1)の不定変数への再適用から500以下では、
下記を除くnに対してf(n)=n であることが確定する。

【M=9999】
M=500の結果から少なくともn=76までは全部f(n)=nに限ることが分かった。
ところで763=438976 であるので少なくともMx=438976までは、非線型関係は予め使い切ることができ、
線型関係 とg∈N03だけが頼りとなって、問題は単純化される。
もし、438976に達するまでにn=77や143等が確定してゆけば、ずっと最後まで線型関係だけで済む可能性もありうるが、パラメータがどんどん増加する恐れもある。
【[A]の実行】
ところが実際に計算してみると9999以下においては、不定変数の下記32個を除いて、各線形関係の単独の直列的適用だけで全て確定することがPCにより確認された。

M=9999は偶然ながらぎりぎりの値であり、これより少なくすると未知数2に対し方程式が1ぐらいの割合で増加し、方程式を解く必要が出てくる。
一方、少なくともM=10000〜11000の辺りでは、Mを増加させても未知数が出てくることはなく、不定のものだけのようです。
【P。S。】
[A]から[D]のアルゴリズムを繰り返して求めて行くソフトを造ったのですが、Mが大きくなるとそれほど凝らなくても確定してゆくので少し拍子抜けしました。
逆に一般的に解ける可能性が高くなったと思いますので、さらに考えたいと思います。
◆出題者のコメント
こんにちは さん,Y.M.Ojisan さん,解答ありがとうございます.
>こんにちは さん
証明は完璧だと思います.
n>6で帰納法の仮定が使える方法がありましたね.
考え方はすでに出ていたのに,気づきませんでした.;)
ところで,問題1で定義域と値域をともに(負でない)有理数に拡張したらどうなるでしょうか?
問題4.Q+を負でない有理数全体の集合とする.
このとき,次の条件を満たすQ+からQ+への写像fをすべて求めよ.
(a)
f(1)≠0, 1/2,
(b) 任意のx, y∈Q+に対して,f(x2 +
y2) = f(x)2 + f(y)2.
(一応,答えは用意しています.)
>Y.M.Ojisan さん
私も,最初に問題1の「2乗」を「3乗」に拡張したらどうなるか考えたとき,「未知数」の個数より「方程式」の個数が少ないのではないかと思ったので,条件を少し強くするために定義域と値域をともに「整数全体」に拡張しておいたんです!
(どうぞ今一度,問題3をご覧ください.:))
紛らわしい設問の仕方をして申し訳ありませんでした.
ところが,そんな拡張をしなくても,
>Mが400を超えると線形方程式の数が上回る
ではありませんか!(計算結果1参照.)
方程式が従属している場合を考慮しても,上のグラフからも予想されるように,
十分に広い範囲を探索すれば,f(n)の値が順次決まっていきそうですね.
といっても,にわかには信じにくいのですが,例えば,パラメータ表示
| g(6) = | 1 2 | g(3) + | 1 2 | g(4) + | 1 2 | g(5)+ 108 |
ところで,もともとの問題3では,x3 + y3 + z3 =
w3という形の「方程式」も使えるので,
条件が少し強くなります.
この条件の下では,現在のところ以下のことまで分かりました.
次の予想がすべての素数17≦p≦p0に対して成り立つならば,
その素因数がp0より小さいすべての整数nに対してf(n)
= nが成り立つ.
予想.任意の素数p≧17に対して,その素因数がpより小さい整数x, y,
zが存在して,
p3 = x3 + y3 + z3.
特に,上の予想が正しければ,fは恒等写像に限られることが分かります.
なお,上の予想は17≦p<10000に対して成り立つことがコンピュータで確認されました.
◆愛知県 Y.M.Ojisan さんからのコメント
【問題3コメント:g(6)の追跡】
g(6)の追跡を行ったところ g(6)がg(3) g(4) g(5)のみで表されるためにはM=319までが必要でした。
このとき線形方程式は280個ありますが、内1個はg(15)の単独確定に用いられており、連立させるのは279個です。
計算結果を計算結果3(62kbyte)に示します。
今回の計算では係数行列への左操作行列(逆行列もどき)も求め、一部(最初の10行分)を転置して出力(ファイル後半部)しています。
TXTのままでは見にくいのでEXCELをお持ちならCSV形式で読み込んで見てください。
1列目は方程式の識別番号で、計算結果1(lzh圧縮423kbyte) の1列目のデータです。
2列目が問題のg(6)を決めるに必要な方程式の重みです。
0/1のものはg(6)決定に関係ないものとなります。
一方0/1でないものは279個中171個あります。
独立の実数数値計算PRGにより10-16以内で合っていることを検算・確認しました。
これだけの数の方程式からg(6)の式を得るのはPCならではでしょう。
また、関わる未知数は173個であって、方程式の数より多く、g(6)決定用にはセットでしか登場しない組が2組か1組あるようです。
これらから規則性をなにか見つけることに手を付けるパワーは私にはありません。
【問題3コメント:その後分かったこと】
確かに「整数」でしたね。
なんでこれだけf(1)>0なのと思ってはいたのですが、思い込んでしまい見えていませんでした。
注意1行反古いっぱい!
◆愛知県 Y.M.Ojisan さんからの解答。
【問題3解答つづき】
反古にするにはもったいないので、自然数の条件で考えます。
(1)今回、とりあえず非線形な関係は全く用いません。
従ってg(1)=1も確定ではない状態です。
g(0)=0は用います。
このとき同様にM=459までの線形方程式を解くと、計算結果4((114kbyte)の結果が得られ、かなりの部分をg(1)〜g(8)をパラメータとしてそれらの線形結合で確定できることが判ります。
さらにこれを元にしてM=624までの線形方程式を解くとさらにg(13)もg(1)〜g(8)の線形結合で表すことが可能です。
計算結果4(114kbyte)参照。
(M=624まで一気に解いてもよいが、PCの性能上の障壁から分けた)
よって、g(0)〜g(41)がg(1)〜g(8)をパラメータとして確定するので、M=9999までの線形方程式を解くと、先回の解答に示した除外値 g(5317)・・・を除いて9999までをg(1)〜g(8)の線形結合で表すことが可能です。
さて
k3=Ak*13 +Bk*23+Ck*33+Dk*43+Ek*53+Fk*63+Gk*73+Hk*83
の関係が、相当数分ったわけですが、特に
k=2*(8*3*5*7)=1680 , 3*(8*3*5*7)=2520 ,
5*(8*3*5*7)=4200 , 7*(8*3*5*7)=5880
の関係が判ったことは重要です。
いま、 n=2p3q5r7s
p≦P+2 , q≦Q , r≦R , s≦S に対するg(n)が全て確定しているとします。
m=2P-13Q-15R-17S-1 , V=2P+23Q5R7S とおくとき
(2V)3 =(1680m)3 =A1680*m3+B1680*(2m)3+C1680*(3m)3+D1680*(4m)3+E1680*(5m)3+F1680*(6m)3+G1680*(7m)3+H1680*(8m)3であって右辺に対応のg()は全部確定値です。
即ち、Pは数学的帰納法により無限大に拡張されます。
同様に (3V)3=(2520m)3 よりQが無限大に、
(5V)3=(4200m)3 よりRが無限大に、
(7V)3=(5880m)3 よりRが無限大に拡張されます。
P=Q=R=S=1とするとV最大=840ですが、先回の解答から
これらはg(n)=n3であると確定しています。
よって少なくともnが2と3と5と7だけを因数にもつ自然数ならg(n)=n3
すなわちf(n)は恒等変換です。
(2)さて、 5317 5629 7007は素数ではありません。
従って先回の解答より8689未満の素数kは
k3= Ak*13+Bk*23+Ck*33+Dk*43+Ek*53+Fk*63+Gk*73+Hk*83
の関係で表されたわけです。
N0(k,L)をk未満の素因数(任意乗)とL未満乗の素因数kだけをもつ自然数全体とします。
z∈N0(k,L) に対して
(zk)3=Ak*z3 +Bk*(2z)3+Ck*(3z)3 +Dk*(4z)3+Ek*(5z)3+Fk*(6z)3+Gk*(7z)3+Hk*(8z)3
です。
右辺は全てN0(k,L)の要素ですが、左辺はN0(k,L+1の)要素です。
よって数学的帰納法よりN0(k,∞)=Z(kの次の素数、0)において
g(n)=n3であるといえました。
さらに、k方向の数学的帰納法により N0(8689の前の素数,0)において
g(n)=n3であることが証明されました。
(3)8689以上の素数を因数に持つ場合ですが、\aleph_0 さんの予想と同様で若干条件の強い条件の次の予想が常になりたてば、
(2)の手法により一般にg(n)=n3
即ちf(n)は恒等変換であるといえます。
【予想】
∀W∈{:8689以上の素数},∃X,Y,Z∈N0(W,0)
W3=−X3+Y3+Z3
なお,上の予想は41と47を除く 17≦W<20000 に対して成り立つことがコンピュータで確認されました.
計算結果5(69kbyte)参照。
よってf(n)=n 、 n∈N0(19997,∞)が確定しました。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題4解答】
【定義】
| Gd(n)=f( | n d2 | ) | 2 | ,n∈非負整数,d∈自然数 |
【ZEROの補題】
Gd(0)=0 である。
∵
x=0、y=0の場合 f(0)=2*f(0)2である。
| よってf(0)=0 | | 1 2 | である。 |
x=0、y=1の場合を考えると f(1)= f(1)2+f(0)2である。
f(0)=0の場合 f(1) ≠0なので f(1)=1である。
| f(0)= | 1 2 | の場合f(1)= | 1 2 | であるがf(1)≠ | 1 2 | なので解ではない。 |
【コンニチワさんの補題】
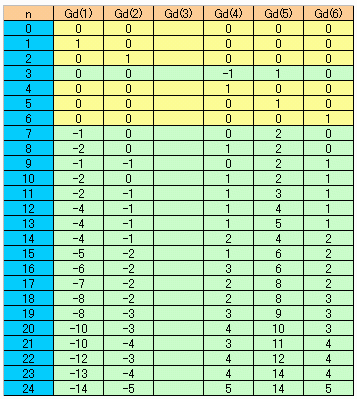
任意のGd(n) は Gd(1) Gd(2) Gd(4) Gd(5) Gd(6) の定係数線形結合で表すことができる。
∵
(1) 32+42=52+0 であるから
Gd(3)+Gd(4)=Gd(5)+ Gd(0) である。
即ちGd(3)=Gd(5)+ Gd(0)−Gd(4)=Gd(5)−Gd(4)
(2) こんにちわさんの解答より
∀n>6 ∃a,b,c<n ∈非負整数 において下記が成立している。
n2=a2+b2-c2
したがって、Gd(n)= Gd(a)+Gd(b)- Gd(c) である。
n未満のGd()において補題が成立してれば、それらGd(a),Gd(b),Gd(c)の線形結合であるGd(n)でも数学的帰納法により成立する。
実際に(1)によりGd(1)〜Gd(6)はGd(1) Gd(2) Gd(4) Gd(5) Gd(6)で表されている。
従って補題は証明された。
下表にn=24までの実際の係数をPCで求めたものを示す。
【自然数の補題】
G1(n)=n2 (n∈自然数) である
ZEROの補題より G1(0)=0 、G1(1)=f(1)2=1 である。
以降【問題1】と同じ証明が可能である。
よってG1(n)=n2 である。
【本編解答】
| Gd(n)= | n2 d4 | を示すことにより |
| 1 d2 | =( | d d2 | ) | 2 |
| 2 d2 | =( | d d2 | ) | 2 | +( | d d2 | ) | 2 | である。 |
| 従ってf( | 1 d2 | )=f( | d d2 | ) | 2 | などより |
すなわち Gd(2)=4Gd(1) である。
Gd(d)=0の場合はGd(1)=Gd(2)=0として含まれる。
| 同様に | k2 d2 | =( | kd d2 | ) | 2 |
| 2k2 d2 | =( | kd d2 | ) | 2 | +( | kd d2 | ) | 2 |
k=2: Gd(8)=2Gd(4), k=3: Gd(18)=4Gd(9)
| また、 | 5 d2 | =( | d d2 | ) | 2 | +( | 2d d2 | ) | 2 | より |
計算すると
Gd(5)=Gd(d) 2+2*Gd(d)*Gd(2d)+Gd(2d) 2=Gd(1)+Gd(4)+ 2*Gd(d)*Gd(2d)
移項して2乗すると
(Gd(5)-Gd(1)-Gd(4))2=4*Gd(1)*Gd(4)である。
以上およびコン二チワさん補題を組み合わせると下記2次方程式系が得られる。
(未知数8個 式7個)

1の系列は Gd(n)=n2S (n=1〜6) になっており、
コン二チワさんの補題から一般にGd(n)=n2Sである。
n=d2を代入すると 自然数の補題より
Gd(d2)= G1(1)=f(1)2=1であるので
| S= | 1 d4 | である。 |
| よって Gd(n)= | n2 d4 | であり、 |
| f( | n d2 | )≧0であるからf( | n d2 | )= | n d2 |
2の系列は Gd(n)=0 (n=0、4、8) が特徴である。
さらにコン二チワさんの補題を用いて n=12、16、20、24を計算すると全て0である。
一方、m= d2を代入すると 自然数の補題より
Gd(4d2)=G1(4)=f(4) 2=16でありGd(4m)=0と矛盾する。
よって系列2は成立しない。
以上で f(n)はQ+においても「恒等変換」のみであることが示された。
【感想】
なんとも不思議なくらい絶妙にできていますね。
かなりのレベルで名問題と思います。
◆出題者のコメント
Y.M.Ojisan,解答ありがとうございます.
まず問題4ですが,方針はOKだと思います.
なお,私が用意した解法は,
任意のn∈N,
x∈Q+に対してf(nx) =
nf(x)であることを示すものでした.
ということで,こちらも引き続き解答をお待ちしています.
次に問題3についてですが,すでに指摘されているように,
問題1や3でf(n)の値を求めるには「線形の関係」と「非線形の関係」を用いる方法があります.
私も「線形の関係」に注目して,少し一般化して次のような考察をしてみました.
Kを体とし,正の整数kに対してVkをZからKへの関数uで次の条件を満たすものの集合とします.
(a) u(0) = 0,
(b) m, n, p, q∈Zに対して,mk +
nk = pk + qkならば,
u(m) + u(n) = u(p) + u(q).
このとき,Vkは自然な加法およびスカラー倍によりK上のベクトル空間になることが分かります.
また,kが偶数または奇数に応じて,
任意のu∈Vkは偶関数または奇関数になることに注意します.
まずk = 1のときは,dimK V1 =
1,
すなわちV1はベクトル空間としてKと同形になることが分かります.
次にk = 2のときは,Kの標数が2, 3, 5でなければ,
dimK V2 =
5になります.
そこで,「コンニチワさんの補題」は最良の評価であることが分かります.
k = 3のときは,Kの標数が3, 7, 13, 19でなければ,
dimK
V3≧7になります.
一方,計算結果4からは,dimK V3≦7
(特に有限次元)になると推測できます.
(今は定義域がZなので,
任意のu∈V3に対してu(3) +
u(4) + u(5) = u(6)となることに注意.)
そして,
予想2.char K≠3, 7, 13, 19のとき,dimK V3 = 7.
が正しければ,問題3のfは恒等写像であることが証明できます.
なお,Y.M.Ojisanが示されたのと同様の方法により,予想2は予想1から従うことが分かります.
k≧4のときは,dimK Vkはどうなるのでしょうか?
上の条件(b)の仮定を満たすようなm, n,
p,
q∈Zが存在しなければ,当然無限次元になります.
k≧5のときは,そのような組は発見されていないようです.
k =
3, 4辺りが一番面白そうですね.