◆広島県 清川 育男 さんからの解答。
【問題1】
とりあえずプログラムを組んで規則性を探って見ました。1) 0 0 0 1 0 1 1 1
000 (0)
001 (1)
010 (2)
101 (5)
011 (3)
111 (7)
110 (6)
100 (4)
中 略
8) 1 1 1 0 1 0 0 0
111 (7)
110 (6)
101 (5)
010 (2)
100 (4)
000 (0)
001 (1)
011 (3)
(4,0,1),(3,7,6) はセットのようです。
(2,5)または(5,2)が挿入的に入るようです。
【問題2】
大分規則性が見えてきました。
1) 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1
2) 0 0 0 0 1 0 0 1 1 1 1 0 1 0 1 1
3) 0 0 0 0 1 0 1 0 0 1 1 0 1 1 1 1
中 略
255) 1 1 1 1 0 1 1 0 0 0 0 1 0 1 0 0
256) 1 1 1 1 0 1 1 0 0 1 0 1 0 0 0 0
省略なしの全文はこちらです。
◆神奈川県 数楽者 さんからのコメント。
この問題の解は、数字のずらしと反転に対して不変です。
つまり、ある解系列に対して、その数字をずらした系列や、数字の順を逆にした系列も解になっています。
その意味で、これらの解はすべて同じものと考えられます。
何らかの意味で解の表現に気を付ける必要があります。
たとえば、「解の代表元は2進数で最小のものとする」などです。
◆広島県 清川 育男 さんからの解答。
数楽者さんからのコメントにしたがって重複を排除しました。
【問題1】
1) 0 0 0 1 0 1 1 1
2) 0 1 0 0 0 1 1 1
3) 0 1 0 1 1 1 0 0
4) 0 1 1 1 0 1 0 0
【問題2】
1) 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1
2) 0 0 0 0 1 0 0 1 1 1 1 0 1 0 1 1
3) 0 0 0 0 1 0 1 0 0 1 1 0 1 1 1 1
4) 0 0 0 0 1 0 1 0 0 1 1 1 1 0 1 1
5) 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1
6) 0 0 0 0 1 0 1 1 0 1 0 0 1 1 1 1
7) 0 0 0 0 1 0 1 1 1 1 0 0 1 1 0 1
8) 0 0 0 0 1 0 1 1 1 1 0 1 0 0 1 1
9) 0 0 0 0 1 1 0 0 1 0 1 1 1 1 0 1
10) 0 0 0 0 1 1 0 1 0 0 1 0 1 1 1 1
11) 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 1
12) 0 0 0 0 1 1 0 1 1 1 1 0 0 1 0 1
13) 0 0 0 0 1 1 1 1 0 0 1 0 1 1 0 1
14) 0 0 0 0 1 1 1 1 0 1 0 0 1 0 1 1
15) 0 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1
16) 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1
17) 0 0 1 0 0 0 0 1 1 0 1 0 1 1 1 1
18) 0 0 1 0 0 0 0 1 1 1 1 0 1 0 1 1
19) 0 0 1 0 1 0 0 0 0 1 1 0 1 1 1 1
20) 0 0 1 0 1 0 0 0 0 1 1 1 1 0 1 1
21) 0 0 1 0 1 1 0 0 0 0 1 1 1 1 0 1
22) 0 0 1 0 1 1 0 1 0 0 0 0 1 1 1 1
23) 0 0 1 0 1 1 1 1 0 0 0 0 1 1 0 1
24) 0 0 1 0 1 1 1 1 0 1 0 0 0 0 1 1
25) 0 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1
26) 0 0 1 1 0 1 0 0 0 0 1 0 1 1 1 1
27) 0 0 1 1 0 1 0 1 1 1 1 0 0 0 0 1
28) 0 0 1 1 0 1 1 1 1 0 0 0 0 1 0 1
29) 0 0 1 1 1 1 0 0 0 0 1 0 1 1 0 1
30) 0 0 1 1 1 1 0 1 0 0 0 0 1 0 1 1
31) 0 0 1 1 1 1 0 1 0 1 1 0 0 0 0 1
32) 0 0 1 1 1 1 0 1 1 0 0 0 0 1 0 1
33) 0 1 0 0 0 0 1 0 1 1 0 0 1 1 1 1
34) 0 1 0 0 0 0 1 0 1 1 1 1 0 0 1 1
35) 0 1 0 0 0 0 1 1 0 0 1 0 1 1 1 1
36) 0 1 0 0 0 0 1 1 0 1 1 1 1 0 0 1
37) 0 1 0 0 0 0 1 1 1 1 0 0 1 0 1 1
38) 0 1 0 0 0 0 1 1 1 1 0 1 1 0 0 1
39) 0 1 0 0 1 0 1 1 0 0 0 0 1 1 1 1
40) 0 1 0 0 1 0 1 1 1 1 0 0 0 0 1 1
41) 0 1 0 0 1 1 0 0 0 0 1 0 1 1 1 1
42) 0 1 0 0 1 1 0 1 1 1 1 0 0 0 0 1
43) 0 1 0 0 1 1 1 1 0 0 0 0 1 0 1 1
44) 0 1 0 0 1 1 1 1 0 1 1 0 0 0 0 1
45) 0 1 0 1 1 0 0 0 0 1 0 0 1 1 1 1
46) 0 1 0 1 1 0 0 1 0 0 0 0 1 1 1 1
47) 0 1 0 1 1 1 1 0 0 0 0 1 0 0 1 1
48) 0 1 0 1 1 1 1 0 0 1 0 0 0 0 1 1
49) 0 1 1 0 0 0 0 1 0 0 1 1 1 1 0 1
50) 0 1 1 0 0 0 0 1 0 1 0 0 1 1 1 1
51) 0 1 1 0 0 0 0 1 1 1 1 0 1 0 0 1
52) 0 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1
53) 0 1 1 0 0 1 0 1 0 0 0 0 1 1 1 1
54) 0 1 1 0 0 1 1 1 1 0 1 0 0 0 0 1
55) 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 1
56) 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 1
57) 0 1 1 1 1 0 0 0 0 1 0 0 1 1 0 1
58) 0 1 1 1 1 0 0 0 0 1 0 1 0 0 1 1
59) 0 1 1 1 1 0 0 0 0 1 1 0 1 0 0 1
60) 0 1 1 1 1 0 0 1 0 0 0 0 1 1 0 1
61) 0 1 1 1 1 0 0 1 0 1 0 0 0 0 1 1
62) 0 1 1 1 1 0 0 1 1 0 1 0 0 0 0 1
63) 0 1 1 1 1 0 1 0 0 0 0 1 1 0 0 1
64) 0 1 1 1 1 0 1 0 0 1 1 0 0 0 0 1
【問題3】
1) 0 0 0 0 1 0 0 1 1 1
2) 0 0 0 0 1 0 1 1 0 1
3) 0 0 0 0 1 0 1 1 1 1
4) 0 0 0 0 1 1 0 1 1 1
5) 0 0 0 0 1 1 1 0 0 1
6) 0 0 0 0 1 1 1 0 1 1
7) 0 0 0 0 1 1 1 1 0 1
8) 0 0 0 1 0 0 1 1 1 0
9) 0 0 0 1 0 0 1 1 1 1
10) 0 0 0 1 0 1 0 0 1 1
11) 0 0 0 1 0 1 1 0 1 0
12) 0 0 0 1 0 1 1 1 0 1
13) 0 0 0 1 0 1 1 1 1 0
14) 0 0 0 1 1 0 0 1 0 1
15) 0 0 0 1 1 0 1 1 1 0
16) 0 0 0 1 1 0 1 1 1 1
17) 0 0 0 1 1 1 0 0 1 0
18) 0 0 0 1 1 1 0 1 1 0
19) 0 0 0 1 1 1 1 0 0 1
20) 0 0 0 1 1 1 1 0 1 0
21) 0 0 0 1 1 1 1 0 1 1
22) 0 0 1 0 0 0 0 1 1 1
23) 0 0 1 0 0 0 1 1 1 1
24) 0 0 1 0 0 1 1 1 0 0
25) 0 0 1 0 0 1 1 1 1 0
26) 0 0 1 0 1 0 0 0 1 1
27) 0 0 1 0 1 0 0 1 1 0
28) 0 0 1 0 1 1 0 1 0 0
29) 0 0 1 0 1 1 1 0 1 0
30) 0 0 1 0 1 1 1 1 0 0
31) 0 0 1 0 1 1 1 1 0 1
32) 0 0 1 1 0 0 0 1 0 1
33) 0 0 1 1 0 0 1 0 1 0
34) 0 0 1 1 0 1 0 1 1 1
35) 0 0 1 1 0 1 1 1 0 0
36) 0 0 1 1 0 1 1 1 1 0
37) 0 0 1 1 1 0 0 0 0 1
38) 0 0 1 1 1 0 0 1 0 0
39) 0 0 1 1 1 0 1 0 1 1
40) 0 0 1 1 1 0 1 1 0 0
41) 0 0 1 1 1 1 0 0 0 1
42) 0 0 1 1 1 1 0 0 1 0
43) 0 0 1 1 1 1 0 1 0 0
44) 0 0 1 1 1 1 0 1 1 0
45) 0 1 0 0 0 0 1 0 1 1
46) 0 1 0 0 0 0 1 1 1 0
47) 0 1 0 0 0 0 1 1 1 1
48) 0 1 0 0 0 1 0 1 1 1
49) 0 1 0 0 0 1 1 0 0 1
50) 0 1 0 0 0 1 1 1 1 0
51) 0 1 0 0 1 0 1 1 1 1
52) 0 1 0 0 1 1 0 0 0 1
53) 0 1 0 0 1 1 1 0 0 0
54) 0 1 0 0 1 1 1 1 0 0
55) 0 1 0 1 0 0 0 1 1 0
56) 0 1 0 1 0 0 1 1 0 0
57) 0 1 0 1 1 0 0 1 1 1
58) 0 1 0 1 1 0 1 0 0 0
59) 0 1 0 1 1 1 0 0 1 1
60) 0 1 0 1 1 1 0 1 0 0
61) 0 1 0 1 1 1 1 0 0 0
62) 0 1 0 1 1 1 1 0 1 0
63) 0 1 1 0 0 0 0 1 1 1
64) 0 1 1 0 0 0 1 0 1 0
65) 0 1 1 0 0 0 1 1 1 1
66) 0 1 1 0 0 1 0 1 0 0
67) 0 1 1 0 0 1 1 1 0 1
68) 0 1 1 0 1 0 0 0 0 1
69) 0 1 1 0 1 0 1 1 1 0
70) 0 1 1 0 1 1 1 0 0 0
71) 0 1 1 0 1 1 1 1 0 0
72) 0 1 1 1 0 0 0 0 1 0
73) 0 1 1 1 0 0 0 0 1 1
74) 0 1 1 1 0 0 1 0 0 0
75) 0 1 1 1 0 0 1 1 0 1
76) 0 1 1 1 0 1 0 0 0 1
77) 0 1 1 1 0 1 0 1 1 0
78) 0 1 1 1 0 1 1 0 0 0
79) 0 1 1 1 1 0 0 0 0 1
80) 0 1 1 1 1 0 0 0 1 0
81) 0 1 1 1 1 0 0 0 1 1
82) 0 1 1 1 1 0 0 1 0 0
83) 0 1 1 1 1 0 1 0 0 0
84) 0 1 1 1 1 0 1 0 0 1
85) 0 1 1 1 1 0 1 1 0 0
問題1と問題3は重複の対応が単純ですが、問題2のそれは複雑です。◆広島県 清川 育男 さんからの解答。
【問題4】
| N=2 | 0 0 1 1 |
| N=3 | 0 0 0 1 0 1 1 1 |
| N=4 | 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 |
| N=5 | 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1 |
N=6 が解れば、規則性がつかめるのですが、、、。
◆広島県 清川 育男 さんからの解答。
【問題4】
2n個の半分が0、残り半分は1でなければならない。
n=6 |000000|100001|100010|100011|100100|101100|110100|111101|101110|1010|111111|
1 2 3 4 5 6 7 8 *
n=6の場合が解ってn個の0,1の並びのパターンの規則性は、ペアで考えると存在するような気がするのですが、、、。◆広島県 清川 育男 さんからの解答。
【問題4】
方法と言えるもか自信がありませんが、必ず出来ると思います。
一般式として表現するにはかなりの困難が予想されます。
N=7 の場合を例に説明します。
27=128
128個の0−127の数字の並びを作ります。
0,1,2,4,8,16,32,65,... ,63,127,126,124,120,112,96,64
「...」の部分の数を決めることになる。
1000001 →65
000001□
□に0,1を入れることになるが、すでに使われているものを排除し、小さい方を選ぶ。
すなわち0を当てはめる。
したがって、
000001□ →0000011 となる。
000011□ →0000110
最初に固定した数字にもあてはまることであるが、
前者×2=後者 または 前者×2+1=後者 の規則が現れる。
......
0110000 48
1100001 97
1000010 66
0000101 5
最後につなぎ合わせれば出来上がり。
プログラムを組めば対応出来ますが、一般的表現は解りません。
◆東京都 未菜実 さんからの解答。
N=4以降は解答が複数有り、しかもその解の数は急激に増加するようです。
N≧6 は解の数の把握さえ困難です。
N=2
1 0011
N=3
1 00010111
N=4
1 0000100110101111
2 0000100111101011
3 0000101001101111
4 0000101001111011
5 0000101100111101
6 0000101101001111
7 0000101111010011
8 0000110100101111
N=5
1 00000100011001010011101011011111
2 00000100011001010011101101011111
・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・
1023 00000111011010100010011001011111
1024 00000111011010100110010001011111
N=6
1 0000001000011000101000111001001011001101001111010101110110111111
2 0000001000011000101000111001001011001101001111011011101010111111
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
N=7
1 00000001000001100001010000111000100100010110001101000111100100110010101001011100110110011101001111101010110101111011011101111111
2 00000001000001100001010000111000100100010110001101000111100100110010101001011100110110011101001111101010110101111011101101111111
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
N=8
1 0000000010000001100000101000001110000100100001011000011010000111100010001001100010101000101110001100100011011000111010001111100100101001001110010101100101101001011110011001101010011011100111011001111010011111101010101110101101101011111011011110111011111111
2 0000000010000001100000101000001110000100100001011000011010000111100010001001100010101000101110001100100011011000111010001111100100101001001110010101100101101001011110011001101010011011100111011001111010011111101010101110101101101011111011101111011011111111
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ ◆出題者のコメント
皆さん解答ありがとうございます。
【問題4】は清川さんの方法で多分全部できると思われますが、全て尽くせるのか、最後がうまくつながるのか明確ではありません。
似たような数列にはなりますが、数値として小さい物からではなく、1のたっているビット数が小さいものから詰めてゆく方法とすると証明しやすいと思います。
○n=6の場合を具体例に、ひとつの方法を示します。
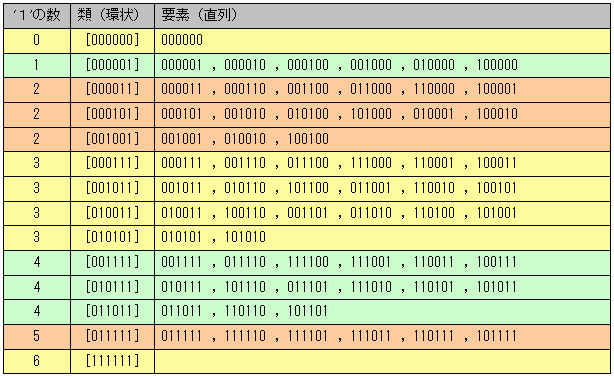
26=64個の直列ビットパターンを環状にしたときのビットパターンで分類すると下表のように14類に分類できます。
この類をその代表元xxxxxxを用いて[xxxxxx]で表すことにします。

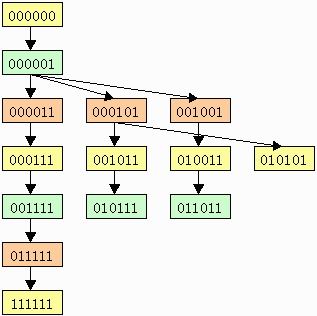
次に分類した類の集合に関係→で木リスト状の構造を与えます。
ここでA→Bは類Aの’1’の数より類Bの’1’の数が一つ多くてかつ環状パターンでのパターンの相違が一箇所だけであることです。
この矢印により[000000]を基点として全ての類を木リスト状に結合することが可能です。
下図参照。構造は必ず1とおり以上あります。
(yyyyyyyy)はビットパターンyyyyyyyyを環状ビットパターンとしたときに現れる連続nビットの直列ビットパターンの集合とすると、
(0000001)=[000000]+[000001] であることは容易に分かります。
いま(X)⊃[A] [A]→[B] であるとします。
[A]→[B]であるので
[A]∋∃aaaaa0 [B] ∋∃aaaaa1 aaaaaは5ビットのパターン
つまり右端のビットだけ異なる[A]と[B]の要素が必ず存在します。
また(X)⊃[A] なので(X)∋aaaaa0です。
このaaaaa0の部分は下図のように[B]+aaaaa0に置き換えることが可能であり、
(Y)=(X)+[B]を作成することが可能です。
ただし[b]の要素数がnより少ない場合はその個数は必ずnの約数であり,
最小の周期パターンであるaa1とかa1だけを追加します。
<例> 011010→[B]=[011011] 要素3個 は aa1=011
(X)=(0000001)を開始点として、作成した木リストの構造に沿って上記操作を繰り返すことにより、 全ての要素を含むビットパターンを作ることが可能です。
なお、木リストの端末や側鎖の構造は必ずしも追加しなくてもよいので、
2n 以外の周期のパターンも大抵作れるようです。
(X)=****************aaaaa0***********
(Y)=****************aaaaa1aaaaa0************
○ n=4のとき木リストは
(1) 主鎖 [0000]→[0001]→[0011]→[0111]→[1111] 側鎖 [0001]→[0101]
(2) 主鎖 [0000]→[0001]→[0101]→[0111]→[1111] 側鎖 [0001]→[0011]
の2通りで、
[0001]→[0011] のaaa0→aaa1 として 0010→0011 1000→1001 の2通り
[0001]→[0101] のaaa0→aaa1 として 0100→0101 の1通り
[0101]→[0111] のaaa0→aaa1 として 1010→1011 の1通り
[0011]→[0111] のaaa0→aaa1 として 0110→0111 1100→1101 の2通り
これらの組み合わせからは、未菜実さん解答の8通りのうちの3通りが得らるだけで、一つの方法に過ぎないことが分かります。
M系列から作るともっとランダムな系列として得ることができますが、一般に存在するという証明は困難のようです。
○ 関連問題として「系列M2をまわせ」を作りましたので考えてみてください。