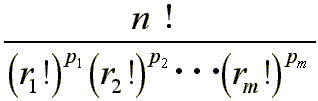『同順を許す並び方の数は？』解答

◆宮城県　アンパンマン さんからの解答。

kグループ1,2,..,kの順番で到着するとします。
各グループの数はr1,r2,...,rk (≧1)とします。
(r1+r2+...+rk=n)

そのとき、並び方は
n！
r1！r2！...rk！		通りです。

kグループの中に同じ数があるとします。
つまりr1人のグループがp1グループあります。
r2人のグループがp2グループあります。
...

rm人のグループがpmグループあります。
p1+p2+...+pm=k, riはすべて異なる(≧1)。
p1*r1+p2*r2+...+pm*rm=n

グループの順番を考えると

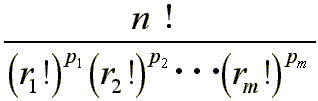通りあります。

以上より、ゴールする順番は

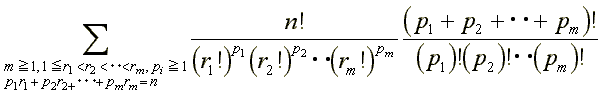通りあります。

n=2,
2！
1！1！		+2！
2！		=3 通り

n=3,
3！
1！1！1！		+3！
2！1！		*2C1 +3！
3！		=13 通り

n=4,
4！
1！1！1！1！		+4！
2！2！		+4！
2！1！1！		*3C1 +4！
3！1！		*2C1 +4！
4！		=75通りです。

◆愛知県　Y.M.Ojisan さんからの解答。

解答が既にありますが、さらに計算量の節約を考えてみます。

【定義】

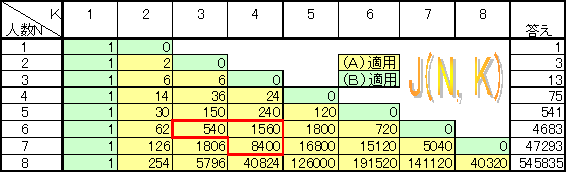
　Ｊ（Ｎ，Ｋ）を　Ｎ人競争の結果の内，グループ数がＫである場合の組み合わせ数とします。

【漸化式】

このとき、次の漸化式が成立します。

　Ｊ(Ｎ，Ｋ)＝Ｋ×｛Ｊ(Ｎ−１，Ｋ―１)＋Ｊ(Ｎ−１，Ｋ)｝――(Ａ)
　Ｊ(Ｎ，１)＝１　、Ｊ(Ｎ，Ｎ＋１)＝０　　　　　　　　　――(Ｂ)
∵Ｊ(Ｎ，Ｋ)における、ゼッケンＮの人の状態を考えると、大きく

(１)単独である場合と、(２)仲間がいる場合の２つに分けられます。

(１)の場合、ゼッケンＮの人がいない場合の組み合わせは、人とグループがそれぞれ１減るので
Ｊ(Ｎ−１，Ｋ−１)であり、一方、ゼッケンＮの人が居た場所は植木算でＫ箇所あります。

(２)の場合、ゼッケンＮの人がいない場合の組み合わせは、人だけ１減るので
Ｊ(Ｎ−１，Ｋ)であり、一方、ゼッケンＮの人が居た場所はＫ箇所あります。

よって(Ａ)式が成立します。(Ｂ)は自明です。

【答え】

従って総数は

　 N

k=1		Ｊ（Ｎ，Ｋ）

【計算量】

Ｎ−１人からＮ人の場合を計算する場合、（Ａ）式は　Ｎ−１回適用されます。
従って全計算量はＮの２次式のオーダーとなり計算機で計算可能な程度です。

因みにアンパンマンさんの方法では　各項計算量はＮの一次ですが、狽ﾌ項数が『果物の分配』問題での
Ｓ（Ｎ）個あり、ＮＰ問題のようです。

【計算結果】

８人までの結果を以下に示します。

【感想】

　何かうまい方法があって、Ｎの一次式の程度の計算量の方法があるのでしょうか　？。

◆出題者のコメント。

お二人とも、みごと正解です。
問題と直接がっぷり４つに組んでの解法と、「漸化式」による解法、それぞれの持ち味が出ていたように思えます。
それにしても、漸化式(Ａ)を、よく発見したものですね。
私には無理でした。(^^;

出題後に、パスカルの三角形を利用した面白い解法を発見しましたので紹介します。

パスカルの三角形から１番右端の（１）は取り去ります。
左端から右に、偶数番目の数に（−１）を掛けます。
（図ではマイナスは赤色で表します）


　　　　１　１　　　　　　　　　　　１　　　　　←１段目
　　　１　２　１　　　　→　　　　１　２　　　　←２段目
　　１　３　３　１　　　　　　　１　３　３　　　←３段目
　１　４　６　４　１　　　　　１　４　６　４　　←４段目
　　　　　：　　　　　　　　　　　　：
Ｎ人の時は、このパスカルの三角形の上からＮ段目までの数字をすべて使用しますが、ここでは、４人の時を例にして説明します。

まず、各段目の左端から右斜め下に順々に表示されている数字をすべて加えます。 

　　　　　　　　１　　　　　　　　　←１段目
　　　　　　　１＼２　　　　　　　　←２段目
　　　　　　１＼３＼３　　　　　　　←３段目
　　　　　１＼４＼６＼４　　　　　　←４段目
　　　　──────────
　　　　　　 １＼３＼４＼２　　　　 ←合計段
次に、この合計段の数の左から順に４4,３4,２4,１4を掛け、すべてを加えます。
　１*４4−３*３4＋４*２4−２*１4
＝２５６−２４３＋６４−２
＝７５
以上です。

一般にＮ人の時の同順を許す並び方の数ｆ(Ｎ)を、

ｆ(N)＝Kn*NN＋Kn-1*(N-1)N＋・・・＋K2*2N＋K1*1N

と表した時、面白いことにパスカルの三角形より得た合計段の数字が、式の同位置の各項の係数になります。
（Kn、Kn-1、・・・、K2、K1 は各項の係数です）

指数型母関数
[指数型計数子： x1
1！		+x2
2！		+x3
3！		 + …] による解法で、
ｆ(N)＝ N

i=1		 i-1

j=0		{iＣj*(-1)j*(i-j)N}

を得(計算省略)、これを変形して
ｆ(N)＝ N

i=1		 N-i

j=0		{(-1)j*i+jＣj*iN}

この式を眺めているうちに、パスカルの三角形による解法を発見しました。

◆宮城県　アンパンマン さんからの解答。

Y.M.Ojisan さんの漸化式より
F(x,y)= ∞

n=0,k=0		J(n,k)xn yk を定義します。

∞

n=1
k=1		J(n,k)xn yk
= ∞

n=1
k=1		(k)J(n-1,k-1)xn yk + ∞

n=1
k=1		k J(n-1,k)xn yk
= ∞

n=1
k=1		(k-1)J(n-1,k-1)xn yk + ∞

n=1
k=1		J(n-1,k-1)xn yk + ∞

n=1
k=0		k J(n-1,k)xn yk

F(x,y)- ∞

n=0
 J(n,0)xn - ∞

k=1		J(0,k) yk
=xy2 δF(x,y)
δy		+xyF(x,y)+xy δF(x,y)
δy

J(n,1)=J(n-1,0)+J(n-1,1) とJ(1,1)=J(0,0)+J(0,1) より
J(n,0)=0　n>0,
J(0,0)=1

δF(x,y)
δy		＝1-xy
xy(y+1)		F(x,y)-1
xy(y+1)		 より

　

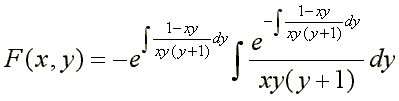
∫ 1-xy
xy(y+1)		dy
=∫(1
x		( 1
y		- 1
y+1		)- 1
y+1		)dy
=1
x		 ln y
y+1		 -ln(y+1) より

　

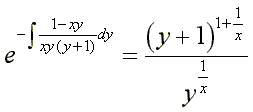
F(x,y)
= -y1/x
(y+1)1+1/x		∫ (y+1)1+1/x
y1/x*xy(y+1)		 dy
= -y1/x
x(y+1)1+1/x		∫ (y+1)1/x
y1+1/x		 dy

x= 1
z		 で置き換えると
F(x(z),y)= -z yz
(y+1)1+z		∫ (y+1)z
yz+1		 dy になります。

∫(y+1)z
yz+1		 dy
=-(y+1)z
zyz		+∫(y+1)z-1
yz		 dy
=- ∞

i=0		 (y+1)z-i
(z-i)yz-i		 +C(x)より
F(x,y)= ∞

r=0		 yr
(1-rx)(1+y)r+1		-y1/x C(x)
x(y+1)1+1/x

J(n,k)の初値より C(x)=0がわかります。

F(x,y)
= ∞

r=0		yr
(1-rx)(1+y)r+1
= ∞

i=0		 ∞

r=0		 (-1)i i+rCi yi
1-rx
= ∞

i=0		 ∞

k=i		 (-1)i kCi yk
1-(k-i)x

　J(n,k)
=F(x,y)の xn ykの係数
= ∞

i=0		 (-1)i kCi (k-i)n
= k

i=0		 (-1)i kCi (k-i)n

別のアプローチでやります。
Y.M.Ojisanさんの計算結果から
J(n,k)= k

i=0		 (-1)ikCi (k-i)n と予想できます。

ｋJ(n-1,k-1)+k J(n-1,k)
=k k-1

i=0		 (-1)ik-1Ci (k-1-i)n-1+ k k

i=0		 (-1)ikCi (k-i)n-1
= k-1

i=0		 (-1)i(i+1)kCi+1 (k-1-i)n-1+ k k

i=0		 (-1)ikCi (k-i)n-1
= k

i=1		 (-1)i-1(i)kCi (k-i)n-1+ k k

i=0		 (-1)ikCi (k-i)n-1
= k

i=1		 (-1)i(k-i)kCi (k-i)n-1
= k

i=1		 (-1)ikCi (k-i)n
= J(n,k)

さらに、
J(n,0)= 0

i=0		 (-1)i0Ci (0-i)n=0n　= 1 n=0,
　= 0 n>0.

J(0,k)= k

i=0		 (-1)ikCi (k-i)0=(1-1)k=0 k>0.

上記の帰納法より
J(n,k)は k

i=0		 (-1)ikCi (k-i)n であることがわかります。

P(n)
= n

k=1		J(n,k)
= n

k=1		 k

i=0		 (-1)ikCi (k-i)n
= n

k=1		 k

j=0		 (-1)jn-jCk-j (n-k)n

この式に至るもっときれいな説明があるでしょう。
とりあえず、答えは上記の式になります。

◆宮城県　アンパンマン さんからの解答。

J(n,k)の求め方。

ゴールする人がkグループある(0人のグループもありえるとします）とすると
ゴールする順番は kn 通りあります。

Eiはグループiが0人いるイベントです。

N(Ei) ＝イベントEiになる順番の数です。 ＝(k-1)n 通りです。

N(E1∪E2∪...∪Ek)
=
1≦i≦k		N(Ei)-
1≦i_1<i_2≦k		N(Ei_1∩Ei_2)+
1≦i_1<i_2<i_3≦k
 N(Ei_1∩Ei_2∩Ei_3)+・・

N(Ei_1∩Ei_2∩...∩Ei_r)
=n人をk-rのグループに分ける
=(k-r)n

N(E1∪E2∪...∪Ek)
= k

i=1		 (-1)i-1 kCi (k-i)n

J(n,k)
=N((E1∪E2∪...∪Ek)')
=kn-N(E1∪E2∪...∪Ek)
= k

i=0		 (-1)i kCi (k-i)n

◆出題者のFootmark さんからの解答。

アンパンマンさんが既に一般解を導き出していますが、私なりの解法です。

母関数(指数型母関数)を用いての解法です。

数列(ａ0,ａ1,ａ2,…,ａN,…)に対して、次の関数Ｇ(x)がこの数列の指数型母関数です。

Ｇ(x) ＝ａ0x0
0！		+ａ1 x1
1！		+ａ2x2
2！		+…+ａNxN
N！		 +…

ここでxN
N！		 は形式的な数で、
それ自身の値には何ら意味はなく、各項の係数のみに意味があります。

組合せの場合とは違い、順列そのものを母関数で表現するのは、どうしても無理があります。
と言うのは、順列では構成要素が同一でも順序が違えば別なものなので、可換である通常の代数では、これを表現することは不可能だからです。
そこで、順列そのものではなく、順列の数のみを指数型計数子として表現します。

Ｎ人が順番の違うｉ個のグループに分かれてゴールしたものとし、各グループについて考えてみます。
グループ内はＮ人以下なら何人でも許され、その内での並び方は問題としないので、指数型計数子は
x0
0！		+ x1
1！		+x2
2！		+x3
3！		 + … ＝ ex

ところが、グループ内には少なくとも１人はいる筈ですから、指数型計数子は
x1
1！		+x2
2！		+x3
3！		 + … ＝ ex-1

それ故、ｉ個のグループでは指数型計数子は以下のようになります。

　 (ex-1)i
＝ i

j=0		iＣj (ex) i-j (-1)j
＝ i

j=0		iＣj (-1)j e(i-j)x
＝ i

j=0		 {iＣj (-1)j ∞

N=0		 1
N！		 (i-j)N xN}
＝ ∞

N=0		 { xN
N！		 i

j=0		iＣj (-1)j (i-j)N }

Ｎ人が順番の違うｉ個のグループに分かれてゴールする方法の数は、上の式の
xN
N！		 の係数なので i

j=0		iＣj(-1)j(i-j)N

この中で、ｊ＝ｉ の時は、iＣj(-1)j(i-j)N ＝ 0 となるため
i-1

j=0		iＣj(-1)j(i-j)N

ところで、グループの数(ｉ)は、１個からＮ個まであり得るので
N

i=1		 i-1

j=0		iＣj(-1)j(i-j)N

これが求めるＮ人の同順を許す並び方の数です。

なお、各グループでの人数はＮ人以下なので、各グループの指数型計数子は本来ならば

x1
1！		+x2
2！		+x3
3！		 + …+xN
N！

とすべきですが、無限次数までの和としても、全グループでの
xN
N！		の項の係数の計算結果は変わりません。

さらに、上の式を展開させてから再度 kN(kは 1≦k≦N の整数) で整理すると
N

i=1		 N-i

j=0		(-1)ji+jＣj iN

この式が「パスカルの三角形による解法」の元になった式です。

【余談】

この「同順を許す並び方」の一般解には注意が必要です。
と言うのは、Ｎ人が１人ずつＮ個のグループに分かれる場合も保証されないと成立しないからです。
たとえば次のようなケースでは、すべての正の整数Ｎにおいて成立する訳ではありません。

同じ年齢のＮ人の人を誕生日順に並べる場合は、
Ｎ＞過去１年間の日数 では成立しません。

　『同順を許す並び方の数は？』へ

　数学の部屋へもどる