◆山梨県 Footmark さんからの解答。
便宜上、次のように定義する。
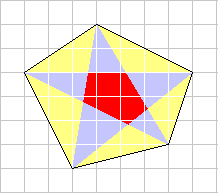
各星先三角形内において格子点が確認されているのは、内五角形から最長点にあたる外五角形の5頂点のみである。
そこで、各星先三角形内に内五角形からより近距離の格子点があれば、外五角形の頂点をそちらに置き換えるものとする。
すると、新たな5つの格子点でできる外五角形も内五角形も、元の範囲の内部に縮小したやはり凸五角形となる。
それ故、縮小後の内五角形内に格子点が存在すれば、縮小前の内五角形内にも格子点が存在することになる。
そこで、この置き換え操作を可能な限り繰り返したものとする。
よって、以後は
各星先三角形内に外五角形の頂点以外の格子点は存在しない。・・(1)
何故なら、外五角形の頂点以外の格子点が星先三角形内にあるのなら、その格子点を外五角形の頂点にできる筈である。
また、平面上の格子点を(x,y)座標の偶奇で表すと
(偶,偶)か(奇,奇)か(偶,奇)か(奇,偶)の4つの偶奇座標しかあり得ない。
それ故、格子点が5つあれば、少なくともその内の2つの偶奇座標は同一にならざるを得ない。
同一偶奇座標の2つの格子点では、偶数,奇数が一致するため各座標の和は偶数となり、
中点の各(x,y)座標は整数となる。
よって、同一偶奇座標の2つの格子点の中点は格子点にある。
このことより、平面上の5つの格子点は、その内の2つの中点が格子点にあるものが少なくとも1つはある。
ところで、3つの格子点が同一直線上にあることも許すと、確認された中点格子点が元々与えられた格子点である場合もある。
しかし、凸五角形を形成するとなるといずれの3つも同一直線上にないので、確認できる格子点の数は少なくとも1つは必ず増える。
それ故、5つの格子点が凸五角形を形成する限り、少なくとも1つは新しい格子点が確認できる。・・(2)
また、確認済みの格子点が外五角形の5頂点のみなら、新たに確認可能な中点格子点の存在位置は次のいずれかである。
前の図より明らかのように、対角線上の点は必ず星先三角形か内五角形のいずれかに含まれる。
ところが格子点となると、(1)より既に星先三角形内には外五角形の頂点以外の格子点は存在しない筈である。
また、中点は対角線の両端である外五角形の頂点にはあり得ない。
よって、格子点は内五角形内に存在することになる。
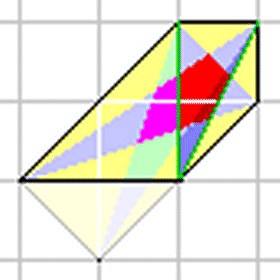
【外五角形の辺の中点に格子点が確認できる場合】
その辺の両端である外五角形の2頂点の内の任意の1頂点を中点格子点に置き換えるものとする。

すると、新たな5つの格子点でできる外五角形は元の範囲の内部に縮小した凸五角形となる。
内五角形も凸五角形となるが、元の範囲の一部(図の紫部分)が除かれ新たな部分(図の濃赤部分)が追加される。
ところが、追加部分は必ず元の星先三角形内の外五角形の頂点以外の一部である。
(1)より、星先三角形内には、外五角形の頂点以外の格子点は存在しない筈である。
それ故、この置き換えをしても内五角形内に新たな格子点が加えられることはない。
(当然のことだが、内五角形内の格子点の存在証明には全く影響を与えない)
また、(2)より外五角形の辺の中点に格子点が確認できる限り、いくらでもこの置き換えは可能である。
ところが、外五角形内の格子点の数は有限個なので、際限なく外五角形が縮小されはしない。
必ずいずれは外五角形の対角線の中点に格子点を確認する。
以上より、縮小され尽くした外五角形において、その内五角形内に格子点は必ず存在する。
よって、与えられた5つの格子点による元の内五角形内にも格子点は必ず存在する。
証明終わり。
【P・S】
更新履歴によると、2000年3月8日の出題で既に1年8ヶ月以上も経過していました。
ところが、解答はまったく無く未解決、さらに驚いたことは出題者は当時中学1年生でした。
証明では「幾何的な発見」から「部分にあれば全体にある」,「鳩の巣箱の原理」など、いくつかの小技を用いざるを得ませんでした。
それらを要求するこの証明問題はそれ故とても面白く非常に名問題だと思います。
◆大阪府 yosit さんからの解答。
Footmark さんの解答を整理しました.
凸五角形Pの頂点AをP上の点A’におきかえて凸五角形P’をつくる.
このときP’の内五角形はPの星形にふくまれる.
特にA’がPの星形上にあるならば,P’の内五角形はPの内五角形にふくまれる.
このことから,格子凸五角形で内五角形上に格子点のないものが存在するならば,その中に格子凸五角形で星形に格子点のないものが存在し,さらにその中に格子凸五角形で頂点以外の格子点をもたないものが存在しなければならない.
一方,格子点の各座標の偶奇は4通りなので,5つの格子点の内の2つは偶奇が一致し,その中点が格子点になる.
したがって格子凸五角形は頂点以外の格子点をもつ.
以上により,格子凸五角形の内五角形は格子点をもつ.
◆東京都 建築家 さんからの解答。
ヒントを使わない方法です。
図と用語はFootmarkさんのを借りることにします。
14行目までの説明にあるように
「各星先三角形内に外五角形の頂点以外の格子点は存在しない。 (1)」
とすることが出来ます。
次に5頂点のX座標Y座標を(Xi,Yi) (i=1,2,3,4,5)とします。
Xi,Yiの中央値をMed(Xi),Med(Yi)とすると
点(Med(Xi),Med(Yi))は☆型の内側に存在します。
ところが(1)より星先三角形内には格子点が存在しないことから、この点は内五角形に含まれることになります。■
◆山梨県 Footmark さんからのコメント。
建築家さんの解答に対するコメントです。
点(Med(Xi),Med(Yi))が外五角形の頂点自身になることもありますから、
内五角形内に格子点が存在する証明にはなりませんね。
例えば、外五角形の5頂点が (2,2),(3,0),(2,0),(0,2),(0,3) なら、
各星先三角形内に外五角形の頂点以外の格子点は存在しませんが、
点(Med(Xi),Med(Yi))は、外五角形の1頂点(2,2)です。
◆東京都 建築家 さんからの解答。
【仮定】「内五角形の内部,或いは周上に格子点が含まれない格子点凸五角形が存在する。」・・・(1)
として矛盾を導く。
《(1)を満たす五角形Aについて》
頂点を除いて星先三角形内に格子点が存在すれば,その点とAの頂点から格子点凸五角形Bを作ることが出来る。
その内五角形B'は内五角形A'に完全に含まれるのでBも(1)を満たす。
有限の操作により以下の図形を(Aの内側に)見出せる。
「☆形の内部,或いは頂点を除く周上に格子点が含まれない格子点凸五角形が存在する。」・・・(2)
《(2)を満たす五角形Cについて》
Cの頂点を除く内部に格子点が存在した場合,その点とCの頂点から(1)を満たす格子点凸五角形Dを作ることが出来る。
というのも内五角形D'はCの☆形の内側であるので。
つまり(1)を満たす五角形の頂点を除く内部に格子点が存在すれば,その内側にも(1)を満たす五角形を見出すことができる。
よって,「頂点以外には格子点を含まない格子点凸五角形が存在する。」・・・(3)
(ところが(3)を満たす格子点五角形の面積はピックの定理により 0+5/2-1=1.5)
しかしそのような格子点凸五角形は存在しないので矛盾であり【仮定】は誤っている。
よって,「いかなる格子点凸五角形においても内五角形内或いは周上に格子点が含まれる。」■
背理法の方が証明はしやすいかもですね。
一応ヒント用いずですがもっと簡単な証明がありそうな気がします・・
◆東京都 建築家 さんからの解答。
五角形のそれぞれの頂点を通り、原点と点(n,m)を通る直線に平行な5つの直線のうち
中心を通るものをCL(n,m)とする。
(n,m∈Z、直線は重複してもかまわない)
この時、CL(n,1)とCL(1,0)、CL(1,m)とCL(0,1)の交点の集合は全て格子点でありこの集合をGとする。
ところでCLは必ず内五角形を通り、2つのCLの交点は内五角形内にあるか外五角形の頂点である。
Gの要素のうち内五角形に含まれるものがあれば題意をみたす。
もしそうでなければGの全ての要素が外五角形の頂点でなければならないがそれらは全て一致し|G|=1となる。
しかし一つの頂点を通る直線が常に中心線となることはない。
よって内五角形に格子点は含まれる。■
帰納的な方法を使わず最初の方針でリベンジしてみました。
丁寧に証明しようとするとあまりエレガントな解法ではないかもです。
◆東京都 建築家 さんからの解答。
格子点の集合を
ようやく最初の方針でリベンジできましたが結構難しい解法になってしまいました。
L = {(n,m) |n,m∈Z(整数) }
M = {
L' = {☆形に含まれる格子点}⊂L
とする.
(この時L = {nP+mQ|n,m∈N,∃
五角形のそれぞれの頂点を通りベクトルP∈Lに平行な5つの直線のうち中心を通るものをCL(P)とする.
G={CL(P)∩CL(Q)|
G'⊆G⊆L'.
適当な対角線X=n(P+Q)∈L (n∈N,|X|>|P|,|Q|,
n=1 の時 CL(P)∩CL(Q) ∈ G'≠φ.
n≠1 の時 X上の格子点 ∈ G'≠φ.
今,星先三角形内に格子点が存在しないとすると
G'≠φ⊆L'の要素は題意を満たす.■
格子点ベクトルの性質を使ってみました。
できれば帰納的な要素(最後の一行)はなくしたかったのですが・・・。