仧帬夑導丂ippei 偝傫偐傜偺夝摎丅
亂栤戣俆亃
戞侾徾尷偍傛傃幉忋偵揰傪師偺傛偆偵偲傞丅
a(0,a),B(0,0),C(c,0),D(c,d),E(e,d),F(e,a)
俁捈慄偺曽掱幃偼
| y= | d-a c |
x+a丂丂丂(1) |
| y= | d e |
x丂丂丂(2) |
| y= | -a c-e |
(x-c)丂丂丂(3) |
(1)(2) 偺楢棫偟偨夝傕 (2)(3) 偺夝傕偲傕偵
| x= | ace cd-de+ae |
丆y= | acd cd-de+ae |
偲側傞偐傜丄俁捈慄偼侾揰偱岎傢傞丅
仧愮梩導丂側偺偼側巕 偝傫偐傜偺夝摎丅
亂栤戣俁亃

仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俁亃
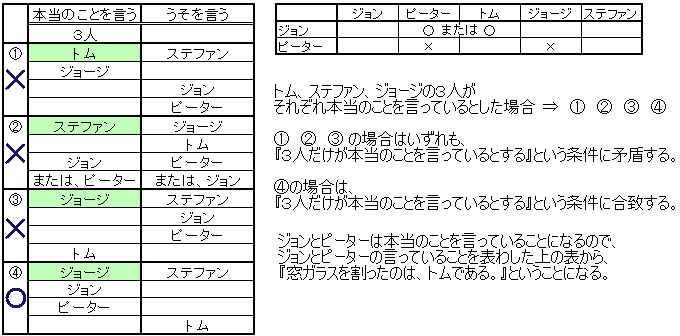
亂摎偊亃丂憢僈儔僗傪妱偭偨偺偼僩儉丅
杮摉偺偙偲傪尵偭偰偄傞偺偑丄僕儑儞偲僺乕僞乕偲偐僕儑乕僕丅
偆偦傪偮偄偰偄傞偺偑丄僩儉偲僗僥僼傽儞丅
俆恖傪侾恖偢偮弴偵斊恖偲壖掕偡傞偲丄僩儉埲奜偺偲偒偼乽偆偦乿偑俁恖偵側傞偺偱敾柧偟傑偡丅
[ P丒S ]
僩儉丗乽僕儑儞傕僺乕僞乕傕偆偦傪偮偄偰偄傑偡丅乿
僗僥僼傽儞丗乽偄偄偊丄僕儑儞偲僺乕僞乕偺偆偪丄堦恖偩偗偆偦傪偮偄偰偄傑偡丅乿
僩儉偲僗僥僼傽儞偺庡挘偼攚斀揑偱俀恖偲傕乽杮摉乿偼偁傝摼側偄丅
屘偵丄偳偪傜偐1恖偑乽杮摉乿偱丄偳偪傜偐侾恖偑乽偆偦乿丅
偲偡傞偲丄傒偛偲棊偲偟寠偵棊偪偰偟傑偄傑偡丅
俀恖偲傕乽杮摉乿偺斲掕偼丄乽杮摉乿偲乽偆偦乿偩偗偱側偔丄俀恖偲傕乽偆偦乿傕偁傝傑偡丅
杮栤偺応崌偼僩儉偲僗僥僼傽儞偺庡挘偼俀恖偲傕乽偆偦乿偱偡丅
偮傑傝丄僕儑儞傕僺乕僞乕傕杮摉偺偙偲傪尵偭偰偄傞応崌偵偦偆側傝傑偡丅
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣係亃(侾)
埲屻丄{丂 }偺婰崋偼寁嶼忋暣傜傢偟偄偺偱亂丂 亃偵抲偒姺偊偰昞尰偡傞丅
俁埲忋偺偡傋偰偺惍悢値偵偍偄偰丄
| 倎亖亇 | 値亇 俀 |
偼忦審傪枮偨偡丅 |
壗屘側傜丄俁埲忋偺惍悢値側傜丄![]() 偼柧傜偐偵柍棟悢丅
偼柧傜偐偵柍棟悢丅
| 亪丂侽亙亂亇 | 値亇 俀 |
亃亙侾 |
| 傑偨丄亇 | 値亄 俀 |
偲 亇 | 値亅 俀 |
偲偼丄屳偄偵媡悢摨巑丅 |
亪
| 丂亂倎亄 | 侾 倎 | 亃 |
| 亖亂亇( | 値亄 俀 |
亄 | 値亅 俀 |
)亃 |
| 亖亂亇値亃 |
| 亖侽 |
埲忋傛傝丄
| 丂亂倎亃亄亂 | 侾 倎 | 亃亖侾 |
値偺彫偝偄弴偵椺傪帵偡丅
亂栤戣係亃(俀)丂[徹柧]
柧傜偐偵丄倎亗侽丅
| 倎亄 | 侾 倎 | 亖亇値丅(偨偩偟丄値偼惓惍悢丅) |
| 亪丂倎亖亇 | 値亇 俀 |
仠値亖侾側傜丄倎偼幚悢偲偼側傜側偄偺偱忦審偵斀偡傞丅
仠値亖俀側傜丄倎亖亇侾丅
| 亪丂亂倎亃亄亂 | 侾 倎 | 亃亖侽亗侾 |
忦審傪枮偨偝側偄丅
値亞俁側傜丄柧傜偐偵(侾)偱帵偟偨傛偆偵丄
| 倎亖亇 | 値亇 俀 |
偼忦審傪枮偨偡丅 |
埲忋傛傝丄
| 倎亖亇 | 値亇 俀 |
(偨偩偟丄値偼俁埲忋偺惍悢) |
| 亇 | 値亇 俀 |
偼柧傜偐偵柍棟悢丅 |
傛偭偰丄倎偼柍棟悢偱偁傞丅
徹柧廔傢傝丅
[ P丒S ]
幚悢 x 偺彫悢晹暘傪 亂x亃偲彂偔偙偲偵偟傑偡丅
側偺偐丄
亂x亃= x - [x] 偱偡丅( [丂] 偼僈僂僗婰崋)
側偺偐丄崱堦偼偭偒傝偟傑偣傫丅
慜幰偱偁傞側傜丄亂亅侾丏俀亃亖亅侽丏俀
屻幰偱偁傞側傜丄亂亅侾丏俀亃亖侽丏俉
乮屻幰側傜丄忢偵亂倶亃亞侽丅乯
屻幰偺堄枴側傜丄
幚悢 x 偵偍偄偰丄亂x亃= x - [x] 偲偟傑偡丅( [丂] 偼僈僂僗婰崋)
偩偗偺曽偑傛偐偭偨偺偱偼乨丅
夝摎偼屻幰偱偡偑丄慜幰側傜倎亜侽偱側偄偲忦審傪枮偨偝側偄偺偼柧傜偐丅
| 傛偭偰丄倎亖 | 値亇 俀 |
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣俀亃
乮侾乯佹
| 9 11 | = | 1 A | + | 1 B | + | 1 C |
ABC傪偐偗傞偲丄
9ABC=11(AB+BC+CA)丂偱偁傝丄A,B,C偺壗傟偐偼侾侾偺攞悢丅
| 傑偨丄 | 9 11 | 乛3 = | 3 11 | 亜 | 1 11 |
偱偁傞偐傜丄A偼侾侾枹枮丅 |
| A=2偲偟偰傕丄( | 9 11 | - | 1 2 | )乛2 = | 7 44 | 亜 | 1 11 |
| 傛偭偰丂俠亖 | 1 11m | 丄m:帺慠悢偱側偗傟偽側傜偢丄 |
| C亝 | 1 11 |
| 偙傟傛傝丂 | 1 A | + | 1 B | 亞 | 8 11 |
| 傛偭偰丂 | 1 A | 亞 | 4 11 | 亜 | 1 3 |
偙偺傛偆側A偼俀偺傒丅A=2傪戙擖偡傞偲丄
| ( | 9 11 | - | 1 2 | )= | 7 22 | 亜 | 1 B | 亞 | 8 11 | - | 1 2 | = | 5 22 | 傛傝 |
B=4偺傒壜擻惈偁傝丅
| 1 C | = | 9 11 | - | 1 2 | - | 1 4 | = | 3 44 |
傛偭偰懚嵼偟側偄丅
乮俀乯柍偄丅
| X Y | = | 1 A | + | 1 B | + | 1 C |
| X Y | 伕( | 41 42 | ,1)偱偁傞偲偡傞偲傑偢丄A=2偱偁傞丅 |
佹傕偟A亞俁偲偡傞偲A=B=C=3偺帪
| 1 A | + | 1 B | + | 1 C | =1偱斖埻奜偱偁傞丅 |
師偵彫偝偄悢偼丂A=B=3 C=4偱偁偭偰丄
| 1 A | + | 1 B | + | 1 C | = | 11 12 | 亙 | 41 42 |
| 偦偺傎偐偺慻傒崌傢偣偼偝傜偵 | 41 42 | 傛傝彫偝偄丅 |
傛偭偰丄A=2偱偁傞丅
| 廬偭偰栤戣偼 | X Y | = | 1 B | + | 1 C |
| 2亝B亝C丄B丆C丗惍悢丄 | X Y | 伕( | 10 21 | , | 1 2 | ) |
B=2偱偼婛偵斖埻奜偱偁傞偐傜幚嵺偵偼俁亝B亝C偱偁傞丅
| 堦曽B=C=5偱偼 | 1 5 | + | 1 5 | = | 2 5 | 亙 | 10 21 |
乮B=3乯偺応崌
| 1 C |
伕( | 41 42 | - | 1 2 | - | 1 3 |
,1- | 1 2 | - | 1 3 | ) = ( | 1 7 | , | 1 6 | ) |
乮B=4乯偺応崌
| 1 C |
伕( | 41 42 | - | 1 2 | - | 1 4 |
,1- | 1 2 | - | 1 4 | ) = ( | 19 84 | , | 1 4 | ) |
| 84 19 |
亙俆偩偐傜偦偺條側惍悢C亞係偼柍偄丅 |
亂姶憐亃
偆傑偔峫偊傜傟偨栤戣偱偡偹丅
亂栤戣俇亃
壓恾偺傛偆偵係柺懱偼壜擻偱偁傞丅
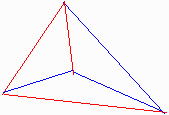
柺偑慡晹俁妏宍偱偁傞擟堄偺扨堦椞堟偺懡柺懱偺廤崌傪儼偲偡傞丅
S伕儼偼丄壗傟偐偺曈傪挿偝侽偵弅傔傞偙偲偵傛傝丄
捀揰偺悢偑侾丄柺偺悢偑俀丄曈偺悢偑俁彮側偄S乫伕儼偵曄宍偑壜擻偱偁傞丅
埲屻偙傟傪孞傝曉偡偙偲偵傛傝S偼揾傝暘偗壜擻側係柺懱伕儼傑偱曄宍壜擻偱偁傞丅
壓恾
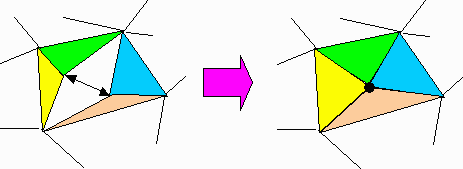
廬偭偰丄師偺婯懃偱曈偵怓傪偮偗側偑傜丄媡偺庤弴傪偨偳偭偰丄係柺懱偐傜尦偺S偵偨偳傝拝偗偽丄姰惉偟偨揾傝暘偗偼戣堄傪枮偨偡揾傝暘偗偱偁傞丅
乮侾乯媡弴偵偍偄偰尦偵栠偡俀柺乮俁妏宍乯偺嫟捠曈乮挿偝傪傕偳偡曈乯傪彍偔曈偺怓偼丄廳側偭偰偄偨偲偒偺曈偺怓傪宲彸偡傞丅
壓恾嶲徠丅
乮俀乯嫟捠偺曈偺怓偼丄乮侾乯偱宲彸偟偨曈偺怓偲堎側傞怓傪揾傞丅宲彸偟偨怓偑俀怓偁傞偲偒偼偳偪傜偱傕椙偄
乮壓恾偱偼愒乯丅
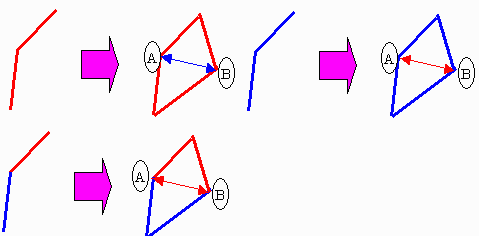
埲忋偺傛偆偵揾傝暘偗傞偲丄忋恾偺傛偆偵暘棧偝傟偨揰A,B娫偵偼愒偺傒宱楬偲惵偺傒宱楬偑昁偢懚嵼偟丄幚幙侾偮偺揰偲摨偠偱偁傞丅
傛偭偰丄奐偔慜偺忬懺偵偍偄偰丄戣堄傪枮偨偡俀宱楬偑懚嵼偟偰偄傟偽丄奐偄偨屻傕擟堄偺揰娫偱惵宱楬丄愒宱楬偑懚嵼偡傞丅
亂俹俽亃
撌懱傛傝扨楢寢懱偺傎偆偑徹柧偟傗偡偄偺偱斖埻傪奼戝偟傑偟偨丅
亂栤戣俈亃
俀侽埲壓偺慺悢偼丂2,3,5,7,11,13,17,19偺俉屄偱偁傞丅
廬偭偰丄侾侽屄偺帺慠悢偼丂
N=俀俙俁俛俆俠俈俢侾侾俤侾俁俥侾俈俧侾俋俫偱昞偝傟傞丅
偙偙偱俙乣俫偼旕晧惍悢偱偁傞偑丄愊偑暯曽悢偱偁傞偐偳偆偐偩偗偑栤戣側偺偱丄嬼婏惈偩偗峫偊傟偽傛偔丄俙乣俫偼侽偐侾偵尷掕偟偰傛偄丅
傑偨丄奺俶傪慖傇偐慖偽側偄偐傕侽偐侾傪偐偗傞偙偲偵懳墳偝偣偆傞偺偱丄
俶傪[A,B,C,D,E,F,G,H]偲偄偆儀僋僩儖偱昞傢偣偽丄俀傪朄偲偡傞俉師尦偺桳尷懱乮奼戝僈儘傾懱乯偵偍偗傞侾侽屄偺儀僋僩儖偼撈棫偐偲偄偆栤戣偵摍壙偱偁傞丅
偙傟偼慄宍戙悢偺婎杮偱偁傝撈棫偵偼偱偒側偄丅
懄偪丄侾侽屄傛傝彮側偄俋屄偁傟偽偦偺偆偪偐傜婔偮偐慖傜傫偱愊傪暯曽悢偵偱偒傞丅
嬶懱揑偵偼奺俶傪峴偲偟偰暲傋偨俋亊俉偺峴楍傪嶌惉偟丄峴娫偺墘嶼偵傛傞媡峴楍偺媮傔曽偺曽朄偱忋嶰妏峴楍壔偟偰備偗偽丄彮側偔偲傕俋峴栚偼侽儀僋僩儖偵偱偒傞丅
偦偺偲偒偺墘嶼憖嶌偺崌寁抣乮俀傪朄偲偡傞偺偱侽偐侾乯偱奺儀奺俶偺嵦斲傪寛傔傟偽傛偄丅
亂俹俽亃
俋屄偱傛偄偺偱偼丠
仧恄撧愳導丂僋儔僥僗 偝傫偐傜偺夝摎丅
亂栤戣侾亃
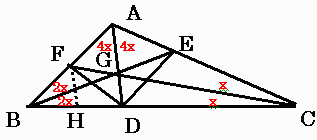
佢BAC=俉x丄佢ABC=係倶丄佢BCA=俀倶偲偟丄
佢BAC,佢ABC,佢BCA偲懳曈偲偺岎揰傪偦傟偧傟丄D,E,F偲偟丄撪怱傪G偲偡傞丅
偙偺偲偒侾係倶亖侾俉侽搙偱偁傞丅
傑偨F傪捠傝AD偵暯峴側捈慄傪堷偒BC偲偺岎揰傪H偲偡傞丅
嚈HFC偲嚈AFC偵偍偄偰
佢HFC亖佢DGC=佢GAC+佢GCA=俆x
佢CFA=佢FBC+佢FCB=俆x傛傝丄
佢HFC=佢CFA
佢FCH=佢FCA=倶
FC嫟捠傛傝
仮HFC佭仮AFC乮擇曈偲偦偺娫偺妏憡摍乯
傛偭偰丄FH=FA偱偁傞丅
佢HBF=係倶丄佢HFB=佢DAB=係x傛傝
佢HBF=佢HFB偲側傞偐傜丄仮HBF偼擇摍曈嶰妏宍偱偁傞丅
摨條偵仮AFG(椉掙妏5x),仮GAE(椉掙妏4x)傕擇摍曈嶰妏宍偱偁傞丅
偙傟傛傝丄FA=GA=GE偲側傞丅
偮傑傝仮HBF偲仮GAE偼崌摨側擇摍曈嶰妏宍偱偁傞丅
傛偭偰丄FB=EA偱偁傞丅
仮DFB偲仮DEA偵偍偄偰丄
FB=EA
仮DAB偼擇摍曈嶰妏宍偩偐傜BD=AD
佢FBD=佢EAD=係x傛傝丄
仮DFB佭仮DEA乮擇曈偲偦偺娫偺妏憡摍乯
寢嬊DF=DE偲側傝仮DEF偼擇摍曈嶰妏宍偲側傞丅
亂栤戣俉亃
f(x)=ax2+bx+c,g(x)=cx2+bx+a偲偡傞丅
|x|亝1偱|g(x)|亝俀偱偁傞偨傔偵偼
|x|亝1偱|f(x)|亝侾偩偐傜
|g(x)亅f(x)|亝俁
仺
|c亅a||x2亅侾|亝俁
仺
|c亅a|亝俁
偱偁傞偙偲傪帵偣偽廫暘偱偁傞丅
乮佹|x|亝侾偱|x2亅侾|亝侾乯
|x|亝侾偱|f(x)|亝侾傛傝丄
|f(-1)|亝侾
仺
亅侾亝a亅b+c亝侾丒丒丒(1)
|f(0)|亝侾
仺
亅侾亝們亝侾丒丒丒(2)
|f(1)|亝侾
仺
亅侾亝a+b+c亝侾丒丒丒(3)
(1)丄(2)傛傝
亅俀亝a亅b亝俀丒丒丒(4)
(2)丄(3)傛傝
亅俀亝a+b亝俀丒丒丒(5)
(4)丄(5)傛傝
亅俀亝a亝俀丒丒丒(6)
(2)丄(6)偐傜
|c亅a|亝俁偲側傞丅
傛偭偰戣堄偼帵偝傟偨丅
仧帬夑導丂ippei 偝傫偐傜偺夝摎丅
亂栤戣俈亃
Y.M.Ojisan 偝傫偺梡岅傪巊傢偝偣偰捀偒傑偡丅
俀侽埲壓偺慺悢偼丂2,3,5,7,11,13,17,19偺俉屄偱偁傞丅
廬偭偰丄侾侽屄偺帺慠悢偼
N=俀俙俁俛俆俠俈俢侾侾俤侾俁俥侾俈俧侾俋俫偱昞偝傟傞丅
偙偙偱俙乣俫偼旕晧惍悢偱偁傞偑丄愊偑暯曽悢偱偁傞偐偳偆偐偩偗偑栤戣側偺偱丄嬼婏惈偩偗峫偊傟偽傛偔丄 俙乣俫偼侽偐侾偵尷掕偟偰傛偄丅
偱偒傞悢偵拝栚偡傟偽丄28亖256捠傝偺婏嬼偺僷僞乕儞偑偁傞丅
1屄偐傜10屄傑偱偺悢偺愊偼
10C1+10C2+....+10C9+10C10亖210乕1亖1023偲偍傝
1023亐256亖3 梋傝255 側偺偱數偺憙尨棟傛傝彮側偔偲傕4偮偺僷僞乕儞偱婏嬼偑堦抳偡傞丅
偟偨偑偭偰偙偺側偐偺揔摉側2偮傕偺偺愊傪峫偊傞偲丄偱偒偨悢偼暯曽悢偱偁傞丅
亙ps亜
511亐256亖1偁傑傝255側偺偱 9屄偺帺慠悢偱傄偭偨傝丅
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俈亃
暯曽悢偱側偄帺慠悢側傜丄慡慺場悢偵偍偗傞奺巜悢偺撪偵丄婏悢偱偁傞巜悢偑彮側偔偲傕侾偮偼懚嵼偟側偗傟偽側傜側偄丅
偦偺忋丄偁傞値庬椶偺慺場悢偟偐嫋偝側偄偲偡傞偲丄
慡慺場悢偵偍偗傞奺巜悢偺嬼婏僷僞乕儞偼
柧傜偐偵(俀n亅侾)捠傝偁傞丅
乮埲屻丄乽慡慺場悢偵偍偗傞奺巜悢偺嬼婏僷僞乕儞乿偺偙偲傪丄娙扨偵乽僷僞乕儞乿偲屇傇傕偺偲偡傞丅乯
堦曽丄侾屄埲忋偺偳偺傛偆側愊傕暯曽悢偲偼側傜側偄値屄偺帺慠悢傪峫偊偰傒傞丅
乮値屄偺慺悢傪偦偺傑傑値屄偺帺慠悢偲偟偰傕偦偆偱偁傞傛偆偵丄柧傜偐偵偦偺傛偆側値屄偺帺慠悢偼懚嵼偡傞丅乯
値屄偺帺慠悢偵偍偄偰丄偦偺撪偺侾屄埲忋偺愊偼丄摨條偵(俀n亅侾)捠傝偁傞丅
傑偨丄(俀n亅侾)捠傝偺偳偺傛偆側愊傕暯曽悢偲偼側傜側偄偺偱丄
(俀n亅侾)捠傝偺愊偵摨堦僷僞乕儞偑懚嵼偟偰偼側傜側偄丅
寢嬊丄嫋偝傟傞(俀n亅侾)捠傝偺奺僷僞乕儞偵丄
(俀n亅侾)捠傝偺奺愊偑偦傟偧傟侾屄偢偮懚嵼偡傞偙偲偵側傞丅
帺慠悢傪侾屄憹傗偡偲愊偼(俀n+1亅侾)捠傝偵憹偊傞偑丄嫋偝傟傞僷僞乕儞偼晄曄偱偁傞丅
偡傞偲丄捛壛偟偨帺慠悢偑場悢偲側傞怴偨偵憹偊偨愊偵偲偭偰偼丄偳偺僷僞乕儞偵傕婛偵愭媞偺愊偑懚嵼偡傞丅
偦傟屘丄値庬椶偺慺場悢偵傛傞(値亄侾)屄偺帺慠悢偱偼丄偦偺撪偺偁傞侾屄埲忋偺愊偼昁偢暯曽悢偲側傞丅
偲偙傠偱丄俀侽埲壓偺慺悢偼丄俀,俁,俆,俈,侾侾,侾俁,侾俈,侾俋 偺俉屄丅
傛偭偰丄俉庬椶偺慺場悢偵傛傞俋屄偺帺慠悢偱偼丄俋屄偺撪偺偁傞侾屄埲忋偺愊偼昁偢暯曽悢偲側傞丅