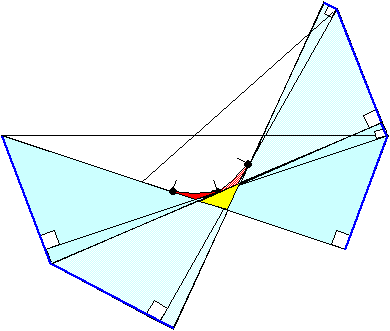
中央の包絡線で囲まれた3葉形の部分でも、2分割線は3回通過するだけである。
下図に3葉形の部分内部の詳細を示す。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
必ずしも正しくない。
正三角形は反例である。

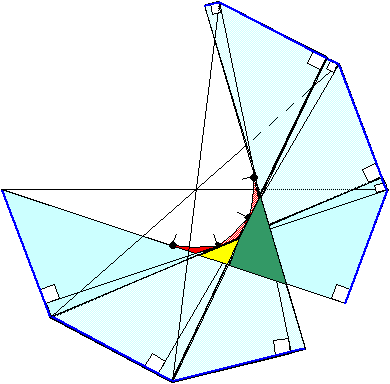
中央の包絡線で囲まれた3葉形の部分でも、2分割線は3回通過するだけである。
下図に3葉形の部分内部の詳細を示す。

【問題2】
1個 または 実数のオーダーで無限個
証明
明らかに円は1点である。
また問題1に示したように三角形では無限個であり存在する。
補題:
2分割直線の角度:θを定めると2分割直線は唯一定まる。
証明略
本題:
仮に2個以上有限個であるとする。
そのうちの異なる2点をA,Bとする。
A,Bを通る直線は唯一であるから、A,Bを両方通過する2分割直線は高々1本である。
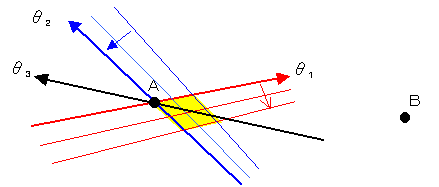
従って、残り2本へ移動するために、Aを通過している2分割直線はある角度θ1で一旦Aを離れ、再びAを通過する別の2分割直線に ある角度θ2で戻ってこなければならない。
また、残されたAを通過するもう一本の2分割直線の角度:θ3は、
θ2とθ1+πの間である。
Aの近傍での2分割直線のずれ方として、下図に示すType1とType2が考えられる。
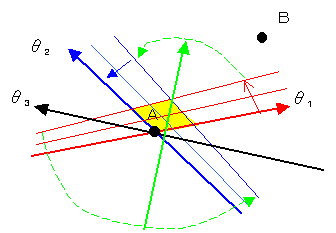
〇 Type1では、下図に示す黄色の2次元領域が点Aの近傍に存在し、ここではθ1とθ2に近い2本の2分割直線と角度θ3の2分割直線が通過しており、無限個のTの点が存在する。
〇 Type2では、θ1からθ2に移動する再に下図緑線で示すようにAの付近を通過しなければならず、同様に無限個のTの点が存在する。
よって、2個あればかならず無限個あるので、2個以上で有限個とはならない。
Type1
 |
 |
丁度3本と言う意図ではないと捉えました。
【考察問題】
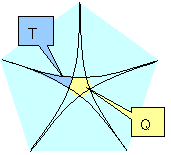
Sの異なる4本以上の線が交わる点の集合をQとする。
集合Qの要素の個数として考えられる数値を答えよ。
解答
0個、任意有限個、可算無限個、実数オーダーで無限個
(1)問題1に示したように0個の場合がある。
(2)円は1個の場合の例である。
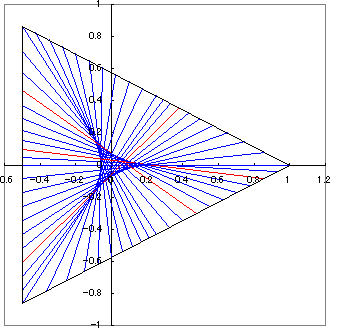
(3)正5角形では中央に包絡線で囲まれた2種の5葉の図形ができるが、内側の図形を2分割線は5回通る。従って、Qが実数オーダーで無限個存在する例である。
下図は誇張した図である。
(4)次のような部品を考える
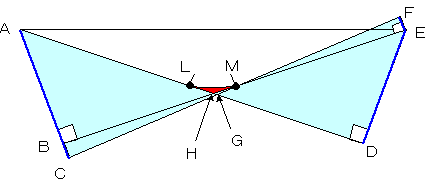
「定義」:AB=DE、AD=BE、BC=EF、AB//BC//EF
「性質」:AL=LD,BM=ME、CM=MF
ここで図形LMHはAD、BEが2分割直線であるとき、2分割直線の端点がA→Bに移動する間に2分割直線が掃引する領域で、2分割直線が2回通過する領域である。
一方、図形ABCGDEFMHLは境界を除き除き、端点がA→Cに移動する間に2分割直線が1回通過する領域である。
また点Mは端点がB→Cに移動する間に∞回2分割直線が通過する点であって、既にQの要素である。
また、2分割直線の包絡線という条件から前記の「性質」が導かれる。
この部品を実際はAB、BC長を図示よりかなり短くし、左右対称に積み重ねて行くことにより、任意個のQの点を持つ図形を作ることができる。
奇数個の場合は、FCのラインを左右対称の中央のラインとして始めればよい。
点Mが重なるので奇数個になる。
偶数個の場合は、ADのラインを左右対称の中央のラインとして始めればよい。
可算無限個の場合は、ABC長さの数列の無限和が収束するようにとればよい。
積み上げて行く場合下図(実際にはもっと薄い部品を使うので回転角度は小さい)に示すような、黄色、緑の領域がオーバーラップするが、図に示されるように、精々2回までであり、Tの要素となることはない。
さらに、左右対称に重ねることにより 図形LMHや積み上げでできた2回通過の領域には、鏡像側からもう一本の2分割直線が通過する可能性があるが、最大でもTの要素となるだけである。
従って、Qの要素となるのは点Mだけである。
最終的に得られる図形は『凸図形の面積、周の二等分』解答 の加算無限個のコメントの図とほぼ同じであり、下に示す完成前図(中央部は拡大誇張している)のようになる。
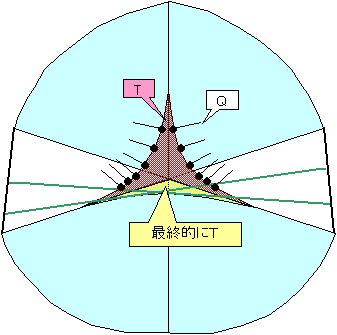
最後に残った部分の分割線を掃引すると、中央部に3葉形をしたTの要素の集合があって、その周上に有限個ないし可算無限個のQの要素が並んでいる図が得られる。
2段積み