晹昳俀乮偨偩偟恾拞値亖値乕侾乯傪侾枃丄揰俷偺夞傝偵抲偒丄倫抣偑慡偰堎側傞傛偆偵偡傟偽傛偄丅
枩堦丄晹昳俀偵傛傝偱偒傞摿庩側暘妱慄乮俀杮乯偺挿偝偲堦抳偟偨応崌偼彮偟偢傜偣偽傛偄丅
亂栤戣俁亃
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣侾亃
擟堄偺帺慠悢n偵懳偟丄n=L(T)偲側傞傛偆側T偼懚嵼偡傞丅
亙嶌惉椺亜
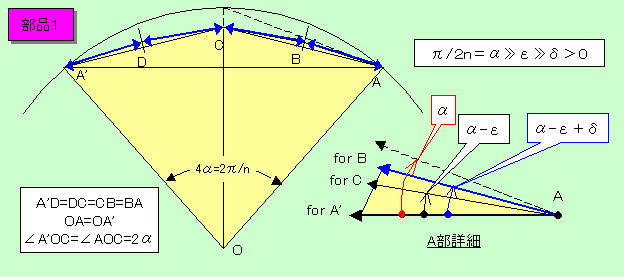
値亖侾丄俀偺応崌偼屻敿徹柧拞偺曗戣値亖侾丄俀嶲徠丅
値亞俁偺婏悢偺応崌偼壓恾偵帵偡晹昳侾傪値枃丄揰俷偺夞傝偵抲偗偽傛偄丅
値亞係偺嬼悢偺応崌偼壓恾偵帵偡晹昳侾乮偨偩偟恾拞値亖値乕侾乯傪値亅俀枃丄
晹昳俀乮偨偩偟恾拞値亖値乕侾乯傪侾枃丄揰俷偺夞傝偵抲偗偽傛偄丅
亂栤戣俀亃
L(T)杮偺慄暘偺挿偝偑慡偰堎側傞応崌偱傕丄忋偺柦戣偼惓偟偄偲尵偊傞丅
亙嶌惉椺亜
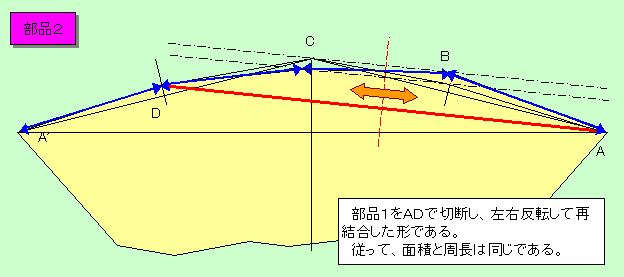
値亖侾丄俀偺応崌偼屻敿徹柧拞偺曗戣値亖侾丄俀嶲徠丅
尦乆挿偝偼堎側偭偰偄傞丅
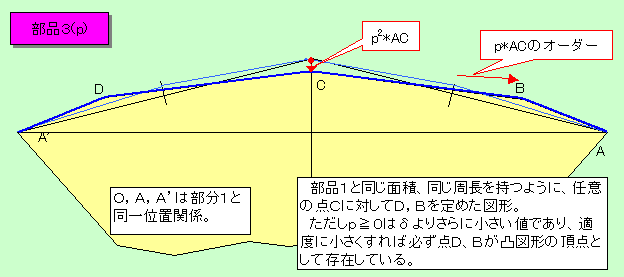
値亞俁偺婏悢偺応崌偼壓恾偵帵偡晹昳俁(p)傪値枃丄揰俷偺夞傝偵抲偒丄倫抣偑慡偰堎側傞傛偆偵偡傟偽傛偄丅
値亞係偺嬼悢偺応崌偼壓恾偵帵偡晹昳俁(p)乮偨偩偟恾拞値亖値乕侾乯傪値亅俀枃丄
晹昳俀乮偨偩偟恾拞値亖値乕侾乯傪侾枃丄揰俷偺夞傝偵抲偒丄倫抣偑慡偰堎側傞傛偆偵偡傟偽傛偄丅
枩堦丄晹昳俀偵傛傝偱偒傞摿庩側暘妱慄乮俀杮乯偺挿偝偲堦抳偟偨応崌偼彮偟偢傜偣偽傛偄丅



亂栤戣俁亃
L(T)杮偺慄暘偺挿偝偺嵟戝抣傪M丄嵟彫抣傪m偲偡傞偲偒丄
Mm亞S偼昁偢偟傕惉棫偟側偄丅
偨偩偟丄S偼恾宍T偺柺愊偱偁傞丅
亙斀椺亜
亙亙徹柧亜亜
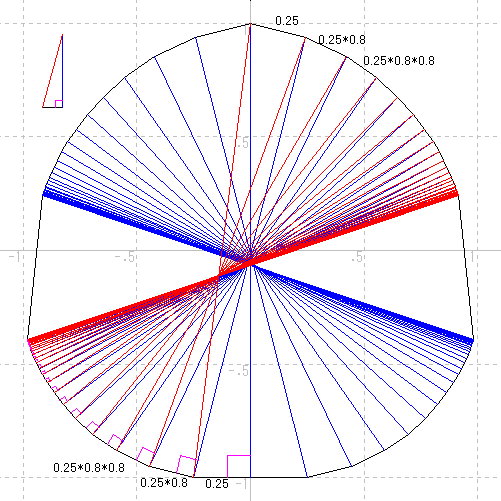
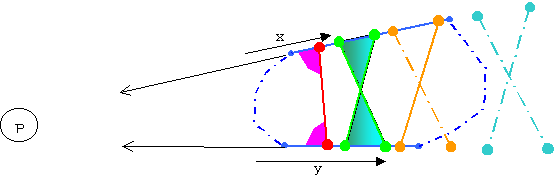
堦斒偺俿偺堎側傞暯峴側俀曈忋偵奺抂揰傪帩偮Bk偺悢偼侽偐侾偐亣偱偁傞丅
佹徣棯丂恾偩偗帵偡丅
亂曗戣俀亃
俿偺堎側傞乮暯峴偱側偄乯俀曈忋偵抂揰傪帩偮Bk偺悢偼侽偐侾偐俀杮偱偁傞丅
拲婰乯侾杮偺応崌偼丄俀杮偑廳側偭偨廳崻偺応崌偲堦曽偑斖埻奜偺応崌偑偁傞丅
侽杮偺応崌偼丄夝偑柍偄応崌偲慡偰偑斖埻奜偺応崌偑偁傞丅
佹丂俀曈偺墑挿偺岎揰傪俹偲偟丄俹偐傜抂揰傑偱傪偦傟偧傟倶丄倷偲偡傞丅
廃傪俀摍暘偡傞娭學偺忦審偼x亄y亖V丗掕悢偱昞傢偣傞丅
堦曽柺愊傪俀摍暘偡傞娭學偺忦審偼倶倷亖嚈丗掕悢偱昞傢偣傞丅
傛偭偰偙傟偼2師曽掱幃偱偁傝丄崻偼侽偐侾偐俀屄偱偁傞丅
偦偟偰曈偺懚嵼斖埻偵傛傝丄偙傟傜傛傝侾杮側偄偟俀杮偑寚偗傞応崌偑偁傞丅
亂曗戣俁亃
丂L(俿)偼桳尷屄偱偁傞丅
佹掕媊侾偲曗戣俀傛傝惉棫偡傞丅
亂曗戣係亃
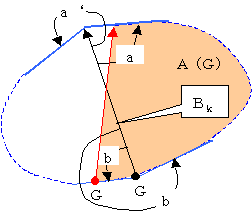
A(G)+A(G+U)=0
佹儲乮G乯亖亅儲乮G亄U乯偱偁傞偐傜丂A'(G+U)偼G偺嵍懁柺愊偱偁傞丅
傛偭偰A(G)亄A'(G)亖俀D偱偁傞丅丂
亂曗戣俆亃
L(T)亞侾
佹曗戣俁傛傝丂A(佄G)亗侽偱偁傞丅
廬偭偰A(佄G)亜侽偱偁傟偽曗戣係傛傝丂A(佄G+U)亙侽偱偁傝丄A乮G乯偺楢懕惈偐傜彮側偔偲傕堦売強A(G)亖侽偲偡傞G偑懚嵼偡傞丅
媡傕摨偠丅
亂曗戣俇亃
L(T)偼婏悢偺傎偆偑嶌傝傗偡偄丅
佹L(T)偼丂佄G亝G亙佄G亄U丂偵偍偗傞A(G倠)亖侽偲偡傞G倠乮夝乯偺悢偱偁傞丅
曗戣俆傛傝A(G)偑A(G)亖侽傪岎嵎偟偰娧捠偡傞応崌偼俴乮俿乯偼婏悢偱偁傞丅
廬偭偰丄俴乮俿乯偑嬼悢偵側傞偨傔偵偼A(佄G倠)亖侽偵偍偄偰A(G)偑俙亖侽偵偪傚偆偳愙偡傞乮廳崻乯偐丄倁帤宆偵愜傝曉偡昁梫偑偁傞丅
廬偭偰丄揔梡偵俿傪嶌傞偲戝掞俴乮俿乯偼婏悢偱偁傞丅
丂
亂曗戣俈亃
壓恾偺忬懺偵偍偄偰俙乮俧乯偑俛倠傪嫬偵倁帤宆偵曄壔偡傞偺偼丂
乷sin(倎)亜sin(倐)丂偐偮丂sin(倎')亜sin(倐')乸丂偐丂
乷sin(倎)亙sin(倐)丂偐偮丂sin(倎')亙sin(倐')乸丂偺応崌偱偁傞丅
佹俙乮俧k乯亖侽側偺偱丂
俙乮俧乯亖俙乮俧乯亅俙乮俧k乯亖乷[俧k][俧+倀]亊 [俧k亄倀]乸[俧]乛俀偱偁傞丅
|俛k|=1偵婯奿壔偟丄乥[Gk][G]乥亖乥[俧亄倀] [俧k亄倀]乥亖倶丂偲偟偰寁嶼偡傞偲丄
丂俙乮俧乮倶乯乯亖倶*乮倶*sin(a+b)+sin(倐)-sin(倎)乯/2 偱偁傞丂
廬偭偰倶亖亄侽丂偵偍偄偰丄俙乮俧乮倶乯乯偺孹偒偼丂sin(倐)-sin(倎)乯/2偱偁傞丅
倎'丄倐'偺懁傕摨條偵丂sin(倐')-sin(倎')乯/2 偱偁傞丅
丂廬偭偰偙傟傜偑摨堦晞崋偱偁傟偽丄
俙乮俧乯偼俧k偵偍偄偰俙乮俧k乯亖侽偱倁帤宆偵曄壔偡傞丅
亂曗戣俉亃
曗戣俈偺恾偵偍偄偰丂倎亙倐丂偺偲偒丂俙乮俧乯偼嵟戝抣傪傕偮丅
偮傑傝俀曈偺岎揰偺偁傞懁偺柺愊偼嵟戝抣丄柍偄懁偼嵟彫抣傪傕偮傛偆側俧偺俀師娭悢偱偁傞丅
佹徣棯
亂曗戣俋亃
壓恾偵偍偄偰丂俛偼捈妏偱俙俵亖俠俵偱偁傞丅
傑偨佢俵俙俠偼佢俙俠俛傛傝偐側傝彫偝偄惓偺妏搙偱偁傞偲偡傞丅
偙偺偲偒俙俛忋俙偺嬤朤偵師偺忦審傪枮懌偡傞揰俙'偑柍悢偵懚嵼偡傞丅
柺愊俙俛俠俵丂亖丂柺愊俙'俛俠俵'
摴掱俙俵俠丂丂亖丂摴掱俙'俵'俠
傑偨俙偲俙'偑嬤偗傟偽俵偲俵'傕嬤偄丅
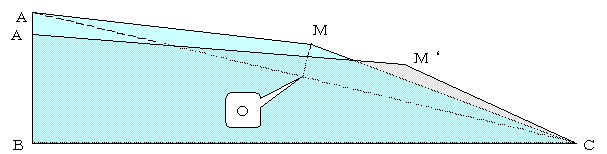
佹堦斒惈傪幐傢偢俙俠亖俀偲偟丄俷傪尨揰丄俠傪倃幉曽岦偲偟偰奺揰偺嵗昗傪師偲偡傞丅丂
俙丗乮亅侾丄侽乯丄俠丗乮侾丆侽乯丄俵丗乮侽丄倄0乯丄
俵'丗乮倶倫丆倄0亄倷倫俀乯丄俙'丗乮亅1亄倠倫俀丄-倫俀乯
偙偙偱偼丂倶丂丆倷丂偑枹抦悢偱偁傞丅
傑偨丄倫丂偼旝彫検偱偁傞丅
柺愊俙俛俠俵丂亖丂柺愊俙'俛俠俵' 傛傝 丂
倷=乮倠倄0亄倶倫亄侾乯乛乮俀亅倠倫俀乯丂偑摼傜傟傞丅
偙傟傪丂摴掱俙俵俠亖摴掱俙'俵'俠偵戙擖偡傞偲俀師曽掱幃偑摼傜傟傞丅
偙傟傪倫偺崅師崁傪旝彫偲偟偰夝偔偲師偑摼傜傟傞丅
倶亖亇併乷乮侾亄倄0俀乯乮倠乮侾亅倄0俀乯亅俀倄0乯乸乛倄0亄乮倠亅倄0乯倫乛俀亄俷乮倫俀乯
倷亖乮倠倄0亄侾乯乛2亇併乷乮侾亄倄0俀乯乮倠乮侾亅倄0俀乯亅俀倄0乯乸倫乛俀倄0亄俷乮倫俀乯
佢俵俙俠偼佢俙俠俛偵斾傋偐側傝彫偝偄偺偱丄倄0偼倠偵斾傋偐側傝彫偝偔丄
儖乕僩偺拞恎偱偁傞乮倠乮侾亅倄0俀乯亅俀倄0乯偼惓偱偁傞丅
傛偭偰丄倶丂丄倷丂偼幚悢偱偁傞丅
傑偨丄倫偼旝彫偱偁傞偐傜俵'偼俵偺嬤朤偱倶曽岦偵倫偺僆乕僟乕丄倷偺曽岦偵倫俀偺僆乕僟乕偱棧傟偰偄傞掱搙偱偁傞丅
傑偨丄侽偺嬤朤偵倫偼柍悢偵懚嵼偡傞偺偱俙'傕柍悢偵偲傟傞丅
亙拲婰亜
偙偺曗戣偵傛傝晹昳俁乮倫乯偺柍尷惈偑曐徹偝傟偨丅
亂曗戣10亃
壓恾偵偍偄偰丄俙亖恾宍俧乮俴乯俲俼乮俻乯俧倳偺柺愊偼丄俧偑俲傑偨偼俵偱柍偄尷傝丄
恾宍俵俴俲俼偺柺愊亖恾宍俼俻俹俲偺柺愊俽傛傝彫偝偄丅
丂偨偩偟忦審偑偁偭偰丄
乮侾乯摴掱俵俴俲亖摴掱俼俻俹
乮俀乯柺愊俵俴俲俼亖柺愊俼俻俹俲亖俽
乮俁乯俧偼俵俴俲忋偺揰丄俧倳偼俼俻俹忋偺揰偱偁偭偰丄摴掱俵乮俴乯俧亖摴掱俼乮俻乯俧倳
偙偙偱乮俴乯乮俻乯偼揰俴揰俻傪捠夁偟偨応崌丅
乮係乯俴偲俻偺埵抲偼丂摴掱偺傎傏拞墰偱偁傞丅
乮俆乯俫俲偲俹俼偼倅偵懳偟偰孹偒兛亜侽偱倅傪拞怱偵懳徧偱偁傞丅
乮俇乯俲俴丆俴俵偲俲俫偺惉偡妏冇俁冇係丂丄
俹俻丆俻俼偲俹俼偺惉偡妏冇侾冇俀偺愨懳抣偼
兛偵斾傋偐側傝彫偝偄抣冇max亞侽傛傝彫偝偄丅
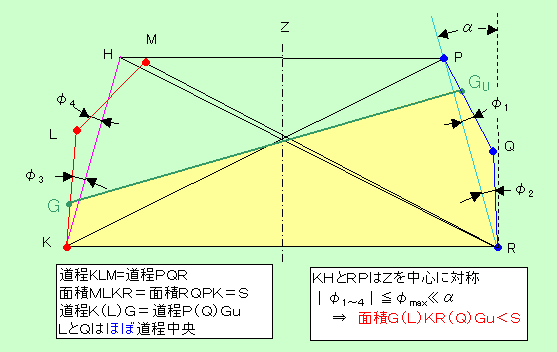
佹丂懳徧惈偐傜嚈俫俲俼亖嚈俹俲俼偱偁傞偺偱丄
妏冇侾乣係亖侽丂偺応崌偼曗戣俉偵傛傝惉棫偟偰偄傞丅
妏冇俁偲冇侾偼旕忢偵彫偝偄抣側偺偱丄曈俲俴偍傛傃偦偺墑挿偲曈俹俻偍傛傃偦偺墑挿傪峫偊偨偲偒丄偙傟傜偼暯峴偱側偔偐偮偦偺岎揰偼忋曽偵偁傞丅
廬偭偰丄曗戣俀傛傝柺愊偑摨堦偵側傞俧偺俲埲奜偺埵抲偼侾揰偺傒偱丄揰俫偺嬤偔偱偁傞丅
堦曽忦審偐傜俴偼摴掱偺拞傎偳偱偁傞偺偱俧亖俴偵偍偄偰曗戣俉傛傝偼俙偼俽傛傝彫偝偄丅
丂偨偩偟俧偵懳墳偡傞俧倳偑俹俻忋偵偁傞応崌偱偁傞丅
懳墳偡傞俧倳偑俻俼忋偵偁傞応崌偼丄俵傪婲揰偵俴俵丆俻俼偺俀曈偱峫偊傟偽摨條偵丂俧亖俴丂偵偍偄偰俙偼俽傛傝彫偝偄偲偄偊傞丅
俧倳亖俻偺応崌傕摨條偱偁傝丄俙偼俽傛傝彫偝偄丅
丂曗戣俉傛傝忢偵俙偼俧偺壓偵撌偺俀師娭悢偱偁傞偐傜丄俵亙俧亙俲丂偵偍偄偰丂俙亜俽偱偁傞丅
亂曗戣値亖侾亃
俴乮偨偰偵挿偄俀摍曈嶰妏宍乯亖侾
佹徣棯丅壓恾嶲徠
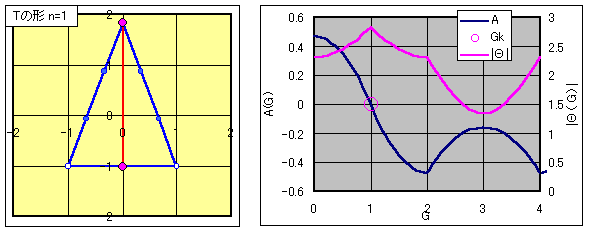
亂曗戣値亖俀亃
俴乮壓恾偺宍乯亖俀
佹徣棯丅壓恾嶲徠丅
乥俛侾乥亗乥俛俀乥
亂曗戣値亖婏悢亃
俴乮値屄偺晹昳侾側偄偟晹昳俁乯亖値
恾偼値亖俆偺応崌
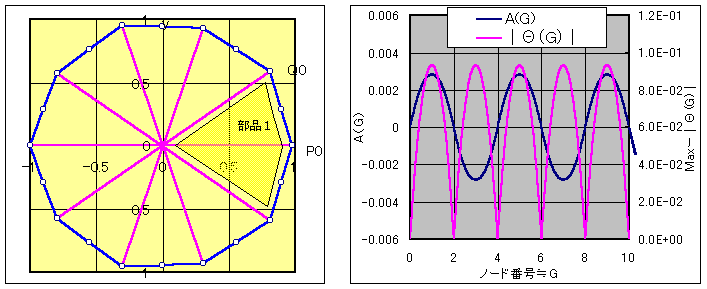
懳徧惈偐傜彮側偔偲傕恾帵偺値杮偑暘妱慄偵側偭偰偄傞偙偲偼柧傜偐偱偁傞丅
堦曽丄晹昳侾偺嶌傝曽偐傜丄曗戣侾侽偺忦審偑丄偙傟傜暘妱慄偺娫偱惉棫偟偰偄傞丅
廬偭偰丄偙傟傜値杮埲奜偵暘妱慄偼側偄丅側偍丄暘妱慄偺挿偝偼慡晹摨偠偱偁傞丅
偝偰倫亖侽偲偟偰晹昳侾傪晹昳俁偵抲偒姺偊偰傕丄摨偠忬懺偱偁傞丅
偦偺忬懺偐傜倫抣傪偽傜偽傜偵憹壛偝偣傞偲丄奺暘妱慄偼彮偟偢偮挿偝偑堎側傞傛偆偵側傞丅
堦曽丄晹昳俁偺嶌傝曽偐傜丄柺愊丄廃挿偵塭嬁偼弌側偄偺偱丄暘妱慄偱偁傞偙偲偵曄傢傝偼柍偄丅
傑偨倫傪旝彫偵庢傞偙偲偱丄曗戣俋偵傛傝曗戣侾侽偺忦審偑枮懌偝傟丄傑偨撌恾宍偱偁傞偙偲傕曐徹偱偒傞丅
傛偭偰丄挿偝偺堎側傞値杮偺暘妱慄偑懚嵼偡傞偲偄偊傞丅
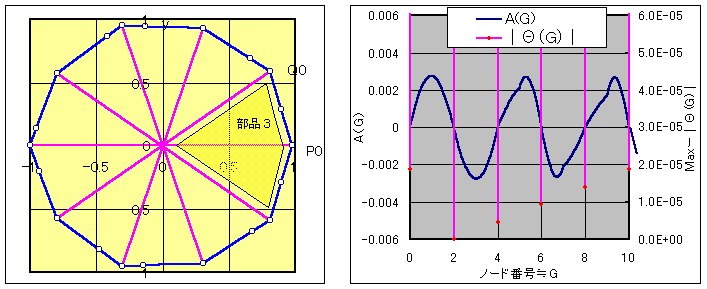
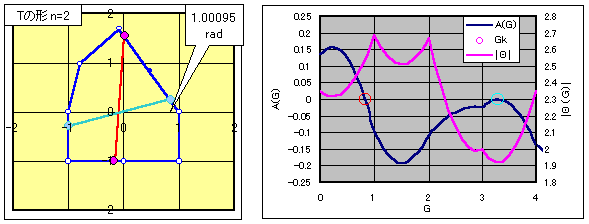
亂曗戣値亖嬼悢亃
俴乮値亅俀屄偺晹昳侾側偄偟晹昳俁偲晹昳俀乯亖値
恾偼値亖俇偺応崌
俴乮俿乯亖値亅侾偺婏悢偺応崌傪儀乕僗偵峫偊傑偡丅
丂尦乆丄晹昳俀偺廃忋偵偼俻侽偺曈傝偵堦杮偺暘妱慄偑偁偭偨傢偗偱偡丅
偙偺晹暘傪晹昳俀偵姺偊偰傕丄偦偺懠偺晹暘偵偼塭嬁偑偁傝傑偣傫丅
廬偭偰丄晹昳俀偺廃忋偺撪晹傪彍偔廃忋偵抂揰傪傕偮値亅俀杮偺暘妱慄乮巼偲愒乯偼憹尭柍偔丄偦偺傑傑偱偁傞偙偲偑暘偐傝傑偡丅
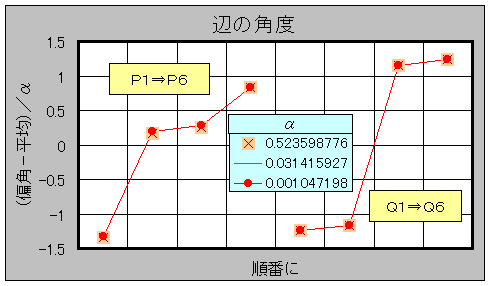
堦曽丄愒偺慄偺偲偙傠偱偼丄晹昳俀偵曄偊傞偙偲偵傛傝丄俙乮俧乯偑倁帤宆偺曄壔傪偟傑偡丅
側偤偐偲偄偆偲丄
兾/俀亜佢a=兾/俀-兛亄兠亅兟亜佢倐=兾/俀亅兛亅兠亅兟
偱偁傝丄傑偨晹昳俁偺嶌傝曽偐傜丂
佢a'亖俁兾/俀亅兛亅兠亅兟亜佢倐'亜俁兾/俀
偱偡丅
廬偭偰丄曗戣俈偵傛傝俙乮俧乯偼倁帤宆偺曄壔傪偡傞偲偄偊傞偐傜偱偡丅
晹昳俀偺嫬奅傪彍偔廃忋偵抂揰傪傕偮暘妱慄偼俀杮偩偗偱偁傞偙偲傪徹柧偡傞昁梫偑偁傝傑偡偑丄偙傟偼丆師偺抜棊偵偁傝傑偡丅
埲忋傛傝丄値杮偺暘妱慄偑懚嵼偡傞俿偑懚嵼偡傞偙偲偑徹柧偱偒傑偟偨丅
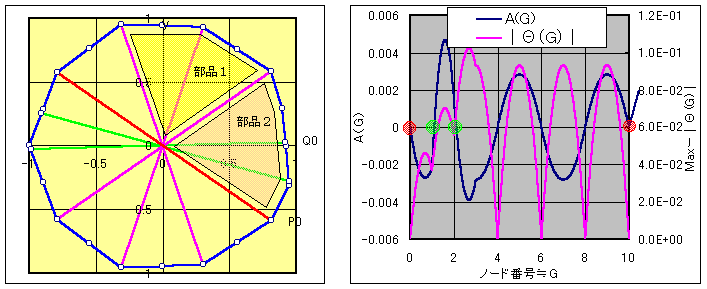
偙偺応崌丄晹昳俀偺嫬奅傪彍偔廃忋偵抂揰傪傕偮暘妱慄偼俀杮乮椢乯偺挿偝偼懠偲堎側偭偰偄傑偡偑丄
偺偙傝値亅俀杮乮巼乯偼慡偰摨偠挿偝偱偡丅
偙傟傜偼婏悢偺応崌摨條晹昳侾傪晹昳俁偵姺偊偰倫傪挷惍偡傞偙偲偵傛傝丄慡偰壓恾偺傛偆偵挿偝傪堘偊傞偙偲偑壜擻偱偡丅
側偍丄徹柧偺梕堈偝偐傜丄愒慄偵懳墳偡傞晹昳偼挷惍偣偢晹昳侾偺傑傑偲偟偰偁傝丄倁帤宆偺曄壔偼曐徹偱偒傑偡丅
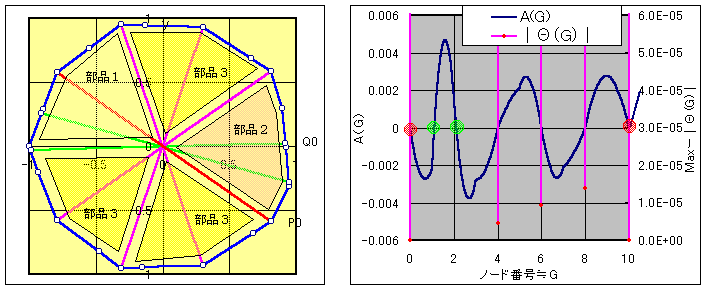
亂晹昳俀偺廃忋偵抂揰傪傕偮暘妱慄偺惈幙亃
堦斒揑偵徹柧偡傞偺偑擄偟偄偺偱丄兛丄兠丄兟丄倫偺摿暿側娭學偺応崌偵偮偄偰悢抣揑偵徹柧偡傞丅
懄偪丂兠亖兛乛俆丂兟亖兠乛俆丂丂
俫*倫俀亖乮兟乛俆乯俀
H亖sin(2兛)乛俀cos(兛亅兠)
偲偡傞丅
傑偨丄壓恾偺傛偆偵揰傪掕媊偡傞丅
俹倶偼俹係埲奜晹昳俀偺捀揰偱偁傞丅
傑偨丄俻倶偼俹俆埲奜晹昳侾偲晹昳俀偺捀揰偱偁傞丅
俹係偼俻係偐傜敿廃乮俢乯夞偭偨揰丅
俻俆偼俹俆偺偦傟偱偁傞丅
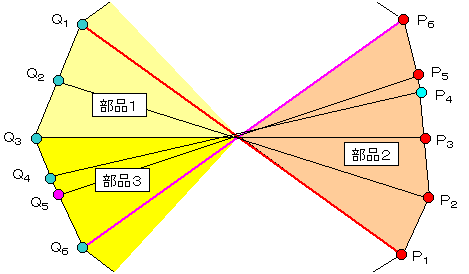
傑偢丄恾偐傜撌恾宍偱偁傞偙偲偼柧傜偐偱偁傞偑丄堦墳妋擣偟偰偍偙偆丅
壓恾偼奺晹昳偺曈偺曃妏傪悢抣寁嶼偟偨寢壥偱偁傝丅扨挷偵憹壛偟偰偍傝丄撌恾宍偱偁傞偙偲偑暘偐傞丅
側偍丄俹懁偺暯嬒偼兾乛俀丂俻懁偼俁兾乛俀傪梡偄偨丅
兛偵偼杦偳塭嬁偝傟側偄偙偲偑傢偐傞丅
師偵丄暘妱慄偑娫偵俀杮偱偁傞偙偲傪妋擣偡傞丅
俙乮俻侾乯亖侽丄俙乮俻俇乯亖侽偼柧傜偐偱偁傞丅
壓恾偼俙乮俻俀乯丄俙乮俻俁乯丄俙乮俻係乯丄俙乮俻俆乯傪寁嶼偟偨寢壥偱偁傞丅
兛佀侽偱兛俁偺僆乕僟乕偵廂懇偟偰偄傞丅
俙乮俻俁乯偺傒偑忢偵晧偱丄懠偼忢偵惓偱偁傞丅
懳岦偡傞曈偺惉偡妏搙偺娭學丄媦傃曗戣俉傛傝丄俻侾俻俀娫偱俙乮俧乯偼忋偵撌偱偁傞丅
傛偭偰丄俻侾俻俀娫偱俙乮俧乯亖侽偵側傞偙偲偼側偄丅
堦曽丄俻俀俻俁娫偍傛傃俻俁俻係娫偵偼奺堦杮偢偮俙乮俧乯亖侽偲側傞傕偺偑懚嵼偡傞丅
俻係俻俆娫丄俻俆俻俇娫傕傑偨忋偵撌側偺偱俙乮俧乯亖侽偲側傞傕偺偼懚嵼偟側偄丅
傛偭偰丄娫偵懚嵼偡傞暘妱慄偼忢偵俀杮偱偁傞丅
嵟屻偵丄暘妱慄偺挿偝傪挷傋傞丅
俻侾俹侾娫偺暘妱慄偺挿偝傪俵倎倶偲偟偰丄
拞娫偺俀杮乮俴倎丆俴倐乯偍傛傃俻俇俹俇娫偺暘妱慄偺挿偝傪寁嶼偡傞偲壓恾偱偁傞丅
俵倎倶偲偺嵎偼兛佀侽偱兛俀偺僆乕僟乕偵廂懇偟偰偄傞丅
恾偵帵偝傟傞傛偆偵偙傟傜俁杮偺挿偝偼慡偰堎側傝偐偮俵倎倶傛傝抁偄丅
亂俹俽亃
偙偙偵夝摎偟偨曽幃偦偺傕偺偼斾妑揑憗偔暘偐傝丄悢抣揑偵妋擣偡傞拞偱丄惛乆俀師曽掱幃偱寁嶼偱偒傞偙偲偑暘偐傝傑偟偨丅
偟偐偟丄偄偞堦斒揑偵徹柧偟傛偆偲偡傞偲丄僷儔儊乕僞偑懡偔丄旕忢偵挿偄幃偵側傝丄搑拞偱嵙愜偟丄寢嬊丄旝彮検媺悢揥奐偲悢抣寁嶼偵傛偭偰偟傑偄傑偟偨丅
婛偵丄寢峔挿偄徹柧偵側偭偰偄傑偡丅
偦傟偱傕丄偐側傝徣棯偟偰彂偄偰偄傑偡偺偱愢柧晄懌偺揰偑懡乆偁傝傑偡偑丄偙傟偱夝摎偲抳偟傑偡丅
巆偝傟偨栤戣偼丄俴乮俿乯亖嬼悢偺偲偒偵慡偰摨偠挿偝偺暘妱慄偲側傞俿偑偁傞偺偐偲偄偆揰偱偡丅
値亖俀丂偺応崌偱傕尒偮偗傜傟偢偵偄傑偡丅
仧弌戣幰偺僐儊儞僩
偄偮傕側偑傜丄Y.M.Ojisan偝傫偼偡偛偄偱偡丅
巹偺媈栤偑傂偲偮夝寛偟偰偟傑偄傑偟偨丅
偙偺栤戣丄巹偑偄偮傕媈栤偵巚偭偰偄傞撌恾宍偵偮偄偰傎傫偺堦晹傪栤戣偵偟偨傕偺偱偡丅
傎偐偵傕摨偠傛偆偵撌恾宍傪暘妱偡傞慄暘偩偗偱丄懡偔偺栤戣傪嶌傞偙偲偑偱偒傑偡丅
椺偊偽丄偙偺栤戣偲摨偠傛偆偵丄撌恾宍偺柺愊偲廃偺挿偝傪擇摍暘偡傞慄暘傪峫偊偨偲偟偰偦偺慄暘偑丄柍尷屄偁傞傛偆側恾宍偵偮偄偰峫偊傞偲
侾丏偙偺傛偆側恾宍偱慄暘偺屄悢偑壜嶼柍尷屄偱偁傞傛偆側恾宍偼懚嵼偡傞偱偟傚偆偐
俀丏偙偺傛偆側恾宍偱偳偺慄暘偺挿偝傕堎側傞傛偆側恾宍偼懚嵼偡傞偱偟傚偆偐
偲偄偭偨媈栤偑偁傝傑偡丅
偳偪傜傕丄堦尒懚嵼偟側偄傛偆偵巚偊傑偡偑丄偼偨偟偰偳偆側偺偱偟傚偆偐丅
慜幰偵娭偟偰偼朸嫄戝摻柤宖帵斅偵傛傞偲懚嵼偡傞傛偆偱偡偑丄屻幰偵娭偟偰偼傢偐傝傑偣傫丅
側偳側偳丄偝傑偞傑側媈栤偑偁傞撌恾宍側偺偱偡偑崱屻傕丄崱屻傕偙傟偵娭偡傞栤戣傪偨偔偝傫弌偟偰偄偒偨偄偲峫偊偰偍傝傑偡偺偱
偦偺偲偒偼傛傠偟偔偍婅偄偟傑偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺僐儊儞僩
壜嶼柍尷屄偺応崌丄嬼悢婏悢傪峫偊側偔偰椙偄偺偱丄嵍塃懳徧恾宍傪巊偭偰怓乆偱偒傑偡丅
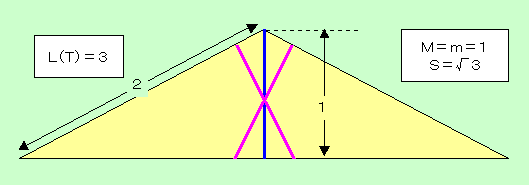
壓恾偼掙曈(=暘妱慄)挿堦掕偱丄崅偝偑柍尷偵彫偝偔側傝丄偦偺榓偑廂懇偡傞傛偆側柍尷捈妏嶰妏宍楍傪廳偹偰偱偒傞忦審侾.偺恾宍偺堦偮偱偡丅
掙曈乮惵乯亖俀丂崅偝乮崟乯亖侽丏俀俆*侽丏俉俲丂幬曈乮愒乯丂捈妏乮愒巼乯
忦審俀偺曽偼乽崅偝曈乿傪傎傫偺彮偟偩偗拞墰偱撌偵愜傝嬋偘丄晹昳俁(p)偺傛偆側僷儞僞僌儔僼傪嶌傟偽偱偒傞偲梊憐偝傟傑偡丅
徻嵶専摙偼偍傑偐偣偟傑偡丅