◆広島県 清川 育男 さんからの解答。
(1) 14通り。
(2) 41通り。
(3)
a3=1
an=3×an−1−1
an=1/2×(3n-3+1)
左右対称の綺麗な式の表現が解りません。
左右対称の綺麗な式に表現出来ないと言うことは、間違っているのでしょうね。
【コメント】
(1)は正解です。
(2)は誤りです。
七角形の場合は、a7=42になるはずです。
ちなみに八角形はa8=132です。
この問題は苦戦されている方が多いようなので、ヒントを追加します。
anをan−1で表すのではなく、a2からan−1で表すのがミソです。
例えば、二角形?は1、三角形は1、四角形は2、五角形は5
a5=5=1×2+1×1+2×1ですから、
この式をa2=1,a3=1,a4=2を用いて表すことができると思います。
六角形a6=14ですから、同様にa1〜a5を用いて表すことができます。
◆広島県 清川 育男 さんからの解答。
ヒントを手がかりに推理しました。
階差数列になるかどうかもわかりません。
仮に階差数列になったとしても、一般式は7次元以上が予想されます。
信じられないような綺麗な式が予想されます。
(3)
a4
=a3×a2+a2×a3
=1×1+1×1
=2
a5
=a4×a2+a3×a3+a2×a4
=2×1+1×1+1×2
=5
a6
=a5×a2+a4×a3+a3×a4+a2×a5
=5×1+2×1+1×2+1×5
=2×7
=14
a7
=a6×a2+a5×a3+a4×a4+a3×a5+a2×a6
=14×1+5×1+2×2+1×5+1×14
=42
a8
=a7×a2+a6×a3+a5×a4+a4×a5+a3×a6+a2×a7
=42×1+14×1+5×2+2×5+1×14+1×42
=42+14+10+10+14+42
=2×66
=132
以上です。
信じられないような数の規則性というか神秘性を感じます。
先生がヒントを出したくなる気持ちがわかるような気がします。
自信作ですね。感激しております。
【コメント】
今度は見事正解です。
回帰的な公式になるのが面白いところですね。
これを証明するには、数学的帰納法が有効かもしれません。
五角形を求めるには四角形の結果を(五角形を四角形と一つの三角形に分ける)、六角形を求めるには五角形の結果を(六角形を五角形と一つの三角形に分ける)と必ず前の結果が利用できるはずですから。
◆広島県 清川 育男 さんからの解答。
数列の帰納的定義で、わかさひ君さんが触れておられる数列サイトに、この問題の一般項と、この数列になる実例が紹介されています。
Catalan mumbersと言うそうです。
| an= | 2nCn ――― n+1 | = | 2n! ―――――― n!(n+1)! |
n=5
| a5= | 10! ――――― 5!×6! | =42 |
n=6
| a6= | 12! ――――― 6!×7! | =132 |
【コメント】
これはあまりにも美しい公式ですね。
思わず感動しました。
◆石川県 青木からの解答。
この問題はL・オイラーが1751年にゴルトバッハへの手紙の中で示したものだそうです。
の式を証明します。
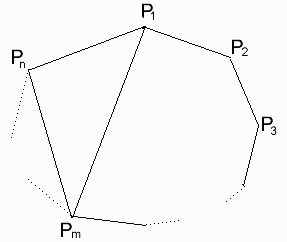
多角形Tn=P1P2P3・・・Pnとします。
対角線P1PmとPmPnによって、Tnは次の3つの部分に分割されます。

ここでmを固定して考えると、
Tmの分割される数はam、
Tn+1-mの分割される数はan+1-mとなる。
したがって△P1PmPnを含むTnの分割は
am×an+1-mとなる。
Tnを分割したものには必ず△P1PmPnのどれかが含まれるから、ここでmを2からn−1まで変化させると、