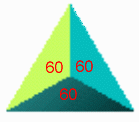
正四面体（４つの正三角形でできている立体）の一つの頂点には、正三角形が３つ集まっています。前回に続いて多面体の性質に挑戦します。
正多面体の面、辺、頂点の数を表にまとめてみます。
| 正多面体 | 面(Face) | 辺(Edge) | 頂点(Vertex) |
| 正四面体 | ４ | ６ | ４ |
| 正六面体 | ６ | １２ | ８ |
| 正八面体 | ８ | １２ | ６ |
| 正十二面体 | １２ | ３０ | ２０ |
| 正二十面体 | ２０ | ３０ | １２ |
【問題１】
正多面体の面の数、辺の数、頂点の数のうち、２つがわかれば残りの一つは計算で求めることができます。
例えば、面の数と頂点の数がわかれば、辺の数はすぐわかります。
正多面体の面の数、辺の数、頂点の数の間にはどんな関係がありますか。
(オイラーの多面体定理といい、任意の多面体で成り立ちます。)
正四面体（４つの正三角形でできている立体）の一つの頂点には、正三角形が３つ集まっています。
６０×３＝１８０度。
３６０度になれば平面ですが、
３６０−１８０＝１８０度不足しています。
このことを正四面体の一つの頂点の尖度（とがっている程度）は１８０度ということにします。
もちろん平面は尖度０ですし、この数字が大きいほど、その頂点はとがっていることになります。
正六面体（立方体）の頂点の尖度は、頂点に９０度が３つ集まっているので
３６０−９０×３＝９０度です。
正四面体の方が、尖度が大きいです。
確かにさわったとき、正四面体の方が痛そうですね。
また頂点は全部で８個あり、各頂点の尖度は同じですから、全ての頂点の尖度の合計は
９０×８＝７２０度です。
【問題２】
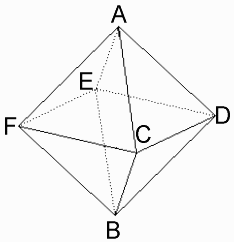正八面体の頂点の尖度と、全ての頂点の「尖度の合計」を求めてください。
【問題３】
正十二面体の頂点の尖度と、全ての頂点の「尖度の合計」を求めてください。
【問題４】
正多面体の全ての頂点の「尖度の合計」にはどんな性質があるでしょうか。
【おまけ】
任意の多面体で、「尖度の合計」に問題４の関係が成り立つことを示してください。
マウスをドラッグする（ボタンを押しながら動かす）と正六面体が回転します。
問題１〜４のいずれかができれば正解とします。
◆解答用紙はこちらです。
| No. | 解答時刻 | 正解者 | |
| １ | 2/21 SUN 0:10 | 溝部 光洋 さん | 一般 |
| ２ | 2/21 SUN 0:33 | タケヒロ さん | 一般 |
| ３ | 2/21 SUN 0:36 | Asami さん | 一般 |
| ４ | 2/21 SUN 1:09 | Miki Sugimoto さん | 大学生 |
| ５ | 2/21 SUN 6:43 | 清川 育男 さん | 一般 |
| ６ | 2/21 SUN 6:47 | ネットＯＬ さん | 一般 |
| ７ | 2/21 SUN 10:05 | 松井 恵宣 さん | 一般 |
| ８ | 2/21 SUN 10:36 | 平田 和弘 さん | 一般 |
| ９ | 2/21 SUN 13:11 | 吉田 和義 さん | 一般 |
| 10 | 2/21 SUN 15:38 | Yasuharu Matsumoto さん | 小学生 |
| 11 | 2/21 SUN 22:11 | ひろし さん | 一般 |
| 12 | 2/22 MON 16:13 | Dr. Berserker さん | 大学生 |
| 13 | 2/26 FRI 13:01 | せいちゃん さん | 一般 |
| 14 | 2/27 SAT 22:21 | 中村屋ー さん | 中学２年 |
| 15 | 2/18 TUE 12:24 | kitty さん | 中学２年 |
| 16 | 1/ 4 TUE 17:44 | ken さん | 一般 |
◆過去問はこちらです。
◆ 今週の問題へ
数学の部屋へもどる。