『区別のない整理箱』

【問題１】

　区別のできない玉４個と箱４箱があります。
このとき箱に玉を入れるパターンは何通りあるでしょうか。
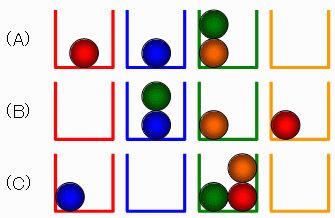
下図例で　（A）と（C）は違うパターンですが、（A）と(B)は同じパターンです。

【問題２】

区別のできない玉４個と箱４箱があり、その各箱には区別できない袋が４袋入っています。
このとき玉を袋に入れるパターンは何通りあるでしょうか。
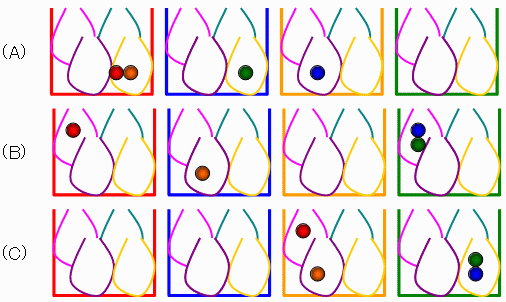
下図で（A）と（C）は違うパターンですが、（A）と(B)は同じです。

【問題３】

区別のできない玉４個と箱４箱があり、その各箱には区別できない袋が４袋入っています。
さらにその各袋には区別できない小袋４袋が。。。。とN段続くとき、玉を入れるパターンは何通りあるでしょうか。
問題１をN=1　問題２をN=2とします。

【問題４】

玉、箱、袋。。。が５個、５箱、５袋、。。。N段の場合のパターンは何通りあるでしょうか。

【問題５】

玉、箱、袋。。。がM個、M箱、M袋、。。。N段の場合のパターンの数をP（M,N）とするとき、
P(M,N)はNのM－１次多項式であることを証明してください。

【研究問題】

P(M,N)の一般式を求めよ。
ないし任意特定のMに対して、P(M,N)を求めるできるだけシンプルなプログラム（or フローチャート）を示せ。