東京都の中学校3年生 もやし さんからの問題です。
中学数学の範囲だけで解いてください。
パラボラアンテナとは、放物線を対称の軸を回転軸として回転させてできる回転体です。
パラボラアンテナには、軸に平行に飛んできた音などを軸上の1点に集める性質があります。
また、その点から発した音などは、パラボラアンテナの面に反射して、軸に平行に飛んでいきます。
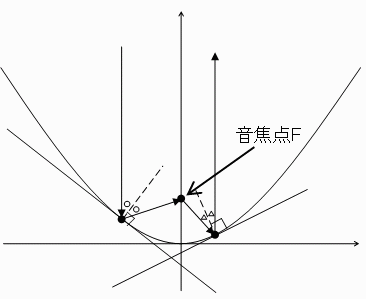
図は、パラボラアンテナを軸を含む平面で切ったときの断面図をxy座標に置いたもので、放物線の頂点は原点に一致します。

y軸に平行に飛んできた音は、放物線との交点における放物線の接線に反射します。
どの点からy軸に平行に飛んできても、全て1点で交わります。
その点を音焦点Fと呼ぶことにします。
また、点Fから放物線に向けて出た音は、前記のように反射し、y軸に平行に飛んでいきます。
これをもとに、次の問に答えてください。
できれば答えだけはなしにして下さい。
【問題1】
放物線y=x2上の点(1,1)における接線の方程式を求めてください。
【問題2】
放物線y=x2の音焦点Fの座標を求めてください。
【問題3】
放物線y=ax2の音焦点Fのy座標をfとするとき、fをaの式で表してください。