2
◆東京都 哲(サトシ) さんからの解答。
【問題2】
| A(- | 1 2 | ,0), B( | 1 2 | ,0), p≧0, q≧0 として、 |
(r-p)2+(s-q)2=1 を満たす点 S(r,s) とすると、
R の位置に関わらず、AR+RS+SB≧2 とすることができ、
R を固定し S を動かしたとき、AR+RS+SB や AS+SR+RB は連続的に変化するから、
AR+RS+SB または AS+SR+RB の最小値が2以下であればよい。
p≧0 より、最小値が小さくなるのは AS+SR+RB の方で、このとき RA 向きと RS 向きは一致する。
AR 間距離を a 、BR 間距離を b と置く。
(i) a≦1 のとき、AS+SR+RB の最小値は b-a+2 となり、
これが2以下のときは、b≦a すなわち常に満たす。
(ii) a≧1 のとき、AS+SR+RB の最小値は a+b となり、
| これが2以下のときは、楕円 x2+ | 4 3 | y2=1 の周上及び内部。 |
以上(i)(ii)、また対称性より、P または Q の存在する領域は、
| 「楕円 x2+ | 4 3 | y2=1 の周上及び内部」...(*)である。 |
また、(*)の任意の2点を線分で結んでも、その線分は(*)からはみ出すことはないから、 結局題意を満たす線分の通過する領域は(*) であり、
| その面積は | 2 | である。 |
# 線分なのに楕円になるらしい。
ちょっと奇妙です。
◆山梨県 Footmark さんからの解答。
【問題2】
点P点Qを長さ1の頑丈で変形しないストロー(図の緑線)の両端とする。
長さ2の糸をそのストローに通してから、糸の両端を距離が1である2定点A,Bに固定する。
ストローを持って糸が弛まないようにすると、AP+PQ+QB=2 となり条件を満たす。
そこで、ストロー内にある糸の部分を固定して考えると、
(1) AP≦QB のとき、ストローの端Qを最大にA点から遠ざけると、APとPQが同一直線上になり、
(2) AP≧QB のとき、ストローの端Pを最大にB点から遠ざけると、QBとPQが同一直線上になる。
つまり、
AP,QBの長い方の糸に連結しているストローの端を、2定点A,Bのどちらからも最大に遠ざけると、
AP,QBの短い方の糸がストローと同一直線上になる。
明らかに、P点やQ点が2定点A,Bのどちらからも最大に遠ざかるのは、(1)や(2)のときである。
結局、
AP≦QBのときA,Q間を最大にすると、Q点は2定点A,Bからの距離の和が常に2であり、
AP≧QBのときB,P間を最大にすると、P点は2定点A,Bからの距離の和が常に2である。
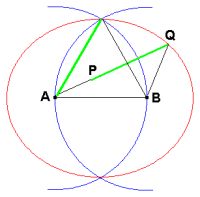
それ故、ストローは図の赤い楕円内に常にある。
明らかに、この楕円の長軸の長さは2で短軸の長さは![]() である。
である。
| よって、領域の面積=π・ | 長軸の長さ 2 |
・ | 短軸の長さ 2 |
= | 2 |
π |
◆愛知県 Y.M.Ojisan さんからの解答。
【問題4.1】
(1)2点 (2)1辺
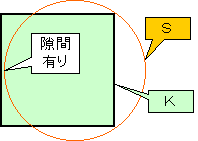
Kの辺長を1とし、Sの直径をDとするとき
| 1= | πD3 6 |
よりD=1.2407...である。 |
【問題4.2】
(1)3点 (2)3辺
Kの辺長を1とし、Sの直径をDとするとき
| 12+5 12 |
= | πD3 6 |
より |
| D< | 1+ 2 |
=1.6180...であるので、 |
なお、体積公式など下記を利用させていただいた。
http://www2.tokai.or.jp/yosshy/20_vol.htm
◆出題者のコメント。
問題2はお二人とも正解です。
私は問題をつくるとき、Footmarkさんの解答と殆ど同じような発想でやっていました。
しかしストローとは表現がうまいですね。
問題4ですが、Y.M.Ojisanさん、両方とも(1)は正解です。
それで、(2)ですが問題が間違っていました。
すいませんでした。
「最大何本の辺を含めるか?」ではなく、正しくは
「最大何本の辺と交わることが出来るか?」でした。
(そうでないと(1)と殆ど同じ問題になってしまいますし。)
◆愛知県 Y.M.Ojisan さんからの解答。
【問題4.1】
(2)5辺
(1)より5辺以上は明らか。
また遠い方の平行2辺の距離は![]() >Dであるから6組の平行2辺の各組において両方と同時には交差できない。
>Dであるから6組の平行2辺の各組において両方と同時には交差できない。
よって6辺以下である。
ところが近い方の平行2辺に接し、これらに交わらない向かい側の直交1辺に接する球面の直径は計算すると
5/4=1.25>Dである。
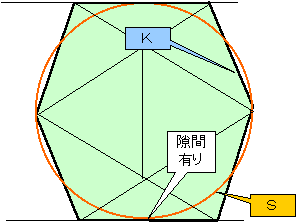
よって6辺は不可能である。一例を下図に示す。
チョッと出ているのが交差する辺であり、球面より外に出ている部分を拡張表現してある。
マウスで回ります。
 |
【問題4.2】
(2)15辺
| 一番遠い(実は唯一の)平行2辺の距離は | 1+ 2 |
>Dであるから |
 |
実はオーラは感じていました。
こちらの問題のほうで答えを最初は考えていました。
1.6180 と 1.6092 , 1.2500 と 1.2407 の近さは不思議で興味深いです。
◆出題者のコメント。
見事正解です。
分かりやすい図までありがとうございます。
正多面体は5つしかないので、一般化も何も無いのがちょっと残念です。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題3】
平面α上で考察するのが順当な方法でしょう。
しかしここでは逆に空間に広げて考えてみます。
即ちαに直交する方向にその円をスイープし、直円柱にして考えます。
すると、下図のように水平に設置したA,Bを支点とする丸太のシーソーの表面上にC君とD君が座っている(ないしぶら下がっている)状態(傾きと太さ)が存在するか。
それは何種類かという問題になります。
なお条件として直円柱の軸はABの垂直2等分面内になければなりません。
また一般性を失わずにAB=2とします。
各面が鋭角三角形の条件はC,DがA,Bをそれぞれ通りABに直交する面U,Vの間にいること。
適当に回すことにより、ABを通る水平面より上部にいること。
ABを極軸とする球(半径1)の外にいること。
およびABCDは同一面上にない、
に翻訳できます。
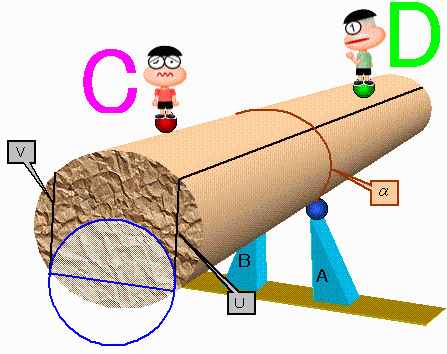
A、BとCの関係のみに着目し、シーソーの傾きθに対する丸太の半径を考えます。
θが面CABの方向のとき(θ=θ0とします。)半径は無限大です。
そこからシーソーが回転すると丸太の半径は小さくなり、ABが直径となる最小の1に達します。
ここをθ=φ+θ0とします。
その後は反対側に膨らんでθ=π/2+θ0で極大となります。
π/2+θ0を挟んで左右対称な変化をし、
最終的にθ=π+θ0で再び無限大になります。
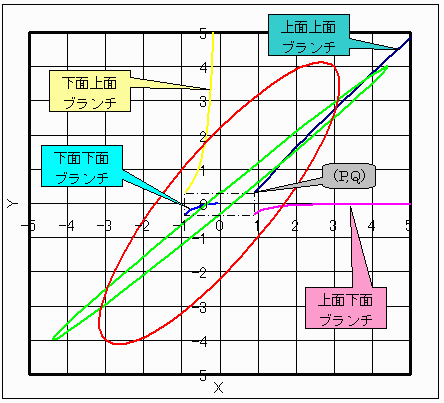
この様子を極座標(θ−θ0,r)で表すと下図になります。
ただし|θ−θ0|<φではr=1/半径として、反対側に膨らんでいることを表します。
半径は必ず1以上なので干渉することはありません。
(1)存在
ABCDは同一面上に無いので、Cのθ0とDのθ0は異なっています。
つまり(θ,r)上に両方を描けば、少なくとも1個交点があることは確かです。
すなわち少なくともそのような面αは1個あるといえます。
| 以上は頭の中のイメージで考えた存在の証明を数学風に書き下ろしてみたものです。 しかし個数はC,Dの位置がU,Vでカットされた上下面の組み合わせとして(上面上面または下面下面)と(上面下面)と(下面と上面)の3種類くらいかなと思われますが、かなり微妙であり、式を用いざるを得ません。 |
(2)個数 答え1〜3個
A,Bの座標を(0,0,±1) C,Dの座標を(xi,yi,zi) i=C,Dとします。
鋭角の条件より |zi|<1, ABCDは同一面上に無い、です。
また丸太の状態をM:(a,b,0)で表します。
ここでMは丸太の軸に直交し軸上に先端があるベクトルです。
従って丸太の半径をrとすると r2=1+a2+b2
C,DのMへの射影を X=C・M/m Y=D・M/m とします。
ここで m2=|M|2=r2−1,m≧0
鋭角の条件よりABCDは同一面上に無いので、
あきらかに(X,Y)のa,bをパラメータとする軌跡は傾いた楕円です。
実際のパラメータはatan(a/b)のみになります。
またC、Dが表面上にあることから
(X−m)2+zC2=r2 、
(Y−m)2+zD2=r2
でなければなりません。これらを開くと 定数P、Qを用いて
X2-2mX=P2=1- zC2>0 ---(1)、
Y2-2mY=Q2=1- zD2>0 ---(2)
であり、先の楕円を定数α,β、γを用いて
αX2+βXY+γY2=1 と置くことにより、
未知数 X,Y,|M|に対する3個の等式を得ます。
αX2+βXY+γY2=1に(1)(2)を代入して
X2 、Y2を消去して整理すると
α(2mX)+βXY+γ(2mY)=定数 より
(2αm+βY)(X-m)=定数-γ(2mY)-m*(2αm+βY) ----(3)
(1)よりの (X-m)2= P2+m2を使うために(3)を2乗して
(2αm+βY) 2*(P2+m2)−(定数-γ(2mY)-m*(2αm+βY))2=0
これをばらすと
(mの2次式)*Y2+(mの3次式)*Y+(mの4次式)=0
が得られる。
さらに(2)を用いてY2を消去して(Y-m)をくくりだして
(mの3次式)*(Y−m)=(mの4次式) ----(4)を得る。
(2)よりの (Y-m)2= Q2+m2を使うために(4)を2乗するとmの8次式を得る。
ところで解(X,Y,m)が得られたとき(-X,-Y,-m)も解である。
m≧0に限るのでmの解の数は4個以下である。
「(1)存在」の証明より重根を除外して実数解は奇数個である。
よって、最大3個である。
別の方法としてmをパラメータとして(1)(2)で決まる曲線(X,Y)を描くと下図です。
楕円がふっくらしている場合(赤)、予想の3ケースであることが分かります。
一方45度方向に非常に尖っている場合(緑)には、予想外の3ケースが存在します。
しかし実際に描いてみると鈍角三角形面があって解ではありません。
先の導出ではほぼ∠ABD, ∠ABC, ∠BAD, ∠BAC以外の鋭角条件を用いていないのでこれらのケースが排除できていません。
この意味(必要十分条件)では解答は不完全です。
ただ、3個まであることは確かです。
【感想】
存在までは良かったのですが、個数はいまだ発展途上で整理されていません。
一部まだエセマティックス状態ですが、答え3個は合っていると思われますので提出しました。
鋭角条件のもっと上手な使い方があるのでしょうね。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
そのような相似5角形はあるのでしょうか?
数値計算でしらみつぶしに調べてみましたが、私の理解した設定では存在しないようです。下図
まず、相似な5角形は、方向が同じか裏返しかで2通り、どの円と接するかで5通り、円の外側で接するか内側で接するかで2の5乗=32とおり、合計320通りが考えられます。
とりあえず、各辺の方向を定め、円に接するという条件で5角形を求めることができます。
相似であるためにはさらに得られた5角形の各辺の長さが等しくなければなりません。
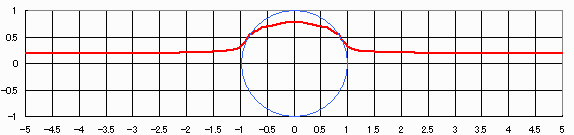
即ち最短長辺/最長辺長=1です。下図グラフ
検証していただくため、JAVAソース添付いたします。
| この図は特定の辺の方向(時間で変化)を決めたときに、中央の5角形と辺と辺の成す角が同じ順で等しく、各円に各辺が一つずつ接する5角形を全て計算し、相似に近いものから表示している図である。 同順で辺の長さが同じに最も近いものを赤、2番目に近いものを桃色で示している。 逆順は最も近いものを青、2番目を空色で示している。 グラフは最短辺の長さを最長辺の長さで割った値を示しており、1になれば緑の5角形と相似であるといえる。 なお、マウスで掴んでTOP位置の円を移動可能である。ただし正5角形位置は排除される。 また、上辺のチェックで接する5角形の表示をON/OFF可能である。 |