◆ピタゴラスのタングラム
今回のテーマは中学校３年生で習うピタゴラスの定理（三平方の定理）についてです。
ピタゴラスは孔子や老子と同時代の、紀元前６世紀に活躍した数学者です。
（Ｂ．Ｃ５８０〜５００頃）
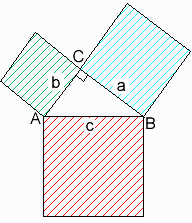
上図の直角三角形ＡＢＣで、直角を挟む辺の長さがａ，ｂ、斜辺の長さがｃであるとします。
すると
青の正方形の面積＋緑の正方形の面積＝赤の正方形の面積。つまり ａ2＋ｂ2＝ｃ2が成り立ちます。
ミュージカル「オズの魔法使い」にでてくるワラのかかしが、頭脳をはじめて授かり、最初に発した言葉が、
「直角三角形の２辺の２乗の和は斜辺の２乗に等しい。」だったそうです。
ここではこのピタゴラスの定理が人間の知恵の象徴として使われています。
【問題１】
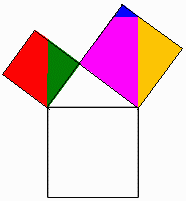上の２つの正方形を図のように分割します。
これを並び替えると、下の大きな正方形を作ることができます。
このことでピタゴラスの定理を証明してください。
回答は、並び替えた後の最も大きい正方形の各部の色を上から順に答えてもらえばＯＫです。
それでは実際に実験してみましょう。
図の２つの正方形を組み替えて、下の正方形を作ってみてください。
図形の中央付近でマウスの左ボタンをクリックし、ボタンを押しながら動かすと、図形を平行移動することができます。
下の 
ボタンをクリックしてマウスを動かすと、図形を回転することもできます。
ａ2＋ｂ2＝ｃ2 の関係を満たす３つの自然数ａ，ｂ，ｃはピタゴラス数といいます。
【問題２−１】（問題２−３を解く準備）
３，６，９・・のように３で割りきれる数を２乗した数は、当然３で割り切れます。
それでは、１，４，７・・のように３で割って１余る数を考えます。
これらの数を２乗した数１2，４2，７2・・を３で割った余りは何になるでしょうか。
【問題２−２】（問題２−３を解く準備）
２，５，８・・のように３で割って２余る数を考えます。
これらの数を２乗した数２2，５2，８2・・を３で割った余りは何になるでしょうか。
【問題２−３】
ａ，ｂ，ｃはピタゴラス数であるとします。
このときａ，ｂのうち、少なくとも一つは３で割り切れることを示してください。
【問題３−１】（高校生以上向き）
ａ，ｂ，ｃはピタゴラス数であるとするとき、
ａ×ｂは１２で割り切れることを示してください。
【問題３−２】（高校生以上向き）
ａ，ｂ，ｃはピタゴラス数であるとするとき、
ａ×ｂ×ｃは６０で割り切れることを示してください。
◆参考
三平方の定理の別の証明はこちらにあります。
解答用紙はこちらです。
| No. | 解答時刻 | 正解者 | |
| １ | 11/ 7 SUN 13:03 | 清川 育男 さん | 一般 |
| ２ | 11/ 7 SUN 15:09 | 緑川 正雄 さん | 一般 |
| ３ | 11/ 7 SUN 19:16 | 迷える羊 さん | 一般 |
| ４ | 11/ 7 SUN 21:41 | ゆうきリンリン さん | 中学３年 |
| ５ | 11/13 SAT 12:27 | 加藤 優彦 さん | 小学生 |
| ６ | 11/13 SAT 12:28 | AAAI さん | 大学生 |
◆過去問はこちらです。
◆ 今週の問題へ
数学の部屋へもどる。