◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
答え 6回
1つの手により 表1に示される数のグループに分類される。
これより、最善の場合は全部一致する1組を除いて残りが4等分される場合で、表2に示すように5回は試す必要がある。
一方、最悪の場合の平均的確率から見積もると6回程度となる。表3参照。
実際にこの辺をPCで探索すると、5回では無理で表4の手順により6回は可能であることが判った。
なお、6回の手順は他にもある。
表4において各夫婦は 0〜4で表わされ、最初は 01234 で試行する。
その結果5組一致なら終了。
N組一致なら表を下方に辿って、数値Nのところの右側の組を試行し、以下同様に試行する。
なおNへはリンクJumpである。
表4をプログラム化(JavaScript)した.HTMLを添付する。
| 表1 初手分類 | 表2 最善回数 | 表3 最悪平均確率 | |||||||
| 一致数 | 場合数 | 回数 | 120 | 回数 | 120 | ||||
| 0 | 44 | 1 | 45 | 1 | 45 | ||||
| 1 | 45 | 2 | 11 | 2 | 16.90 | ||||
| 2 | 20 | 3 | 3 | 3 | 6.40 | ||||
| 3 | 10 | 4 | 1 | 4 | 2.40 | ||||
| 4 | 0 | 5 | 完成 | 5 | 0.90 | ||||
| 5 | 1 | 6 | 6 | 完成 | |||||
| 合計 | 120 |
|
|
||||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 01234 | |||||
| 0 | 12340 | ||||
| 1へ | 0 | 34120 | |||
| 2へ | 1へ | 0 | 42310 | ||
| 3へ | 2へ | 0 | 23401 | ||
| 3へ | 1 | 20413 | |||
| 2 | 43012 | ||||
| 1 | 23041 | ||||
| 0 | 30412 | ||||
| 1 | 43102 | ||||
| 2 | 24013 | ||||
| 3 | 43021 | ||||
| 2 | 30421 | ||||
| 0 | 24103 | ||||
| 1 | 34012 | ||||
| 2 | 40123 | ||||
| 3 | 34102 | ||||
| 2 | 34021 | ||||
| 1 | 21340 | ||||
| 0 | 13420 | ||||
| 0 | 42013 | ||||
| 3 | 42103 | ||||
| 1 | 32401 | ||||
| 2 | 14023 | ||||
| 3 | 10423 | ||||
| 2 | 13402 | ||||
| 1 | 34120 | ||||
| 0 | 40312 | ||||
| 1 | 40321 | ||||
| 2 | 30142 | ||||
| 3 | 43120 | ||||
| 2 | 32140 | ||||
| 0 | 24301 | ||||
| 1 | 23041 | ||||
| 2 | 23410 | ||||
| 2 | 20143 | ||||
| 2 | 23140 | ||||
| 0 | 32410 | ||||
| 0 | 14302 | ||||
| 1 | 42301 | ||||
| 2 | 12403 | ||||
| 1 | 32041 | ||||
| 2 | 32410 | ||||
| 2 | 24310 | ||||
| 0 | 13042 | ||||
| 1 | 13420 | ||||
| 2 | 20341 | ||||
| 3 | 32140 | ||||
| 1 | 10342 | ||||
| 2 | 14320 | ||||
| 2 | 12043 | ||||
| 1 | 42310 | ||||
| 1 | 12340 | ||||
| 0 | 21340 | ||||
| 1へ | 0 | 43201 | |||
| 2へ | 0 | 30124 | |||
| 3へ | 2 | 04123 | |||
| 1 | 40132 | ||||
| 1 | 03412 | ||||
| 2 | 40213 | ||||
| 0 | 03421 | ||||
| 3 | 34201 | ||||
| 1 | 23140 | ||||
| 0 | 41023 | ||||
| 1 | 31402 | ||||
| 1 | 20431 | ||||
| 3 | 24031 | ||||
| 2 | 23014 | ||||
| 3 | 23104 | ||||
| 2 | 21403 | ||||
| 1 | 32140 | ||||
| 0 | 04132 | ||||
| 0 | 13024 | ||||
| 1 | 20314 | ||||
| 1 | 14203 | ||||
| 1 | 41302 | ||||
| 2 | 10432 | ||||
| 0 | 04321 | ||||
| 3 | 14032 | ||||
| 2 | 04312 | ||||
| 1 | 32410 | ||||
| 0 | 21043 | ||||
| 1 | 42031 | ||||
| 2 | 43210 | ||||
| 3 | 02413 | ||||
| 2 | 32014 | ||||
| 0 | 03142 | ||||
| 1 | 24130 | ||||
| 1 | 30241 | ||||
| 1 | 31420 | ||||
| 2 | 31042 | ||||
| 1 | 34210 | ||||
| 3 | 32104 | ||||
| 2 | 23140 | ||||
| 0 | 10324 | ||||
| 1 | 10243 | ||||
| 0 | 41320 | ||||
| 2 | 02143 | ||||
| 2 | 42130 | ||||
| 3 | 21340 | ||||
| 1 | 12304 | ||||
| 2 | 12430 | ||||
| 2 | 02341 | ||||
| 1 | 13240 | ||||
| 2 | 12340 | ||||
| 0 | 31240 | ||||
| 0 | 21430 | ||||
| 0 | 03124 | ||||
| 1 | 04132 | ||||
| 2 | 20134 | ||||
| 1 | 40231 | ||||
| 0 | 01423 | ||||
| 1 | 04213 | ||||
| 2 | 41032 | ||||
| 2 | 32410 | ||||
| 0 | 41203 | ||||
| 1 | 31024 | ||||
| 2 | 30214 | ||||
| 1 | 21340 | ||||
| 0 | 13204 | ||||
| 0 | 02431 | ||||
| 1 | 03241 | ||||
| 3 | 21304 | ||||
| 2 | 21430 | ||||
| 2 | 21340 | ||||
| 0 | 12034 | ||||
| 1 | 02314 | ||||
| 0 | 14230 | ||||
| 3 | 01342 | ||||
| 2 | 31240 | ||||
| 3 | 12340 | ||||
| 0 | 21340 | ||||
| 0 | 03214 | ||||
| 2 | 04231 | ||||
| 1 | 31204 | ||||
| 1 | 01432 | ||||
| 2 | 21034 | ||||
| 1 | 21340 | ||||
| 0 | 10234 | ||||
| 2 | 02134 | ||||
| 2 | 42310 | ||||
| 0 | 01243 | ||||
| 1 | 01324 | ||||
| 2 | 41230 |
◆出題者の山梨県 Footmark さんからのコメント。
みごと正解です。
最悪の場合でも5回までで正解の並び方が判明して、6回目で5組一致します。
証明できませんが、これが最善のようです。
◆山梨県 Footmark さんからの解答。
【追加問題1】
M(N,0) はN個の乱列の数に当たりますから、包除原理より次式が得られます。
M(N,0)
| =N!−NC1(Nー1)!+NC2(Nー2)!+…+(−1)NNCN(N−N)! |
| =N!{1− | 1 1! | + | 1 2! | − | 1 3! | +…+(−1)N | 1 N! | } |
M(N,1) は、1箇所一致はN箇所あり、
その各々の一致箇所に対して(Nー1)個の乱列の数になるので、
M(N,1)
=N{M(N−1,0)}
| =N!{1− | 1 1! | + | 1 2! | − | 1 3! | +…+(−1)N-1 | 1 (N−1)! | } |
∴ |M(N,0)−M(N,1)|=|(−1)N|=1
[補足]
数列 1,2,3,… の並び替えで、どの数も元の位置にない数列を乱列(derangement)と呼びます。
【追加問題2】
【追加問題1】より
M(N,0)
| =N!{1− | 1 1! | + | 1 2! | − | 1 3! | +…+(−1)N | 1 N! | } |
ですから、
| M(N,0) N! |
| =1− | 1 1! | + | 1 2! | − | 1 3! | +…+(−1)N | 1 N! |
∴ n→∞のとき
| M(N,0) N! | =e-1≒0.37 |
(ただし,eは自然対数の底)
◆愛知県 Y.M.Ojisan さんからのコメントと解答。
【追加問題1,2コメント】
正解です。【追加問題3解答】

一致組数の最大値で分類すると 最大5組 最大3組 最大2組 最大1組 の4種ある。
かならず合計5組だから 最大0組はありえない。
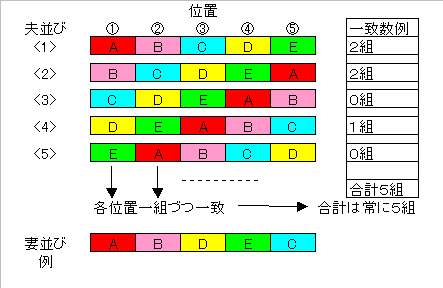
(あ)最大5組の場合
一致組数円順列は 0 0 5 0 0 しかなく、対称である。
(い)最大3組の場合
(う)最大2組の場合
個数5の円順列で考えるので、一致している最大2組が 夫並びの
<1>〜<5>のどれかにおいて (1)(2)か(1)(3)位置であると限定しても一般性を失わない。
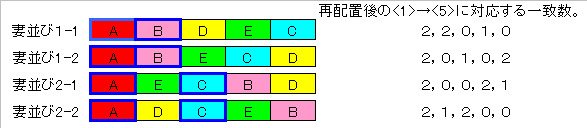
一方、残り3組は一致していない条件より、2タイプに限られる
これら 2×2=4ケースを実際に調べると (下図参照)一致組数円順列は
0 2 1 2 0 か 2 0 1 0 2
であり、対称である。
なお、下図においてはA−Eを再命名し、夫並びを2組一致した場合が先頭になるように回転して考えている。
(え)最大1組の場合
一致組数円順列は 1 1 1 1 1 しかなく、対称である。
以上より一致組数円順列は右左回り対称である。
【追加問題4解答】
答え n≦5
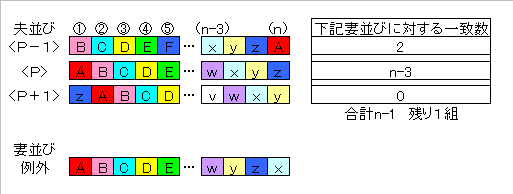
∵下図のようにn≧6では 「妻並び例外」に対して
夫並び<P>は[n−3]組一致し、2より大きいので単独最大値で対称中心である。
一方<P−1>と<P+1>の一致組数は0と2で等しくない。
よって、n≧6では例外が必ず存在し成立しない。
n=5は追加問題3で成立証明済み。
n=4は追加問題3の(あ)(い)(え)と同様の方法で成立が証明される。
n=3は追加問題3の(あ)(え)と同様の方法で成立が証明される。
n=2,1は明らかに成立する。
◆出題者の山梨県 Footmark さんからのコメント。
【追加問題3】,【追加問題4】とも、正解です。
5組までの時は対称になるのに、6組以上では対称になりません。
元の問題の解を得るのに、私はその対称性を利用しました。