仧幁帣搰導丂偲傕傂傠 偝傫偐傜偺夝摎
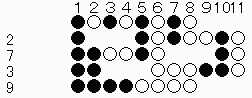
亂栤戣侾亃
亂夝亃係夞 (2仺7仺3仺9)

亂栤戣俀亃
亂夝亃俆夞 (4仺10仺3仺8仺1)

亂栤戣俁亃
亂夝亃俈夞 (6仺12仺8仺2仺11仺6仺1)
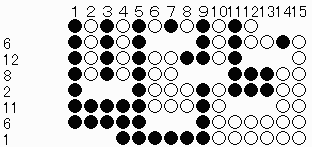
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
亂栤戣侾亃
2仺7仺3仺9
係庤
亂栤戣俀亃
4仺10仺3仺8仺1
俆庤偱壜擻偱偟偨丅
亂栤戣俁亃
2 5 11 3 12 6 1 2 7 1 12 8 3 13 2 7 11 3 12 6 13 2 7 12 1 6 11 1 2 7 12 1 11 6 1 2 7 13 3 8 12 1 2 9 4 12 3 8 1 2 9 12 4 11 8 1 2 9 13 3 7 11 1 3 8 13 2 7 12 1 3 12 9 5 11 2 13 4 7 3 12 2 9 1 4 7 11 2 12 5 13 4 9 13 2 6 11 1 4 12 3 10 6 9 1 4 12 8 11 3 9 1 5 10 1 12 8 3 13 5 10 4 9 2 12 1 5 12 1 11 7 3 13 6 1 8 12 2 10 13 6 1 10 5 12 2 13 6 3 7 11 2 5 13 6 11 4 9 2 13 1 6 12 8 2 11 6 1 7 2 13 3 8 12 1 7 12 1 11 6 2 13 8 1 4 9 2 12 1 8 3 13 2 7 12 1 8 11 6 2 12 6 13 8 11 6 12 2 6 13 9 2 13 3 7 11 1 9 4 10 5 12 2 13 9 4 13 2 6 11 1 10 1 9 3 11 5 13俈庤偱壜擻偱偟偨丅
亂栤戣係亃
仠俁恖偢偮偺帪丄
抝彈抝彈抝彈仩仩仩
抝仩仩仩抝彈彈抝彈
抝彈彈抝抝仩仩仩彈
仩仩仩抝抝抝彈彈彈
俁庤
仠俈恖偢偮偺帪丄
抝彈抝彈抝彈抝彈抝彈抝彈抝彈仩仩仩 抝彈抝彈抝仩仩仩抝彈抝彈抝彈彈抝彈 抝彈抝彈抝彈彈抝抝彈抝彈抝仩仩仩彈 抝彈抝彈仩仩仩抝抝彈抝彈抝抝彈彈彈 抝彈抝彈彈抝抝抝抝彈抝仩仩仩彈彈彈 抝彈仩仩仩抝抝抝抝彈抝抝彈彈彈彈彈 抝彈彈抝抝抝抝抝抝仩仩仩彈彈彈彈彈 仩仩仩抝抝抝抝抝抝抝彈彈彈彈彈彈彈俈庤偱壜擻偱偟偨丅
仠俋恖偢偮偺帪丄
抝彈抝彈抝彈抝彈抝彈抝彈抝彈抝彈抝彈仩仩仩 抝彈抝彈抝彈抝仩仩仩抝彈抝彈抝彈抝彈彈抝彈 抝彈抝彈抝彈抝彈彈抝抝彈抝彈抝彈抝仩仩仩彈 抝彈抝彈抝彈仩仩仩抝抝彈抝彈抝彈抝抝彈彈彈 抝彈抝彈抝彈彈抝抝抝抝彈抝彈抝仩仩仩彈彈彈 抝彈抝彈仩仩仩抝抝抝抝彈抝彈抝抝彈彈彈彈彈 抝彈抝彈彈抝抝抝抝抝抝彈抝仩仩仩彈彈彈彈彈 抝彈仩仩仩抝抝抝抝抝抝彈抝抝彈彈彈彈彈彈彈 抝彈彈抝抝抝抝抝抝抝抝仩仩仩彈彈彈彈彈彈彈 仩仩仩抝抝抝抝抝抝抝抝抝彈彈彈彈彈彈彈彈彈
| 抝彈偺恖悢 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 |
| 嵟彮庤悢 | 俁 | 係 | 俆 | 俈 | 俈 | 俋 | 俋 |
抝彈偦傟偧傟俶恖偢偮偲偡傞偲偒丄
俶偑婏悢偺偲偒偼俶庤丅
俶偑嬼悢偺偲偒
俶亖係偱偼 係庤丄
偦傟埲奜偼乮俶亄侾乯庤偑梊憐偝傟傑偡丅丂
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣侾亃
嵟彫庤悢丂係夞
2 仺 7 仺 3 仺 9丂偺傒
亂栤戣俀亃
嵟彫庤悢丂俆夞
4 仺 10 仺 3 仺 8 仺 1丂偺傒
亂栤戣俁亃
嵟彫庤悢丂俈夞
6 仺 11 仺 4 仺 9 仺 2仺 13 仺 1
丂塃婑偣丂愒惵
9 仺 4 仺10 仺 5 仺 12仺 2 仺13
丂嵍婑偣丂惵愒
2 仺 5 仺11 仺 3 仺 12仺 6 仺 1
丂塃婑偣丂惵愒
2 仺 7 仺 1 仺12 仺 8 仺 3 仺13
丂嵍婑偣丂愒惵
摍
亂栤戣係亃
嵟彫庤悢
俶偑俁丄係丄偍傛傃丂俆埲忋偺婏悢偺帪
丂俶夞偱偐偮侾庬偩偗
俶偑俇埲忋偺嬼悢偺帪
丂俶亄侾夞偱夝偺悢偼
丂俶亖俇丂丂俁係庬
丂俶亖俉丂丂侾俁俋庬
丂俶亖侾侽丂侾俁俋侽庬
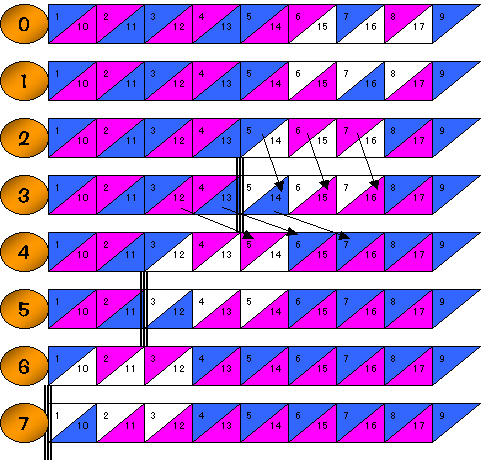
亂俁埲忋偺婏悢偺偲偒偺曽朄亃
庤弴丗N-1丂仺 2N 仺 N-2 仺 2N-2 仺 N-4仺 2N-4 仺 N-6 仺 丂丒丒丒俀慻偢偮丄 2偢偮尭彮丂丒丒丒 丂仺 3 仺 N+3 仺 1懄偪丄僙儖偺拞墰乮俶亄俀斣乯傪屌掕偟丆
(1)忋偺抜偐傜偦偺傑傑壓偵堏摦
(2)壓偺抜偺侾屄慜偐傜忋偺抜偵堏摦
(3)忋偺抜偐傜偦偺傑傑壓偵堏摦
(4)壓偺抜偺俀屄慜偐傜忋偺抜偵堏摦
埲屻(3)(4)傪孞傝曉偡丅
壓恾乮俶亖俈偺応崌乯嶲徠
側偍丄偙偺曽朄偑桞堦偺曽朄偱偁傞丅
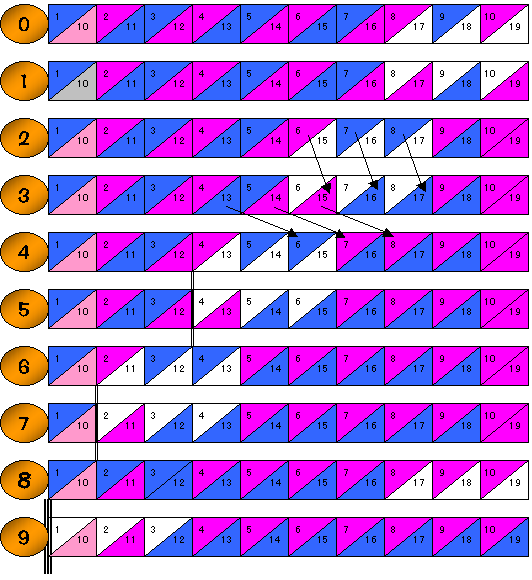
亂俇埲忋偺嬼悢偺偲偒偺曽朄亃
庤弴丗N 仺 2N-1 仺 N-2 仺 2N-3 仺 N-4仺 2N-5 仺 N-6 仺 丂丒丒丒俀慻偢偮丄 2偢偮尭彮丂N-2夞(庤=2)傑偱 丂仺 2N+1 仺 1懄偪丆丂僙儖偺拞墰乮俶亄俀斣乯傑偱側傜傋傞丅
(1)忋偺抜偐傜偦偺傑傑壓偵堏摦
(2)壓偺抜偺俀屄慜偐傜忋偺抜偵堏摦偡傞丅
埲屻(1)(2)傪俶亅侾夞傑偱孞傝曉偡丅
(3)俶夞栚偼丂俀N亄侾斣偐傜堏摦
(4)俶亄侾夞栚偼侾斣偐傜堏摦偡傞丅
壓恾乮俶亖俉偺応崌乯嶲徠丅
亂徹柧亃
仠俶偑婏悢偺偲偒丅
抝抝丂彈彈摨巑偑丂椬愙偟偰偄傞忬懺乮椬愙娭學偲偡傞乯悢偑
嵟弶乽侽乿偺忬懺偐傜嵟屻偼俀俶亅俀偵傑偱憹壛傪梫偡丅
堦曽丄堦搙偺堏摦偱怴偨側椬愙娭學偼嵟戝俀偱偁傞丅
傑偨丄堦斣嵟弶偼丄寗娫偑柍偄偺偱怴偨側椬愙娭學偼嵟戝侾偱偁傞丅
傛偭偰丂庤悢仏俀亅侾亞俀俶亅俀偱側偗傟偽側傜偢丄俶偼惍悢側偺偱庤悢偺嵟彫抣偼俶傛傝戝偒偄偐摍偟偄丅
慜偵帵偟偨傛偆偵丄幚嵺偵庤悢俶偺曽朄偑懚嵼偟偰偍傝丄廬偭偰丆庤悢嵟彫偼俶偱偁傞丅
仠俶偑嬼悢偺偲偒N亄侾偑嵟彫丂偍傛傃丂俶偑婏悢偺偲偒夝偑侾庬偩偗偺徹柧
乮侾乯娭楢栤戣偺愝掕
婎杮揑偵摨偠栤戣偱丄塃抂偲嵍抂傪偮側偄偱儖乕僾偝偣丄偡偙偟忦審偺備傞偄応崌傪峫偊傞丅
偦偟偰丄忦審傪娚偔偟偰傕懚嵼偟側偄偙偲傪徹柧偡傞丅
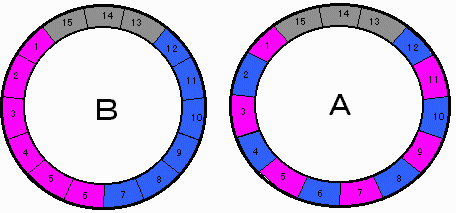
偡側傢偪丄恾偺俙偺忬懺偐傜椬愙偡傞俁恖偢偮傪曽岦傪曄偊側偄偱丄嬻偒僗儁乕僗偵堏摦偟側偑傜丄俛偺忬懺偵壗庤偱偱偒傞偐偲偄偆栤戣偱偁傞丅
側偍丄嵟屻偵慡懱傪夞揮偝偣偨傝丄棤曉偟偨傝偟偰傕傛偔丄偙傟偼庤悢偵悢偊側偄丅
愭偵偙偺栤戣偺摎偊傪尵偆偲丄嵟彮庤悢偼丂俶偱偁偭偰丄偦傟傜偼
丂棤曉偟亄抝偲彈傪岎姺偟偨傜摨偠庤弴偵側傞傕偺偲丄嵟弶偺庤偵昁偢偁傞俀庤偱暘椶偡傞偲俁孮偺傒偱偁傞丅
媡偵偄偆偲丂慡晹偱俀亊俀亊俁亖侾俀庬椶偑懚嵼偡傞丅
偙傟傜侾俀庬椶傪嬦枴偡傞偲丄婎杮栤戣偵揔崌偡傞傕偺偼俶偑婏悢偺偲偒偼偨偩侾偮丄俶偑嬼悢偺偲偒偼侽偱偁傞偙偲偑傢偐傞丅
扐偟俶亜俆
傛偭偰丄俶偑嬼悢偺偲偒偺嵟彫庤悢偼俶亄侾偱偁傞丅
徹柧偼椬愙娭學偺悢傪儀乕僗偵偍偙側偆丅
傑偨丄俙偐傜俛偺庤弴偺曄傢傝偵俛偐傜俙偺庤弴傪扵嶕偡傞丅
偙傟傜偼摨抣偱偁傞丅
偙偺応崌偺嵟屻偺庤偼椬愙娭學傪侾偺傒尭彮壜擻偱偁傞丅
側偤側傜丆恾俙偵偍偗傞丂13,14,15偺椬愙僙儖偑抝偲彈偱偁傝丄堦曽偦偙偵偁偭偨娭學偼乽抝彈抝乿偐乽彈抝彈乿偱側偗傟偽側傜側偄偺偱丄椬愙娭學悢偼侾偺傒偱偁傞偐傜偱偁傞丅
俶夞偱俛偐傜俙偵摓払偡傞偵偼椬愙娭學偺悢偺尭彮悢偼丄嵟屻偑侾夞偵寛傑偭偰偄傞偺偱丄
巆傝丂俶亅侾夞偺偆偪偺侾夞偩偗偑侾尭彮偟丄偦偺懠偱偼昁偢俀尭彮偡傞昁梫偑偁傞丅
乮俀乯椬愙娭學偺尭彮偑
俀仺俀仺俀丂丒丒丒丒丒丒俀仺侾仺侾丂偺応崌
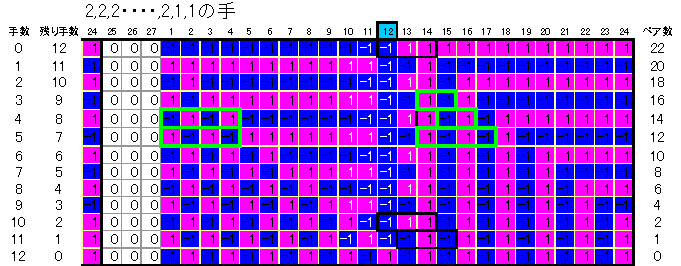
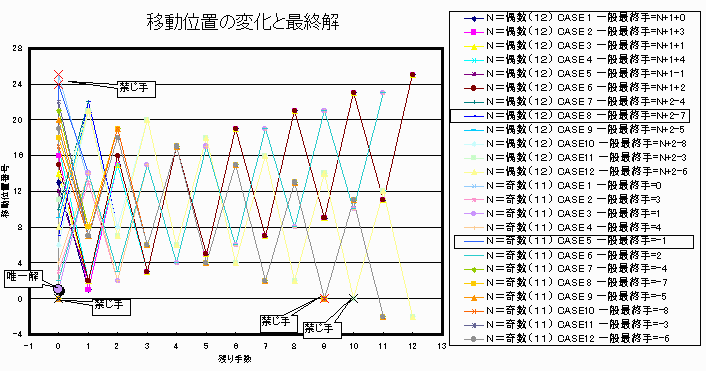
丂忋恾偼N=侾俀偺応崌傪帵偟偰偄傞偑丄堦斒偵椬愙娭學偑偢偭偲俀偢偮尭彮偡傞庤弴偼丄
堦斣嵟弶偑丂N亅侾偲N偺庤乮敀暥帤偲崟榞乯偺俀庤偺傒偱偁傞丅
偙傟傜偼嬀憸懳徧偺娭學偵偁傞偺偱丄N-1偺応崌偺傒傪峫偊傟偽傛偄丅
偦偺屻偺庤弴偼堏摦偟偨俁恖偺椉抂偑忢偵堎惈偱柍偗傟偽側傜偢偐偮椉抂偼椬愙偟偰偄傞昁梫偑偁傞偺偱忢偵侾捠傝乮敀暥帤乯偟偐側偔丆嬻偒僗儁乕僗傪忢偵愭摢偵夞揮偝偣傞偲丄恾偺傛偆偵僔儞儊僩儕僢僋偵曄壔偟偰備偔丅
丂嵟廔揑偵巆傝俀庤偺偲偙傠偱丄椬愙娭學傪俀尭彮偝偣傞偙偲偑弌棃側偔側傝丄侾偢偮尭彮偝偣傞庤弴偟偐側偔側傞丅
偙偺応崌丂敀暥帤丂偲丂崟榞偺俀庤偑偦傟偧傟偺抜奒偱偁傝丄崌寁俀孮丂係庬偑懚嵼偡傞丅
嵟弶偺嬀憸傪娷傔傞偲俉庬懚嵼偡傞丅丂
乮俁乯椬愙娭學偺尭彮偑
俀仺俀仺俀丂丒丒丒丒丒丒俀仺侾仺俀仺侾丂偺応崌

巆傝俁庤偺偲偙傠偱丄椬愙娭學傪侾尭偠傞庤弴偼丂抝傑偼偨彈偺俆楢懕偑側偄偺偱丄塃偑抝偱嵍偑彈偐偮堦曽偑椬愙娭學偵側偄偲偙傠堏摦偟側偗傟偽側傜側偄丅
廬偭偰丄堦斒偵忋恾偺敀暥帤偺庤丂侾孮偟偐側偔丄嵟廔庤偺俀庬乮敀暥帤偲崟榞乯偲嬀憸娭學傪妡偗偰係庬懚嵼偡傞丅
乮係乯椬愙娭學偺尭彮偑
俀仺俀仺俀丂丒丒丒丒丒丒俀仺侾仺俀仺俀仺侾丂偺応崌
偙偺応崌偼丄抝彈偑岎屳偵側傜傫偱偄傞晹暘偼丄傕偼傗摦偐偡偙偲偑弌棃側偄乮椬愙娭學偑側偄乯偺偱丄揔摉側N偱懚嵼偟側偗傟偽偦傟傛傝戝偒偄N偱偼懚嵼偟側偄丅
幚嵺丄N=6偺帪懚嵼偟側偄偙偲偑寁嶼婡偵傛傝妋偐傔傜傟偰偄傞偺偱丄偙偺庤偼懚嵼偟側偄丅
乮俆乯丒丒丒丒丒丒侾丂丒丒丒丒仺俀仺俀仺俀仺侾乮堦斒乯偺応崌偺徹柧偺弨旛
徹柧偺慜偵庒姳弨旛傪偟偰偍偔丅
偡傋偰丂椬愙娭學傪堦搙侾尭偠偨屻偺俀偢偮尭彮偝偣側偗傟偽側傜側偄忦審壓偱偺応崌偲偡傞丅
側偍丄尵梩偺掕媊偲偟偰丄埲壓傪婯掕偡傞丏
乽堏摦拞怱乿偲偼堏摦偝偣傞俁恖偺拞怱偺恖偺埵抲偲偡傞丅
乽儂儌堏摦乿偲偼摨惈偺俁恖乮抝抝抝丂or 彈彈彈乯偑堏摦偡傞偙偲丅
乽僿僥儘堏摦乿偲偼丂抝彈抝丂or丂彈抝彈丂偑堏摦偡傞偙偲丅
乽儂儌堎惈偱偁傞乿偲偼丂抝抝抝偵懳偡傞彈彈彈偺娭學
乽僿僥儘堎惈偱偁傞乿偲偼丂抝彈抝偵懳偡傞彈抝彈偺娭學
乽憃曄堏摦乿偲偼丂椬愙娭學偑椉懁偱愗傟堏摦愭偱暅妶偣偢丂椬愙娭學偑俀尭偠傞堏摦偺偙偲丅
乽扨曄堏摦乿偲偼丂椬愙娭學偑椉懁偱愗傟堏摦愭偱侾屄暅妶偡傞偐丄曅懁偱愗傟傞偺傒偺丂椬愙娭學偑侾尭偠傞堏摦偺偙偲丅
摿偵屻幰傪乽弮扨曄堏摦乿偲偡傞丅
乽愗懼屻忬懺乿偲偼丂扨曄堏摦捈屻偺忬懺偺偙偲丅
乮俆亅侾乯堏摦偼昁偢儂儌憃曄堏摦偐僿僥儘憃曄堏摦偱側偗傟偽側傜側偄丅
佹乮俀乯偺恾偵帵偟偨傛偆偵丄椬愙娭學尭彮検偑嬼悢忬懺偱偼嬻偒僗儁乕僗偺椉懁偼堎惈偱偁傞偑丄扨曄堏摦屻偼嬻偒僗儁乕僗椉懁偼摨惈偵側傞丅
廬偭偰丄偦偺屻椬愙娭學傪俀偢偮尭彮偝偣傞偵偼堏摦偺椉抂偼摨惈偱側偗傟偽側傜側偄丅
乮俆亅俀乯恾嶲徠
乮俆亅俀乯堏摦偡傞俁恖偺抂偺惈偼侾庤枅偵擖傟懼傢傞丅
![]() 丂
丂
佹丂堏摦尦偱椬愙娭學傪俀愗偭偨偁偲丄堏摦愭偱椬愙娭學傪侾偮傕夞暅偟偰偼側傜偢丄忋恾偐傜柧傜偐丅
乮俆亅俁乯抝彈偑岎屳偵係恖埲忋楢懕偡傞偲偙傠偼傕偼傗摦偐偡偙偲偑偱偒側偄丅
廬偭偰丄偙偺恖偨偪傪娷傓堏摦偼偱偒側偄丅
![]()
佹丂忦審壓偱偼丄椬愙娭學偺柍偄嫬栚偱愗傞偙偲偼弌棃側偄偺偱丄忋恾偺堏摦拞怱偑亊偺埵抲偼棙梡偱偒側偄丅
廬偭偰偙傟傜係恖偼傕偼傗堏摦偱偒側偄丏
乮俆亅係乯摿偵僿僥儘憃曄堏摦乮墿怓榞乯屻偵偼丂壓恾偺傛偆偵丄俆恖偺晄摦忬懺偲俈屄偺堏摦晄壜偺堏摦拞怱偑偱偒傞丅
![]()
乮俆亅俆乯嬻敀晹偵椬愙偟偰抝彈偑岎屳偵俁恖楢懕偡傞偲偙傠偼傕偼傗摦偐偡偙偲偑偱偒側偄丅
廬偭偰丄偙偺恖偨偪傪娷傓堏摦偼偱偒側偄丅
![]()
佹丂忦審壓偱偼丄椬愙娭學偺柍偄嫬栚偱愗傞偙偲偼弌棃側偄偺偱丄忋恾偺堏摦拞怱偑亊偺埵抲偼棙梡偱偒側偄丅
偐偮嬻敀晹偑杽傑偭偨屻偺忬懺偱偼偐側傜偢岎屳偵昁偢係恖側傜傇偺偱丄
乮俆亅俁乯偵傛傝偙傟傜弶婜偺俁恖偼堏摦偱偒側偄丏
乮俆亅俇乯儂儌憃曄堏摦壜擻側恖偼丂愗懼屻忬懺偐傜枹堏摦偺恖偵尷傜傟傞丅
廬偭偰丆俵恖偑摨惈偱楢懕偟偰偄傞忬懺偐傜偼儂儌堏摦偼
嵟戝偱傕乵(俵-侾)/4乶慻偩偗偱偁傞丅
偙偙偱 [ ] 偼僈僂僗婰崋丅壓恾嶲徠
![]()
佹儂儌堏摦偡傞偵偼嵟掅俆恖偑摨惈偱楢懕偟偰偄側偗傟偽側傜側偄偑丆堏摦屻偵偼楢懕偱偒傞偺偼嵟戝偱傕俁恖偱偁傞偐傜偱偁傞丅
乮俆亅俈乯巆傝俀庤忬懺偵墬偄偰傊僥儘憃曄堏摦嵪傒偺拞怱側偄偟嬻敀僗儁乕僗拞怱偺娫妘偼
捠忢偼乮俆亅係乯偵傛傝嵟彫係偱偁傞偑丄堦売強偩偗偼摨惈傊僥儘憃曄堏摦屻拞怱側偄偟嬻敀僗儁乕僗娫偱俉埲忋偱偁傞丅

佹丂巆傝俀庤偺忬懺傪媡偐傜偨偳傞偲忋偺恾偺忬懺偱偁傞丅
廬偭偰丄巆傝俀庤偵偍偗傞嵟屻偺僿僥儘堏摦偺椉懁偼丄摨惈偺僿僥儘憃曄堏摦乮墿怓榞乯側偄偟嬻敀僗儁乕僗偺応崌丄嵟彫偱傕娫妘偼俉昁梫偱偁傞丅
偝傜偵堎惈傊僥儘側傜俋昁梫偱偁傞丅
乮俇乯丒丒丒丒丒丒侾丂丒丒丒丒仺俀仺俀仺俀仺侾乮堦斒乯偺応崌偺徹柧
乮俇亅侾乯丂弶庤偑扨曄堏摦丂搑拞偼慡晹憃曄堏摦丄嵟屻偑弮扨曄堏摦偺応崌
乮俀乯偺庤悢侽偺忬懺偐傜丄扨曄堏摦偟偨屻偺忬懺偼丂
俶亞俆偺偲偒丂惈偺岎姺偼摨偠偲偡傞偲丄堦斒偵壓婰僷僞乕儞偺傒偱偁傞丅
側偍倠偼摨惈偑倠恖楢懕傪堄枴偡傞丅
傑偨乮丂乯撪偼乮俀乯偺恾偵懳墳偡傞丂
俶亖侾俀偺応崌偺抣偱偁傞丅
![]()
偙偺忬懺偐傜丄巆傝庤悢俀偺忬懺峫偊傞丅
乮俆亅俇乯偺曗戣傪梡偄傞偺偱丄俶傪係傪朄偲偟偰暘椶偟丄乮俆乯偺曗戣傪梡偄傞偲壓昞偲側傞丅
摿偵丂俹崁傪愢柧偡傞丅丂
乮俆亅俈乯偵傛傝憃曄傊僥儘堏摦偺嵟弶偺庤偱俈僙儖偑堏摦拞怱偐傜彍奜偝傟丄
埲屻乮俆亅俇乯偵傛傝憃曄傊僥儘堏摦侾夞偵偮偒係僙儖偑彍奜偝傟傞偲偲傕偵丄
俬崁偑侾埲忋側傜
乮俆亅俇乯偵傛傝亄係僙儖偑彍奜偝傟傞丅
傑偨嬻敀僗儁乕僗偼侾屄偺憃曄傊僥儘堏摦屻偲摨偠岠壥傪傕偮偺偱丂
搒崌丂俈亄係仏乮俬亄侾乯僙儖偑堏摦拞怱偱偄傞偙偲偑弌棃側偔側傞丅
丂寢壥丄巆傝俀庤偵偍偗傞丄憃曄堏摦偱偒傞僙儖偺悢Q崁偼嵟戝偱傕
俶亖俇丆侾侽丆侾係丏丅丅丅偺応崌偺侽偲側傝丄偙偺傛偆側堏摦偼晄壜擻偱偁傞偙偲偑傢偐傞丅
側偍丄俰崁俴崁偼嶲峫偱偁傝徹柧偵偼晄梫丅
|
婰崋 |
N丂 |
C |
D |
E |
F |
G |
H |
I |
J |
L |
俹 |
俻 |
|
崁栚 |
N椺 |
type# |
僙儖悢 |
巆傝庤悢俀傑偱偺 |
抝偺嵟戝 |
彈偺嵟戝 |
憃曄 |
憃曄 |
椉抂抝偺 |
椉抂彈偺 |
堏摦晄壜拞怱僙儖偺悢 |
堏摦壜擻 |
|
幃 |
丂 |
N mod 4 |
俀俶亄俁 |
N-3 |
[(N-1)/4] |
[(N-2)/4] |
F+G |
俤亅俫 |
[(E+1)/2]-F |
[E/2]-G |
俈+4*(I+侾) |
D-P |
|
type0 |
12 |
0 |
27 |
9 |
2 |
2 |
4 |
5 |
3 |
2 |
31 |
-4 |
|
type1 |
9 |
1 |
21 |
6 |
2 |
1 |
3 |
3 |
1 |
2 |
23 |
-2 |
|
type2 |
6 |
2 |
15 |
3 |
1 |
1 |
2 |
1 |
1 |
0 |
15 |
0 |
|
type3 |
7 |
3 |
17 |
4 |
1 |
1 |
2 |
2 |
1 |
1 |
19 |
-2 |
乮俇亅俀乯
弶庤偑憃曄堏摦丂俀庤栚偑扨曄堏摦丂丄搑拞偼慡晹憃曄堏摦丄嵟屻偑弮扨曄堏摦偺応崌丂
乮俀乯偺庤悢侾偺忬懺偐傜丄扨曄堏摦偟偨屻偺忬懺偼
俶亞俇偺偲偒丂惈偺岎姺傪摨偠偲偡傞偲丄堦斒偵壓婰俁僷僞乕儞偺傒偱偁傞丅
傑偨乮丂乯撪偼乮俀乯偺恾偵懳墳偡傞丂俶亖侾俀偺応崌偺抣偱偁傞丅

(1)偺応崌偼墿怓榞偺係恖偑乮俆亅俁乯偵傛傝堏摦偱偒側偄偺偱丄
N偑俀彫偝偄応崌偺乮俇亅侾乯偺働乕僗偵娷傑傟丄晄壜擻偱偁傞丅
(2)(3)偺応崌傪乮俇亅侾乯偲摨偠曽朄偱専嵏偡傞偲埲壓偱偁傞丅
傛偭偰丄壜擻惈偑偁傞偺偼丂
(2)type3丂N=俈亄4m偺応崌偺傒丅
|
2122(2) |
||||||||||||
|
婰崋 |
N丂 |
C |
D |
E |
F |
G |
H |
I |
J |
L |
俹 |
俻 |
|
崁栚 |
N椺 |
type# |
僙儖悢 |
巆傝庤悢俀傑偱偺庤悢 |
抝偺嵟戝憃曄儂儌堏摦悢 |
彈偺嵟戝憃曄儂儌堏摦悢 |
憃曄儂儌堏摦嵟戝悢 |
憃曄傊僥儘堏摦嵟彫悢 |
椉抂抝偺嵟戝憃曄傊僥儘堏摦悢 |
椉抂彈偺嵟戝憃曄傊僥儘堏摦悢 |
堏摦晄壜拞怱僙儖偺悢 @N亜6 |
堏摦壜擻拞怱悢 |
|
幃 |
N mod 4 |
俀俶亄俁 |
N-4 |
[(N-3)/4] |
[(N-3)/4] |
F+G |
俤亅俫 |
[(E+1)/2]-F |
[E/2]-G |
3+4*(I+2) |
D-P |
|
|
type0 |
12 |
0 |
27 |
8 |
2 |
2 |
4 |
4 |
2 |
2 |
27 |
0 |
|
type1 |
9 |
1 |
21 |
5 |
1 |
1 |
2 |
3 |
2 |
1 |
23 |
-2 |
|
type2 |
10 |
2 |
23 |
6 |
1 |
1 |
2 |
4 |
2 |
2 |
27 |
-4 |
|
type3 |
7 |
3 |
17 |
3 |
1 |
1 |
2 |
1 |
1 |
0 |
15 |
2 |
type3偑晄壜擻偱偁傞偙偲偼乮俇亅俆乯偱徹柧偡傞丅
|
2122(3) |
||||||||||||
|
婰崋 |
N丂 |
C |
D |
E |
F |
G |
H |
I |
J |
L |
俹 |
俻 |
|
崁栚 |
N椺 |
type# |
僙儖悢 |
巆傝庤悢俀傑偱偺庤悢 |
抝偺嵟戝憃曄儂儌堏摦悢 |
彈偺嵟戝憃曄儂儌堏摦悢 |
憃曄儂儌堏摦嵟戝悢 |
憃曄傊僥儘堏摦嵟彫悢 |
椉抂抝偺嵟戝憃曄傊僥儘堏摦悢 |
椉抂彈偺嵟戝憃曄傊僥儘堏摦悢 |
堏摦晄壜拞怱僙儖偺悢 @N亜6 |
堏摦壜擻拞怱悢 |
|
幃 |
N mod 4 |
俀俶亄俁 |
N-4 |
[(N-2)/4] |
[(N-4)/4] |
F+G |
俤亅俫 |
[(E+1)/2]-F |
[E/2]-G |
3+4*(I+2) |
D-P |
|
|
type0 |
12 |
0 |
27 |
8 |
2 |
2 |
4 |
4 |
2 |
2 |
27 |
0 |
|
type1 |
9 |
1 |
21 |
5 |
1 |
1 |
2 |
3 |
2 |
1 |
23 |
-2 |
|
type2 |
10 |
2 |
23 |
6 |
2 |
1 |
3 |
3 |
1 |
2 |
23 |
0 |
|
type3 |
7 |
3 |
17 |
3 |
1 |
0 |
1 |
2 |
1 |
1 |
19 |
-2 |
乮俇亅俁乯侾乣俀庤栚偑憃曄堏摦丂俁庤栚偑扨曄堏摦丂丄搑拞偼慡晹憃曄堏摦丄嵟屻偑弮扨曄堏摦偺応崌
乮俀乯偺庤悢俀偺忬懺偐傜丄扨曄堏摦偟偨屻偺忬懺偼
俶亞俇偺偲偒丂惈偺岎姺傪摨偠偲偡傞偲丄堦斒偵壓婰俆僷僞乕儞偺傒偱偁傞丅
偙偺偆偪丄(1)(3)(4)嘍偺僷僞乕儞偵偼乮俆亅俁乯偵傛傝偙傟埲忋堏摦偱偒側偄晹暘偑偁傝丄
壓恾偺墿怓榞晹暘傪彍奜偡傞偲N偑彫偝偄応崌偺乮俇亅俀乯偺働乕僗偺堦晹偵婣拝偱偒傞偺偱丄悢妛揑婣擺朄偵傛傝晄壜擻偱偁傞丅
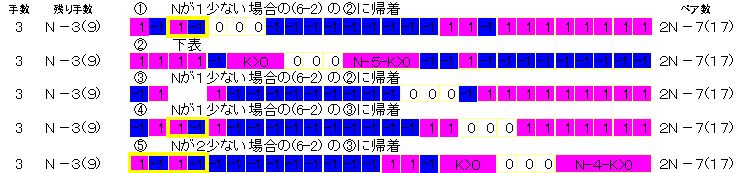 丂
丂
(2)偺応崌傪乮俇亅侾乯偲摨偠曽朄偱専嵏偡傞偲埲壓偱偁傞丅
傛偭偰丄杮働乕僗偼晄壜擻丅
|
2212 |
||||||||||||
|
婰崋 |
N丂 |
C |
D |
E |
F |
G |
H |
I |
J |
L |
俹 |
俻 |
|
崁栚 |
N椺 |
type# |
僙儖悢 |
巆傝庤悢俀傑偱偺庤悢 |
抝偺嵟戝憃曄儂儌堏摦悢 |
彈偺嵟戝憃曄儂儌堏摦悢 |
憃曄儂儌堏摦嵟戝悢 |
憃曄傊僥儘堏摦嵟彫悢 |
椉抂抝偺嵟戝憃曄傊僥儘堏摦悢 |
椉抂彈偺嵟戝憃曄傊僥儘堏摦悢 |
堏摦晄壜拞怱僙儖偺悢 @N亜6 |
堏摦壜擻拞怱悢 |
|
幃 |
N mod 4 |
俀俶亄俁 |
N-5 |
[(N-4)/4] |
[(N-7)/4] |
F+G |
俤亅俫 |
[(E+1)/2]-F |
[E/2]-G |
3+4*(I+2) |
D-P |
|
|
type0 |
12 |
0 |
27 |
7 |
2 |
1 |
3 |
4 |
2 |
2 |
27 |
0 |
|
type1 |
9 |
1 |
21 |
4 |
1 |
0 |
1 |
3 |
1 |
2 |
23 |
-2 |
|
type2 |
10 |
2 |
23 |
5 |
1 |
0 |
1 |
4 |
2 |
2 |
27 |
-4 |
|
type3 |
7 |
3 |
17 |
2 |
0 |
0 |
0 |
2 |
1 |
1 |
19 |
-2 |
乮俇亅係乯巒傔偺偆偪偑憃曄堏摦丂乮係埲忋乯庤栚偑扨曄堏摦丂丄搑拞偼慡晹憃曄堏摦丄嵟屻偑弮扨曄堏摦偺応崌
乮俀乯偺恾偺椢偺晹暘偑扨曄堏摦埲崀偱晄摦晹暘偵側傞丅
廬偭偰丄乮俀乯偺恾偱
(1)庤悢俁偺傕偺偼N偑侾彫偝偄応崌偺庤悢俀偺応崌偵
(2)庤悢係埲忋偺傕偺偼N偑俀彫偝偄応崌偺庤悢偑俀彮側偄傕偺応崌偵
婣拝偱偒丄悢妛揑婣擺朄偵傛傝晄壜擻偱偁傞丅
乮俇亅俆乯丂乮俇亅俀乯偺(2)偺俶亖俈亄係倣偺働乕僗
![]()
彈惈偵拲栚偡傞偲丂彈偺嵟戝憃曄儂儌堏摦悢偼丂
[(N-3)/4]=1+m=(N-3)/4 偱偁偭偰丄柍懯偑側偄丅
堦曽丄俻抣偼俀亝係偱偁偭偰丄僿僥儘憃曄堏摦偑堦偮憹偊偨傜丄惉棫偟側偔側傞丅
埲忋傛傝丄慡偰偺儂儌憃曄堏摦偼徚旓偟側偗傟偽側傜側偄丅
偙偺応崌儂儌堏摦偟偨嵍懁偺敳偗妅暘偵偼彈惈偺椬愙娭學偼懚嵼偣偢丄慡偰堏摦愭偺俁楢懕忬懺偺撪晹偺俀偙偢偮偵側傞丅
偙傟傜偼丄憃曄乮僿僥儘乯堏摦偱愗偭偰峴偔偟偐側偔丄廬偭偰丄儂儌堏摦愭偼係偲傃偵楢懕偟偰偄側偗傟偽側傜側偄丅
壓恾
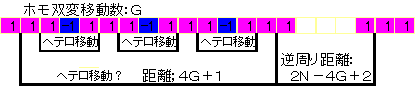
偙偺媡廃傝偺嫍棧傪俶亖俈亄係倣偵偮偄偰寁嶼偡傞偲丂
俀俶亅係俧亄俀亖侾係亄俉倣亅係倣亅係亄俀亖侾俀亄俉倣亜俁偱偁偭偰丄僿僥儘憃曄堏摦偡傞偙偲偑弌棃側偄丅
(俈乯傑偲傔
埲忋偐傜丄娭楢栤戣偱偁傞丂儕儞僌忬偺栤戣偱俶亞俇偺応崌偺庤悢偺嵟彫偼俶偱丄
慡偰侾俀庬椶懚嵼偡傞偙偲偑徹柧偱偒偨丅
側偍丄俶亞俇偺忦審偼庤悢俁埲壓偺晹暘偲巆傝庤悢俁埲壓偺晹暘偑廳側傜側偄偨傔偵昁梫側忦審偱偁傞丅
幚嵺丂寁嶼婡偱挷傋傞偲丄
俶亖俆偺応崌偼丂俶亞俇偺応崌偺奼挘偺侾俀庬埲奜偵係庬懚嵼偡傞丅
偡側傢偪侾俇庬丅
側偍丄俶亖係偺応崌偼丂侾係庬懚嵼丅
俶亖俁偺応崌偼俇庬偱偁偭偨丅
乮俉乯尦偺栤戣偺夝摎
儕儞僌偺栤戣傪尦偺栤戣偵曄偊傞偵偼埲壓偺忦審傪晅壛偡傟偽傛偄丅
乮俙乯儕儞僌偵摿桳偺丂俀俶亄俀乮俀俇乯丄俀俶亄俁乮俀俈乯偐傜偺堏摦傪嬛巭丅
乮俛乯嵟屻偵慡堳偮側偑傞偨傔偵丄庤悢偵娭學側偄斀揮丄夞揮傪偟側偄偲偒丄
嵟屻偺庤偑侾傑偨偼俀俶亄侾乮俀俆乯偱偁傞偙偲丅
侾俀庬椶偺曽朄偺偆偪乮俛乯傪枮懌偡傞偺偼丂俶偑婏悢側偄偟俇偺偲偒嵟屻偺庤偑侾偵側傞偨偩堦偮偱偁傝丄俶偑俉埲忋偺嬼悢偱偼懚嵼偟側偄丅
偙傟傜偵乮俙乯偺忦審傪壽偡偲丄俶偑婏悢偺応崌偼慡偰俷俲偱偁傞偑丄
俶亖俇偺働乕僗偼偙傟偵掞怗偡傞丅
傛偭偰丄俶亞俇偺偲偒丂俶偑嬼悢偺偲偒偺嵟彫庤悢偼俶偱偼側偄丅
傑偨丂俶偑婏悢偺偲偒偺嵟彫庤悢偼俶偱偁傝丄偦偺曽朄偼桞堦偱偁傞丅
埲忋
丂仧丂栤戣傊傕偳傞
丂仧丂崱廡偺栤戣傊
丂丂