◆石川県 迷える羊 さんからの解答
【問題1】
1月28日の午前0時には、この時計は4分30秒進んでいる。
これから12時間経つと、この時計は初めて5分進んでいることになる。
よって、1月28日の正午。
【問題2】
長針と秒針はそれぞれ、1時間に1回転と60回転する。
よって、長針と秒針が一直線になるのは、1時間に118回である。
2832【回/日】
短針と秒針はそれぞれ、12時間に1回転と720回転する。
よって、短針と秒針が1直線になるのは、12時間に1438回である。
2876【回/日】
短針と長針と秒針はそれぞれ、12時間に1回転と12回転と720回転する。
よって、3本が全て1直線になるのは、0時ちょうどと6時ちょうどの二回だけである。
4【回/日】
2832+2876−4=5704回
◆千葉県 緑川 正雄 さんからの解答
【問題1】
1月28日正午
1月29日午前8時
1月29日午後6時
1月30日午前4時
1月31日午前0時
【理由】
| 進んでいる時間 | 進んでいる時間 | ||
| 1月1日の 午前0時 | 0秒 | 正午 | 30秒 |
| 1月2日の 午前0時 | 10秒 | 正午 | 40秒 |
| 1月3日の 午前0時 | 20秒 | 正午 | 50秒 |
| 1月4日の 午前0時 | 30秒 | 正午 | 60秒 |
| 1月5日の 午前0時 | 40秒 | 正午 | 70秒 |
| : | : | : | : |
午前0時に5分(即ち300秒)進んでいる日をm日とすると
(m-1)×10=300よりm=31
この後時計は進み始め(最大30秒)、正午を境に遅れ始める(最大20秒)
よって、31日の午前0時以降の時計の進みかたは300秒よりも大きい。
正午に5分(即ち300秒)進んでいる日をn日とすると
(n+2)×10=300よりn=28
この前の12時間に時計は進んでいた。(最大30秒)
更に12時間前までには遅れていた。(最大20秒)
よって、28日の正午以前の時計の進みかたは300秒よりも小さい。
1月28日午前0時から1月31日正午までの時計の進みかたを整理すると
| 進んでいる時間 | 進んでいる時間 | ||
| 1月28日の 午前0時 | 270秒 | 正午 | 300秒 |
| 1月29日の 午前0時 | 280秒 | 正午 | 310秒 |
| 1月30日の 午前0時 | 290秒 | 正午 | 320秒 |
| 1月31日の 午前0時 | 300秒 |
以上より
1月28日正午
1月29日午前0時と正午の間
(300-280)÷30×12=8 午前8時
1月29日正午と1月30日午前0時の間
(310-300)÷20×12=6 午後6時
1月30日午前0時と正午の間
(300-290)÷30×12=4 午前4時
1月31日午前0時
が時計が5分進んでいる日時である。
【問題2】
5704回
【理由】
現時刻をh[時]とする。
0≦h<12で計算を行なう。
時、分、秒に換算しn時m分t秒であれば、
h=n+m/60+t/3600
(n:整数=0,1,2,....,10,11、m:整数=0,1,2,....,58,59、t:実数0≦t<60)
各々の針の時計回りの角度を求めると
時針は30×h =30×n+1/2×m+1/120×t
分針は360×h ≡6×m+1/10×t[mod360]
秒針は21600×h≡6×t [mod360]である。
この場合
0≦30×n+1/2×m+1/120×t,6×m+1/10×t,6×t<360となる。
時針と秒針が1直線に並ぶ回数は1438通りである。
(0≦h<12)
<理由>
(Case1)時針と秒針が重なるケース
30×n+1/2×m+1/120×t=6×t+360×p[pは整数]より、
(6-1/120)×t=30×n+1/2×m-360×p[pは整数]
(12-1/60)×t=60×n+m-720×p[pは整数] …(式1)
ところで
0≦(12-1/60)×t<719、60×n+m=0,1,..,719
であるから、
(式1)はp=0の時にのみ
0≦(12-1/60)×t=60×n+m<719
を満足するt=t(n,m)が
(n,m)= ( 0, 0)( 0, 1)( 0, 2)( 0, 3) ………………( 0,58)( 0,59) ( 1, 0)( 0, 1)( 1, 2)( 1, 3) ………………( 1,58)( 1,59) ( 2, 0)( 2, 1)( 0, 1)( 2, 3) ………………( 2,58)( 2,59) :::::::::::::::::: (10, 0)(10, 1)(10, 2)(10, 3) ………………(10,58)(10,59) (11, 0)(11, 1)(11, 2)(11, 3) ………………(11,58)の719の組み合せで存在し
t(n,m)=60/719×(60×n+m)………(1)
(Case2)時針と秒針が反対むきとなるケース
30×n+1/2×m+1/120×t=6×t+360×p-180[pは整数]より、
(12-1/60)×t=60×n+m+360-720×p[pは整数] …(式2)
ところで
0≦(12-1/60)×t<719、60×n+m=0,1,..,719である。
(Case2-1)p=0のとき
0≦(12-1/60)×t<719かつ360≦60×n+m+360<719より
360≦(12-1/60)×t=60×n+m+360<719
を満足するt=t(n,m)が
(n,m)= ( 0, 0)( 0, 1)( 0, 2)( 0, 3) ………………( 0,58)( 0,59) ( 1, 0)( 0, 1)( 1, 2)( 1, 3) ………………( 1,58)( 1,59) ( 2, 0)( 2, 1)( 0, 1)( 2, 3) ………………( 2,58)( 2,59) :::::::::::::::::: ( 5, 0)( 5, 1)( 5, 2)( 5, 3) ………………( 5,58)の359の組み合せでtが存在し
t(n,m)=60/719×(60×n+m+360)………(2)
(Case2-2)p=1のとき
0≦(12-1/60)×t<719かつ-360≦60×n+m-360<359より、
0≦(12-1/60)×t=60×n+m-360<359
を満足するt=t(n,m)が
(n,m)= ( 6, 0)( 6, 1)( 6, 2)( 6, 3) ………………( 6,58)( 6,59) :::::::::::::::::: (10, 0)(10, 1)(10, 2)(10, 3) ………………(10,58)(10,59) (11, 0)(11, 1)(11, 2)(11, 3) ………………(11,58)(11,59)の360の組み合せでtが存在し
t(n,m)=60/719×(60×n+m-360)………(3)
よって時針と秒針が反対むきとなるケースは
360+359=719(通り)である。
分針と秒針が1直線に並ぶ回数は1416通りである。
(0≦h<12)
<理由>
(Case1)分針と秒針が重なるケース
分針と秒針は0時台、1時台、…、11時台の各時間帯に
6×m+1/10×t=6×t-360×p[pは整数]
よって5.9×t=6×m+360×p[pは整数]
ところで
0≦5.9×t<354かつ0≦6×m<354であるから
p=0の時にのみ、m=0,1,...,58の59通りでtが存在し
t(m)=60/59×m………(4)
0≦h<12では12×59=708(回)分針と秒針が重なる。
(Case2)分針と秒針が反対むきとなるケース
分針と秒針は0時台、1時台、…、11時台の各時間帯に
6×m+1/10×t=6×t+180-360×p[pは整数]
よって5.9×t=6×m-180+360×p[pは整数]
ところで0≦5.9×t<354
かつ0≦6×m≦354である。
(Case2-1)p=1の時
0≦5.9×t<354かつ180≦6×m+180≦534より、
180≦5.9×t=6×m+180<354
よって
m=0,1,...,28の29通りについてtが存在し
t(m)=60/59×(6×m+180)………(5)
を得る。
(Case2-2)p=0の時
0≦5.9×t<354かつ-180≦6×m-180≦174より
0≦5.9×t=6×m-180≦174
よって
m=30,31,...,59の30通りについてtが存在し
t(m)=60/59×(6×m-180)………(6)
を得る。
0≦h<12では12×59=708(回)分針と秒針が反対むきとなる。
以上(Case1)(Case2)より分針と秒針は0≦h<12では
708+708=1416(回)反対むきとなる。
時針と分針と秒針が1直線に並ぶ回数は2通りである。
(0≦h<12)
<理由>
時針と秒針が1直線に並ぶ時間の単位[秒](t(n,m)の値)は
(1)、(2)、(3)のいずれかの式で表される。
及び
分針と秒針が1直線に並ぶ時間の単位[秒](t(m)の値)は
(4)、(5)、(6)のいずれかの式で表される。
(1)、(2)、(3)の分母は719であり、(4)、(5)、(6)の分母は59である。
719と59とは互いに素であるから、(1)、(2)、(3)のいずれかが(4)、(5)、(6)のいずれかに等しくなるためには、
t(n,m)=0かつt(m)=0でなくてはならない。
(1)、(2)、(3)でt(n,m)=0となる(n,m)を求める。
(1)より(n,m)=(0,0)の時t(n,m)=0…(7)
(3)より(n,m)=(6,0)の時t(n,m)=0…(8)
(4)、(5)、(6)でt(m)=0となるmを求める。
(4)よりm=0の時t(m)=0 …(9)
(6)よりm=30の時t(m)=0 …(10)
(7)と(9)を同時に満たす(n,m)は(n,m)=(0,0)だけである。
(7)と(10)を同時に満たす(n,m)は存在しない。
(8)と(9)を同時に満たす(n,m)は(n,m)=(6,0)だけである。
(8)と(10)を同時に満たす(n,m)は存在しない。
よって、0時0分と6時0分に時針と分針と秒針が1直線に並ぶ。
<結論>
以上より、秒針が時針、分針のどちらかと1直線に並ぶのは
0≦h<12で1438+1416-2=2852(回)あり、
1日に2852×2=5704(回)ある。
◆北海道 けんけん さんからの解答
【問題1】
この時計は午前午後あわせて24時間経つと10秒進む。
5分進むのは、初めて正午に5分以上進んでいる日である。
ここで、その日を1月X日とすると、
30+10(X−1)≧5×60
という式を立て、この解のうちの最小値が答えとなる。
これを解くと、X≧28
したがって、5分進むのは、「1月28日」である。
【問題2】
秒針は1時間に60周し、長針は1時間に1周することから、仮に秒針が次に長針と出会ったとき、1周したというふうに考えると、 秒針は1時間に59周するといえる。
すなわち、秒針と長針は1時間に
59×2=118(回)
1日に
118×24=2832(回) 一直線になる。
一方、秒針と短針は同様に考えると、
12時間に
719×2=1438(回)
1日に
1438×2=2876(回) 一直線になる。
これらの和から、秒針・長針・短針の3つが一直線になる回数を引けばよい。
3つが一直線になる回数は、
0:00、6:00、12:00、18:00 の4回である。
よって、求める回数は、
2832+2876−4=5704(回)
【おまけ1】
ある時計の中心を点C、短針の先端を点Aとする。
一般的に∠AOCは微小であるから、近似計算をすることとする。
ただし、θは上向きを正とする。
OA−OC=Δr とすれば、
Δrの合計が負(ΣΔr<0)となる場合が存在することを示せばよい。
∠AOC=θのとき、
Δr=AC×θ
たとえば、
ΣΔr=Σ(AC×θ)>0 ならば、
6時間後は、
∠AOC=−θ となっており、このとき
ΣΔr<0
よって示された。
【おまけ2】
ACの長さは大小さまざまである。
例えばACの長さの大きい複数の時計が
∠AOC>0の状態で止まっており、
恒常的にΣΔr>0となる場合がある。
しかし、止まっている時計のACの長さが小さく、そのような時計の数が少ないときは、その時計による影響は少なく、無視することができる。
時計それぞれの進み方や遅れ方がなめらかに、かつ連続的に変化する場合
(進み方、遅れ方が一定の場合を含む)
については、すべての時計が同時にある定められた初期状態に戻るときが必ずくる。
この間かかる時間を周期という。
一周期を経過するにあたっては、
必ずΣΔr<0となる時刻を通過しなければならないわけである。
また、動かなくなった時計がない場合は上で述べた条件の下では、
ΣΔr<0になる時刻が存在する。
◆東京都 小林 祐介 さんからの解答
【問題1】
午前0時の時点で時計が4分30秒進んでいる日は
270÷10=27より27日後
よって1月28日の午後0時にこの時計は5分進む。
答.1月28日
【問題2】
秒針が時針に追いついた瞬間から、次に追いつく直前までに時針と秒針は2回一直線上に並ぶ。
0時から24時までの間に
時針は2回転し、秒針は1440回転するので、
(1440−2)×2=2876
同様に、0時から24時までの間に
分針は24回転し、秒針は1440回転するので、
(1440−24)×2=2832
また、全ての針が一直線上に並ぶのは0時、6時、12時、18時の4回のみ。
よって求める答は
2876+2832−4=5704
答.5704回
【おまけ1・2】
![]() は関数xの全区間における平均値を表すものとする。
は関数xの全区間における平均値を表すものとする。
ある時計1について考えてみる。
時計1の店の中央からの距離をx1、
時計の直径をy1、
時計の短針と店の中央と時計の中心を結んだ直線とのなす角を
θ1とする。
このとき、
店の中央から短針の先端までの距離をz1とすると、
z12=x12+y12−2x1y1cosθ1
![]()
この時
z1'=x1−y1cosθ1(x1≧y1)
または
z1'=y1−x1cosθ1(x1<y1)
とおくと
(等号はθ1=nπ(nは整数)のとき成立)
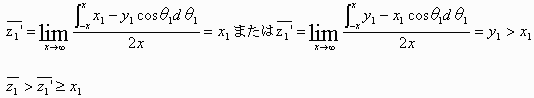
同様に時計2、3、…100についても
![]()
よって
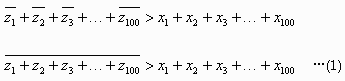
ここで点Oから時計の中心までの距離の和が、常に短針の先端までの距離の和よりも大きいか等しいとすると、
![]()
が成り立つ。よって
![]()
これは明らかに(1)に矛盾する。
よって点Oから時計の中心までの距離の和が、短針の先端までの距離の和よりも小さくなる時が存在する。
また、このことはそれぞれの時計が遅れていようが進んでいようが、一定のペースで動いている限り成り立つ。
◆ 問題へもどる
◆ 今週の問題へ