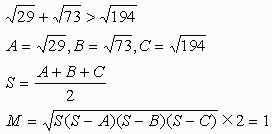
◆石川県 迷える羊 さんからの解答
【問題1】
赤と緑の四角形の境界線について考える。
将来5×13の長方形に並べたいのだから、境界線は上から5桝目の点から3桝目の点に斜めに引かれている。
よって、赤や緑の四角形の最も小さな角の大きさを、αとすると、
| tanα= |
5 ――― 2 |
青と黄色の三角形の境界線について考える。
青と黄色の三角形を合わせると、3×8の長方形になっていて、境界線はその長方形の対角線となっている。
よって、青や黄色の三角形の二番目に小さい角の大きさを、βとすると、
| tanβ= |
8 ――― 3 |
今、図より、
| 0<α,β< |
π ――― 2 | だから、 |
α<β
結論は、5×13の長方形に並べ替えようとした時に、斜めに対角線が入っている様に見える部分に隙間がある。
そしてその隙間の面積が1である。
【問題2】
(2,3,5),(13,21,34),
(34,55,89),(89,144,233),…
【問題3】
数学的帰納法により、式(ア)を証明する。
≪1≫n=2のとき、
F(3)=2、F(2)=F(1)=1 だから、
F(3)×F(1)−F(2)2=(−1)2
よって、式(ア)は成立する。
≪2≫n=kのとき、式(ア)が成立すると仮定すると、
【kは自然数、k>1】
式(ア)より、
F(k+1)×F(k-1)−F(k)2=(−1)k …(イ)
今、F(k+2)=F(k+1)+F(k)、
F(k+1)=F(k)+F(k-1)だから、
F(k+2)×F(k)−F(k+1)2
=F(k)2+F(k+1)×{F(k)−F(k+1)}
=−{F(k+1)×F(k-1)−F(k)2}
式(イ)を代入して、
F(k+2)×F(k)−F(k+1)2=(−1)k+1
よって、n=k+1のときも、式(ア)は成立する。
≪1≫,≪2≫より、式(ア)は、2以上の任意の自然数nについて成立する。
◆広島県 清川 育男 さんからの解答
【問題1】
赤色の図形と黄色の図形を組み合わせた図形は直角三角形にならない。
青色の図形と緑色の図形を組み合わせた図形は直角三角形にならない。
ピタゴラスの定理によると、それらの図形は凹型四角形になる。
4辺は5,13,SQR(73),SQR(29)となる。
向かい合った2辺がそれぞれSQR(73),SQR(29)の平行四辺形のすきまがある。
すきまの平行四辺形の面積は、ヘロンの公式によると、
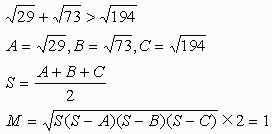
1増えた原因はすきまの平行四辺形の面積にある。
【問題2】
21×21の正方形 441
13×34の長方形 442にする。
【問題3】
フィボナッチの一般式を使って直接証明する。
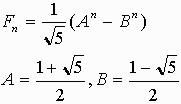
A*B=-1,A-B=
(Fn+1*Fn-1)-Fn2
=(1/5)*(An-1*Bn-1)*(2AB-A2-B2)
=(1/5)*(A*B)n-1*(-(A-B)2)
=(1/5)*(-1)n*5
=(-1)n
ひらめきのない計算問題になってしまいました。
◆千葉県 緑川 敦 さんからの解答
【問題1の回答】
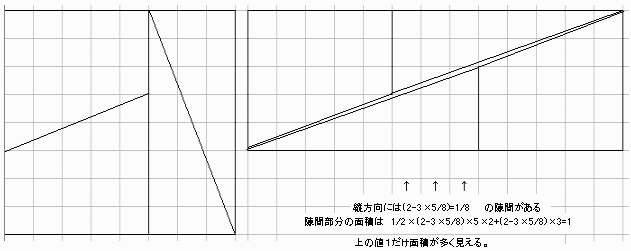
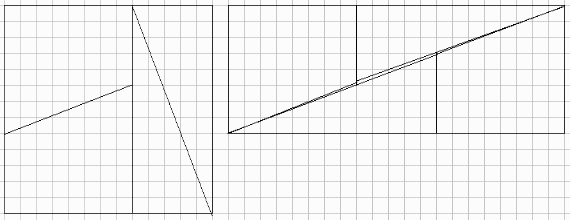
台形と3角形のタテのすきまがうまらない。
図表1の通り
◆千葉県 緑川 正雄 さんからの解答
【問題1の回答】
横13、縦5の状態では上の台形と三角形及び下の三角形と台形の間に、鉛直方向の隙間が出きる。
左上台形の長さ3の辺と左下三角形の左から水平方向5の点の高さの和は
| 5より(2-3× |
5 ―― 8 | )=1/8だけ短い。 |
右下台形の長さ3の辺と右上三角形の右から水平方向5の点の高さの和も同様に
| 5より(2-3× |
5 ―― 8 | )=1/8だけ短い。 |
隙間部分の面積は
|
1 ― 2 | ×(2-3× |
5 ― 8 | )×5×2+(2-3× |
5 ― 8 | )×3=1 |
横8、縦8の状態での面積より見かけ上、1大きく見える。
【問題2の回答】
(8,13,21)の組み合わせ
【問題3】
数学的帰納法により証明する。
n=2のとき
まずF(3)=F(1)+F(2)=2であるから
F(3)×F(1)-F(2)2
=2×12
=(-1)2
n=kの時に
F(K+1)×F(K-1)-F(K)2=(-1)k
が成立するものと仮定する。
n=k+1の時
F(K+2)×F(K)-F(K+1)2
={F(K)+F(K+1)}×F(K)-F(K+1)2 [定義より]
=F(K)2+F(K)×F(K+1)-F(K+1)2
=F(K)2+{F(K)-F(K+1)}×F(K+1)
=F(K)2+{-F(K-1)}×F(K+1) [定義より]
=-(-1)k [帰納法の仮定より]
=(-1)k+1
◆ 問題へもどる
◆ 今週の問題へ