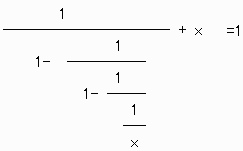
◆愛知県の中学校3年生 ゆうきリンリン さんからの解答
【問題1】
3桁の数Aを『100a+10b+c』とします。
これを逆順にした数Bは『100c+10b+a』です。
この2つの数の差、Cは『99a−99c』,
つまり『99(a−c)』となり、99の倍数ということが分かります。
a−cというのは、1桁です。
そして、『99×(2以上の1桁の整数)』というのは、
『198』『297』『396』『495』
『594』『693』『792』『891』の、8つです。
この8つの整数を見ると、10の位には必ず9があり、両側の2つの数を足すと、9になることが分かります。
つまりC『99(a−c)』というのは
『100d+90+(9−d)』という風にあらわせます。
この数を逆順にした数Dは
『100(9−d)+90+d』です。
この2つC、Dを足すと
『100d+90+9−d+900−100d+90+d』
→『900+90+90+9』
→『1089』になります。
【問題2】
1より大きな数をxとします。
xの逆数は(1/x)です。
1からこれを引くと、
『1−(1/x)』
→『(x/x)-(1/x)』
→『(x-1)/x』となります。
(x-1)/xの逆数はx/(x-1)です。
これを1から引くと、
『1-[x/(x-1)]』
→『[(x-1)/(x-1)]−[x/(x-1)]』
→『−1/(x-1)』となります。
この数の逆数は−(x−1)、つまり1−xです。
これにxを足せば、答えは1になります。
◆広島県 清川 育男 さんからの解答
【問題1】
A=X*100+Y*10+Z
0<X≦9,0<Z≦9,0≦Y≦9とおく。
1) X≧Z+2
A=X*100+Y*10+Z
B=Z*100+Y*10+X
A>B
C=A-B
=(X-Z)*100+Z-X
=(X-Z-1)*100+90+(10+Z-X)
D=(10+Z-X)*100+90+(X-Z-1)
C+D=900+180+9=1089
2) Z≧X+2
A=X*100+Y*10+Z
B=Z*100+Y*10+X
B>A
C=B-A
=(Z-X)*100+X-Z
=(Z-X-1)*100+90+(10+X-Z)
D=(10+X-Z)*100+90+(Z-X-1)
C+D=900+180+9=1089
1),2)から常に1089になる。
【問題2】
A>1とおく。
1/A
1/A-1=(1-A)/A
A/(1-A)
1-A/(1-A)=1+A/(1-A)=1/(1-A)
1-A
A+(1-A)=1
A>1であれば、常に1になる。
【おまけ】
百五減算パズルの応用問題ですね。
X=715A+364B+924C+1001N
Nは整数 (*)
X≡A (MOD 7)
X≡B (MOD 11)
X≡C (MOD 13)
1≦X≦1000 であるから
A=B=C=0はありえない。
例えば、A=5,B=5,C=5 のとき
X=715*5+364*5+924*5+1001N
=3575+1820+4620+1001N
=10015+1001N
≦1000
1≦X≦1000 N=-10
X=10015-10010=5
(*)は省略。
◆京都府 AAAI さんからの解答
【問題1】
答は1089です。
わかりやすくするため、
[a,b,c] は 100a+10b+c を表すとします
(例えば、[1,2,3]=123)。
ある3桁の数Aは、[x,y,z]で表せたとします。
ただし、x,y,zは0以上9以下の整数です。
当然、Bは[z,y,x]です。
題意より、z<x なので、くり下がりを考慮して
A-B を求めると [x-z-1,10+z-x] になります。
∵
[x-z,y-y,z-x]
=[x-z,0,z-x]
=[x-z-1,10,z-x]
=[x-z-1,10-1,10+z-x]
C は A-B で定義されていますので、
C=[x-z-1,9,10+z-x]、
D=[10+z-x,9,x-z-1] が成り立ちます。
よって
C+D
=[x-z-1,9,10+z-x]+[10+z-x,9,x-z-1]
=[(x-z-1)+(10+z-x),9+9,(10+z-x)+(x-z-1)]
=[9,18,9]
=9*100+18*10+9
=1089 となります。
【問題2】
答は1です。
最初に思い浮かべる数を A とします。
これの逆数は 1/A となり、これを1から引くと
(A-1)/A となります。
これの逆数は A/(A-1)、さらに1から引くと
(A-(A-1))/(A-1)=1/(A-1) となります。
最後にこれの逆数を取って(A-1)、最初に思い浮かべた数 A から引くと
A-(A-1)=1 となります。
【おまけ】
最初に思い浮かべる数を A、それを 7,11,13 で割った余りをそれぞれ x,y,z とします。
A=7a+x=11b+y=13c+z
(ただし、0≦x<7,0≦y<11,0≦z<13 かつ a,b,c は整数)
答は 715x+364y+924z を1001で割った余りです。
まず、次の式によって A を91(=7*13)で割った余りが求められます。
A=14A-13A
=(13*14c+14z)-(7*13a+13x)
=91(2c-a)+(14z-13x)
この余りを w とします。
w=14z-13x, d=2c-a, A=91d+w
次に、下の式によって A を1001(=91*11)で割った余りが求められます。
A=364A-363A
=4*91A-33*11A
=(11*364b+364y)-(91*363d+363w)
=1001(4b-33d)+(364y-363w)
この余り 364y-363w に w=14z-13x を代入します。
364y-363w
=7*13*4y-33*11*(14z-13x)
=11*13*33x+7*13*4y-7*11*66z
=11*13*(7*4+5)x+7*13*4y+7*11*(-13*6+12)z
=1001(4x-6z)+(11*13*5x+7*13*4y+7*11*12z)
以上より、余り、すなわち A は
11*13*5x+7*13*4y+7*11*12z
(=715x+364y+924z) となります。
【おまけ問題 略解】
A を求める式の形が、以下の通りであると仮定します。
A = px+qy+rz
ただし、A が1000を超える場合は、答は A を1001で割った余りとします。
また、x,y,z はそれぞれ最初に思い浮かべる数 A を 7,11,13 で割った余りとします。
係数 p,q,r について、x,y,z は互いに独立なので A を 7で割った余りが x となるにはp,q,r を 7で割った余りがそれぞれ、1,0,0 にならなければなりません。
同様に、A を 11で割った余りが y、 13で割った余りが z となるには、p,q,r を 11で割った余りがそれぞれ 0,1,0 、
13で割った余りがそれぞれ 0,0,1 にならなければなりません。
以上のことより
p は 7,11,13 で割った余りがそれぞれ 1,0,0
--> 143で割り切れ、 7で割ると 1余る整数
q は 7,11,13 で割った余りがそれぞれ 0,1,0
--> 91で割り切れ、11で割ると1余る整数
r は 7,11,13 で割った余りがそれぞれ 0,0,1
--> 77で割り切れ、13で割ると1余る整数
ということがわかります。
(p,q,r)=(715,364,924)
以上より、
715x+364y+924z を 1001 で割った余りが A になります。
●考察
この解法は、初めの仮定( A = px+qy+rz )の導き方をはっきりさせない限り、数学的な解法とはいえないでしょう
(そう思うのは私だけでしょうか)。
◆千葉県 緑川 正雄 さんからの解答
【問題1の回答】
必ず1089になる。
【理由】
思い浮かべた3桁の元の数Aを
A=a(1)×100+a(2)×10+a(3)とする。
但しa(1)、a(2)、a(3)は0〜9までの整数であり、
abs(a(1)-a(3))≧2
Aの百の位、十の位、一の位の数を逆順にした数(Bとする)は
B=a(3)×100+a(2)×10+a(1)
で与えられる。
(case1)A≧Bの時
機械的に計算すると
C=A-B
={a(1)×100+a(2)×10+a(3)}-{a(3)×100+a(2)×10+a(1)}
={a(1)-a(3)}×99
a(1)-a(3)=abs(a(1)-a(3))≧2であるから
a(1)-a(3)=2の時、C=198であり、D=891
a(1)-a(3)=3の時、C=297であり、D=792
a(1)-a(3)=4の時、C=396であり、D=693
a(1)-a(3)=5の時、C=495であり、D=594
a(1)-a(3)=6の時、C=594であり、D=495
a(1)-a(3)=7の時、C=693であり、D=396
a(1)-a(3)=8の時、C=792であり、D=297
a(1)-a(3)=9の時、C=891であり、D=198
全てC+D=1089となる。
(case2)A<Bの時
(case1)と同様である
【問題2の回答】
必ず1になる。
【理由】
最初にまず心の中に思い浮かべた1より大きな数をxとする。
その数の逆数をとり、それを1から引くと
1-1/x=(x-1)/x
もう一度、その答えの逆数をとり、それを1から引くと
1-1/{(x-1)/x}
=1-x/(x-1)
=-1/(x-1)
最後にその答えの逆数をとり、最初に考えた数を足すと
1/{-1/(x-1)}+x
=-(x-1)+X
=1
【おまけの回答】
元の数は7で割るとq余り、11で割るとs余り、13で割るとu余る時
1001を法として
-286×q+364×s-77×u
と合同な1から1000までの整数である。
【理由】
7,11,13は全て素数であり、互いに素(1以外の共通約数を持たない)
11×13=143,
13×7=91,
7×11=77も互いに素(1以外の共通約数を持たない)である。
具体的には
(-2)×143+4×91+(-1)×77=1
が成立する。
次に7×11×13=1001である。
1〜1000までの整数nがあって
(1)7で割るとq余る
即ちn=7×p+q (0≦q<7)
(2)11で割るとs余る
即ちn=11×r+s (0≦s<11)
(3)13で割るとu余る
即ちn=13×t+u (0≦u<13)
である時には、
n= {(-2)×143+4×91+(-1)×77}×n
= 7×11×13×{(-2)×p+4×r+(-1)×t}+{143×(-2)×q+91×4×s+77×(-1)×u}
= 1001×{-2×p+4×r-t}+{-286×q+364×s-77×u}
即ちnは、1から1000までの整数であってn≡-286×q+364×s-77×u [mod(1001)]
となる整数である。
◆石川県 魔術師ヤン さんからの解答
【問題1】
A=100a+10b+c と置く。
(a>b+1 a,b,cは、整数。)
aはbより2以上大きいとしたが、
100の位と1の位をひっくり返して、大きいほうから引くので、aとbの、大小関係を逆にしても同じになる。
B=100c+10b+a
A-B=99a-99c=99(a-c)=C
ここで、Cの、各位の数は、(a-c)によって決まる。
(a-c)は、2から9。
Cの各位の数を、a,cを使ってあらわすと、
100の位は、(a-c)-1
99*n (n=2,3,4,・・・・・9)を考えるとわかる。
10の位は、常に9
1の位は、10-(a-c) 百の位と似ている。
以上より、
C=100*(a-c-1)+90+10-(a-c)
=99a-99c
D=100*(10-a+c)+90+(a-c-1)
=99c-99a+1089
C+D=1089
以上から、一連の操作をすると常に結果は1089
【問題2】
ある数を、Xとすると、その逆数は、1/x
これを、1から引くと、
1-1/X=(X-1)/X
上の数の逆数は、X/(X-1)
これを、1から引くと、
1-X/(X-1)=-1/(x-1)
上の数の逆数は、-(X-1)/1=1-X
この数に、最初の数 X, を足すと
1-X+X=1
よって、答えは常に1となる。
【おまけ】
思い浮かべた数を、Xとすると、
X=7a+b (b=0,1,2,3,4,5,6)
X=11c+d (d=0,1,2,3,4,5,6,7,8,9,10)
X=13e+f (f=0,1,2,3,4,5,6,7,8,9,10,11,12) と、表せる。
(a,b,c)の組み合わせは、7*11*13=1001
a,b,cの、最小公倍数は、1001で、
(a,b,c)の組み合わせは、Xが、1001になると、1周期を迎える。
だから、a,b,cの値によって、Xが特定できる。
◆大阪府 Taketsuna さんからの解答
【問題1】
A=100x+10y+z とする。
x>z-1,x,y,zは0から9までの整数
B=100z+10y+x
A-B
=100(x-z)+z-x
=100(x-z-1)+90+(10+z-x)
=C
D=100(10+z-x)+90+(x-z-1)
C+D
=100(x-z-1 + 10+z-x)+90+90+(10+z-x + x-z-1)
=100×9+180+9
=1089
【問題2】
心に思い浮かべる数をxとする
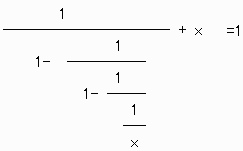
【おまけ】
いわゆる百五減算ですよね。
11と13の倍数で7で割って1余る数は715
7と13の倍数で11で割って1余る数は364
7と11の倍数で13で割って1余る数は924
頭の中で思い浮かべた数をNとすると
N= 7x+a
N=11y+b
N=13Z+c
715N= 5005x+715a
364N= 4004y+364B
924N=12012z+924c
辺々を加えて
2003N=1001(5x+4y+12z)+715a+364b+924c
N=1001(5x+4y+12z-2N)+ 715a+364b+924c
よって
7で割ったあまりを715倍
11で割ったあまりを364倍
13で割ったあまりを924倍し
それらを加えた数を1001で割ったあまりが求める数である。
◆石川県 平田 和弘 さんからの解答
【問題1】
まず、Aの百の位をa、十の位をb、一の位をc
(a>c+1)とすると、
A=100a+10b+c、
B=100c+10b+a なので
C=A−B
=(100a+10b+c)−(100c+10b+a)
=100(a−c)+(c−a)=99(a−c)・・・・・(★)
(要するに、a−c>1より、Cは99の倍数となることがわかります。)
ここで、
Cの百の位をa(1)(≠0)、十の位をb(1)、一の位をc(1)とすると、
C=100a(1)+10b(1)+c(1)、
D=100c(1)+10b(1)+a(1) なのですが、
C=99a(1)+{a(1)+10b(1)+c(1)}で、
a(1)≠0なので、(★)より
第二項{a(1)+10b(1)+c(1)}=99a(2)とおけるが、
a(1)、b(1)、c(1)は1〜9なので、a(2)=0、1 の場合しかありえません。
(∵a(2)>1では、{a(1)+10b(1)+c(1)}≧198とならなければならないが、
a(1)、b(1)、c(1)は1〜9なので、
{a(1)+10b(1)+c(1)}≦108となり矛盾する。)
1)a(2)=0 のとき、
a(1)=b(1)=c(1)=0 となってC=0 となり、Cが3桁の数になりません。
よって、このようなことはありえません。
2)a(2)=1 のとき、
{a(1)+10b(1)+c(1)}=99
このとき、b(1)>8 となります。
(∵b(1)≦8では、10b(1)≦80でかつ、a(1)、c(1)は1〜9なので、
{a(1)+10b(1)+c(1)}≦98で=99 とはなりえません。)
よってb(1)=9・・・・・(★2)
したがって、{a(1)+c(1)}=9・・・・・(★3)
C+D
={100a(1)+10b(1)+c(1)}+{100c(1)+10b(1)+a(1)}
=100{a(1)+c(1)}+20b(1)+{a(1)+c(1)}
=100×9+20×9+9
=900+180+9
=1089
で、答えは必ず1089となります。
【問題2】
単純に(かつ慎重に)計算して、
a+1/[1−[1/{1−(1/a)}]]
=a+1/[1−[1/{(a−1)/a}]]
=a+1/[1−[a/(a−1)]]
=a−1/[1/(a−1)]
=a−[a−1]
=1
となり、1です。
【おまけ】
求める数を7で割ったときの余りをa、
11で割ったときの余りをb、
13で割ったときの余りをcとします。
今、7×11×i が13で割ると1余るようにiを定め、
11×13×j が7で割ると1余るようにjを定め、
13×7×k が11で割ると1余るようにkを定めます。
i=12、j=5、k=4 がその1つの例となります。
このとき、求める数は
(7×11×i)×c+(11×13×j)×a+(13×7×k)×b =(7×11×12)×c+(11×13×5)×a+(13×7×4)×b =924c+715a+364bという形でかけます。
(∵7で割ると第一項、第三項は7で割り切れ、第二項の余りは1×a=aとなります。 11で割ると第一項、第二項は11で割り切れ、第三項の余りは1×b=bとなります。 13で割ると第二項、第三項は13で割り切れ、第一項の余りは1×c=cとなります。)これを7×11×13=1001で割った余り(0〜1000)が求める数となります。
ex.
a=1、b=1、c=1 のとき、
924+715+364=2003
2003÷1001=2...1 で求める答えは1
a=1、b=0、c=1 のとき、
924+715+0=1639
1639÷1001=1...638 で求める答えは638
a=1、b=1、c=0 のとき、
715+364=1079
1079÷1001=1...78 で求める答えは78
となります。
これは中国の剰余定理(孫子定理)の応用ですね。
◆ 問題へもどる
◆ 今週の問題へ