◆岩手県の中学校3年生 RYOTA さんからの解答
【問題1−1】
15×15×3.14×8=5652
(答)5652m3
【問題1−2】
1m3
=100cm×100cm×100cm
=1000000cm3
5652m3
=5652000000cm3
水1cm3は1gなので、
5652000000cm3
=5652000000g
=5652000kg
=5652t
【問題2】
らせん状の通路は、その円柱の展開図で考えた場合、
高さ50πmの一辺の一番上の頂点から、反対側の辺の一番上の頂点から、
50π/4m下の点へ結んだ斜めの直線となり、
そういう直線が50π/4m間隔で都合4本できる。
その1本の長さは、三平方の定理を用いて、
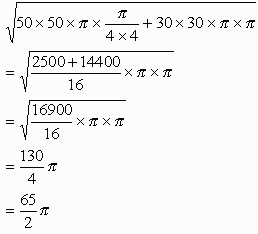
したがって、求める距離は、
65/2×π×4=130π
(答)130π m
◆石川県 平田 和弘 さんからの解答。
【問題1−1】
15×15×3.14×8=5652(m3) となります。
【問題1−2】
1リットル=0.1(m)×0.1(m)×0.1(m)=0.001(m3) のとき、1kgなので
1(m3)のとき、重さ1tとなります。
よって求める重さは5652(t)となります。
【問題2】
円柱側面の展開図を書くと、円周が
2×π×15=30π なので、
たて50π、よこ30πで上辺の中点をPとして下辺の中点をQとします。
また、たてを4等分した真中3つの中点を通るような図になるので、
直角三角形の、斜辺を除いた2辺が
15πおよび50÷8=6.25πなので、
三平方の定理または問題文中の三角比を使用して
斜辺が16.25πとなります。
求める経路の長さはこの斜辺を8回つなげた長さになるので、
16.25π×8=130π(m) となります。
【問題3】
問題2と同様に考えて図を書くと、経路は先ほどの斜辺と同様のものを7回つなげたものになります。
わかりやすくするためにPをA、QをHとします。
420÷7=60 なので、1つの斜辺の長さは60(m)となります。
Aから経路順に、60(m)ごとにB、C、D、E、F、Gと区切ります。
(要するにC、E、Gが左端にきて、同じ高さでまた右端にくるような図になります。)
(第1回目)
次郎がスタートで待っている間、太郎がBに達したとき真上・真下の位置になるので、
太郎はスタートから、
60/72=5/6(分)後、60(m)進んだ地点になります。・・・(★)
(第2回目)
まず、太郎がCまで達するのは
180/72=5/2(分)後なので、
この間次郎が3/2(分)進むので、H地点より、
36×3/2=54(m)進みます。
よってBC間は真上・真下の位置になりません。
次にCD間を考えて、太郎は先に1分間進むのでスタートより72(m)進みます。
要するに太郎はCより48(m)後方より進み、同時に次郎がスタートするとして、
(60+48)÷(72+36)=108/108=1(分)後、真上・真下の位置になります。
要するに、太郎はCより
72−48=24(m)進んだ地点(Dまで残り36(m))、次郎はHより36(m)進んだ地点となります。
言いかえれば、太郎はスタートから2(分)後、144(m)進んだ地点になります。
また次郎は、スタートから
1(分)後、36(m)進んだ地点になります。・・・(★)
(第3回目)
次郎は2回目の地点よりGまで達するのは
24/36=2/3(分)後なので、
この間太郎は2回目の地点より
72×2/3=48(m)進みます。
よってDより24+48−60=12(m)進みます。
太郎と次郎はこの地点より、
(60−12)÷(72+36)=48/108=4/9(分)後、真上・真下の位置になります。
要するに、太郎はDより
12+{72×(4/9)}=44(m)進んだ地点(Eまで残り16(m))、
次郎はHより36×(4/9)=16(m)進んだ地点となります。
言いかえれば、太郎はスタートから
2+80/72=28/9(分)後、224(m)進んだ地点になります。
また次郎は、スタートから
1+16/36=13/9(分)後、76(m)進んだ地点になります。・・・(★)
(第4回目)
太郎は3回目の地点よりEまで達するのは
(60−44)/72=2/9(分)後なので、この間次郎は3回目の地点より
36×(2/9)=8(m)進む。
よってGより16+8=24(m)進む。
さらに太郎はこの地点によりGまで達するのは
120/72=5/3(分)後なので、この間次郎はさらに、
36×(5/3)=60(m)進む。
よってFより24(m)進む。
太郎と次郎はこの地点より、
(60−24)÷(72+36)=36/108=1/3(分)後、真上・真下の位置になります。
要するに、太郎はGより
72×(1/3)=24(m)進んだ地点(Hまで残り36(m))、
次郎はFより
24+{36×(1/3)}=36(m)進んだ地点となります。
言いかえれば、太郎はスタートから
2+240/72=16/3(分)後、384(m)進んだ地点になります。
また次郎は、スタートから
1+96/36=11/3(分)後、156(m)進んだ地点になります。・・・(★)
また、4回目の地点よりHまで達するのは
(60−24)/72=1/2(分)後なので、この間次郎は4回目の地点より
36×(1/2)=18(m)進む。
よってFより24+18=42(m)進むが、真上・真下の位置になりません。
【問題3別解】
真上から見た平面図(円周)で考えてみます。
420(m)で3周半するので、1周あたり、
420÷3.5=120(m)(半周では60(m))となります。
今、上から見ると円の直径をはさんで反対側より、太郎が反時計まわり、次郎が時計まわりに進むと考えます。
この図で、太郎と次郎が重なる位置が螺旋の真上・真下の位置になるのでこの位置を太郎がQに到着するまで、要するに
420/72=35/6分までの範囲で求めればよいことになります。
まず、第1回目に重なるのは、次郎が待っている間に太郎が半周した(60(m)進んだ)とき
重なるので、スタートより
60/72=5/6(分)後となります。
次に太郎が1分間進んだとき、太郎は重なりの地点より
72−60=12(m)左回りに進んでいるので、両者の円周上の距離は
120−12=108(m)となります。
両者は1分間に72+36=108(m)ずつ近づくので、
108÷108=1(分)後に重なります。
要するに太郎がスタートしてから1+1=2(分)後に重なります。
この後は両者の円周上の距離は120(m)と考えて、両者は1分間に
72+36=108(m)ずつ近づくので、
120÷108=10/9(分)後ずつに重なります。
よって太郎がスタートしてから
2+10/9=28/9、
2+2×(10/9)=38/9、
2+3×(10/9)=16/3=(32/6)(分)後に重なります。
ここでこのうち、両者が真上・真下ではなく出会うところ(同じ地点)が1か所あるのでこれを求めて除けばよいことになります。
次郎がスタートしたとき(太郎がスタートして1(分)後)の両者の実際(経路上)の距離差は
420−72=348(m)で、両者は1分間に
72+36=108(m)ずつ近づくので、
348÷108=29/9(分)後に出会います。
即ち太郎がスタートしてから
1+29/9=38/9(分)後に出会います。
以上より求める答えは、太郎がスタートより
5/6、2、28/9、16/3(分)後の地点となります。
◆石川県 Takashi さんからの解答
【問題1−1】
V=3.14×152×8
=5652【m3】
【問題1−2】
【問題2】
点Qから点Pまで昇る時、円柱の周囲をまわる回数をnとする。
【nは自然数】
直線PQ上に注目すると、通路を一周するたびに
50π/nづつ上の点を通過している事がわかる。
この円柱をn等分して、半径15m、高さ50π/nの円柱をつくり、側面を直線PQで切断して展開図にすると、
側面全体は、横の長さ30π、縦の長さ50π/nの長方形になり螺旋通路の軌跡は左下から右上の対角線になる。
対角線の長さは、
L={(30π)2+(50π/n)2}0.5
=(10π/n)×(9n2+25)0.5
この小さな円柱がn個集まると元の円柱が出来るのだから、通路の総距離は、
nL=10π×(9n2+25)0.5
螺旋通路の周回数は4回【n=4】という条件で、側面の展開図を4枚横に並べると、
50π×120πの長方形が出来あがって、対角線の長さは130πという題意だったのでしょうか。
【コメント】
出題の最初の段階で、5階という条件を書き忘れ、ご迷惑をおかけしました。
【問題3】
螺旋通路は3周半で総距離は420mであるから、1周の距離は
420÷3.5=120
スタートから1分後、太郎は72メートル進んでいるから、次郎の上を過ぎてから12m進んだところにいる。
そこで次郎がスタートしてから、2人が最初に上下に並ぶまでの時間をt【分】とすると、
120=72×t+36×t+12
t=1【分】
次に、2人が上下に並ぶまでの時間をu【分】とすると、
120=72×u+36×u
u=10/9【分】
次郎がスタートしてから2人が出会うまでの時間をs【分】とすると、
420=72×(s+1)+36×s
s=29/9【分】
太郎と次郎がちょうど上下の関係になるのは、
次郎がスタートする10秒前
次郎がスタートして1分後
次郎がスタートして19/9分後、の3回
太郎と次郎がちょうど出会うのは、
次郎がスタートして29/9分後、の1回
次郎が上になるのは、
次郎がスタートして39/9分後
次郎がスタートして20/3分後
【太郎がQ地点で立って待っているとしたとき】
次郎がスタートして10分後【上に同じ】、の3回
以上、7回。
◆広島県 清川 育男 さんからの解答
【問題1−1】
15×15×3.14×8=5652(m3)
答え 5652m3。
【問題1−2】
水1m3の重さ1t(トン)
答え 5652t。
【問題2】
円周の長さ 30π(m)
4周の長さ 120π(m)
勾配は120πmいって50πm上がる。
三角形の三辺の比が、5:12:13のとき直角三角形。
この場合、通路の長さは、130πmとなる。
答え 130πm。
【問題3】
真上、真下の関係は120mの倍数の差で表現出来る。
1)
太郎が出発してχ分後にあるとする。
420−72χ=360
χ=5/6<1
2)
次郎が出発してχ分後にあるとする。
420−(72+72χ+36χ)=240
χ=1
3)
次郎が出発してχ分後にあるとする。
420−(72+72χ+36χ)=120
χ=19/9
4)
次郎が出発してχ分後にあるとする。
420−(72+72χ+36χ)=−120
χ=13/3
太郎が歩いた距離は、
72+72×13/3=384<420
以上、4回が題意を満たす。
答え 4回。
◆千葉県 緑川 正雄 さんからの解答
【問題1−1の回答】
水そうの体積
=3.14×15×15×8
=5652(m3)
【問題1−2の回答】
水の重さは1m3あたり1トンであるから
5652トン
【問題2及び問題3】
・地点Qから地点Pに着くまでの回転数をnとする。
・地点Pの真下からの高さをH(m)とする。
・円柱の円の部分の半径をr(m)とする。
この場合、円柱の周りの‘回転距離’は
(2πr)×n=2nπr(m)
鉛直方向の上昇距離はH(m)である。
よって、起点Qから終点Pまでの距離Lは、
![]()
【問題2の回答】
r=15(m),H=50π(m)を代入すると
L2=(30×nπ)2+(50π)2
n=4を代入すると
L2=(120π)2+(50π)2
=(130π)2
より、L=130πを得る。
答え408.2m
【問題3の回答】
L=420(m),H=21(m),n=3.5(回転)である。
一方1回転すると420/3.5=120(m)の距離を進む。
太郎が出発した時刻をt=0(分)とする。
時刻t(分)における、太郎及び次郎がいる地点のQを基準に取った距離x,yは、
t≧1において
x=420-72×t,y=36×(t-1)
が成立し、0≦x,y≦420(m)が成立しなくてはならないので
1≦t≦35/6の範囲で回答を求める。
2人の距離の差Sは
S=x-y=456-108×t で表され、太郎と次郎が互いに真上と真下にいる場合には、
S=120×k (Kは整数)が成立しなくてはならない。
すなわち、456-108×t=120×kより
-1.45≦k≦2.9の関係式を得る。
よってk=-1,0,1,2であり、
(t,k)=(16/3,-1),(38/9,0),(28/9,1),(2,2)
太郎が出発してから
2分後,28/9分後,38/9分後,16/3分後に太郎と次郎は互いに真上と真下にいる。
【コメント】
38/9分後は2人が同じ場所で出会う時間です。
◆ 問題へもどる
◆ 今週の問題へ