です。ＡＢを「正方形の穴の対角線」に重ね、ＣＥを「穴の開いている平面」に常に平行にするようにして、穴を通します。
ＡＢが穴を通る瞬間が問題ですが、平面に垂直にわずかにずらせば、Ａ，Ｂを穴に触れることなく通すことが可能です。
【おまけ１】は可能が正解です。
正八面体の頂点間で最長なのは例えばＡＢで、その長さはです。
ＡＢを「正方形の穴の対角線」に重ね、ＣＥを「穴の開いている平面」に常に平行にするようにして、穴を通します。
ＡＢが穴を通る瞬間が問題ですが、平面に垂直にわずかにずらせば、Ａ，Ｂを穴に触れることなく通すことが可能です。
通過可能な正方形の穴の一辺の最小値を求めるのは難しいでしょうね。
【おまけ２】には、回答がきませんでした。
どうも問題が誤りで、出題されたのは正二十面体のようです。
（訂正しました）
正二十面体の場合は、
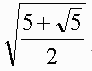
になるようです。
◆Miki Sugimotoさんからの証明。
[ Proof ]
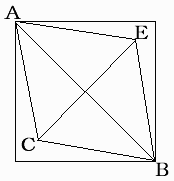
一辺の長さが１の正五角形ＡＢＣＤＥを考えたとき、
ＡＣ＝(１＋
)/２
である。 (証明略、相似などを使う。)
さて、正20面体のある任意の一辺をＰＱとする。
それと丁度反対側の辺をＲＳとする。
題意はＰＲの長さを求めることにある。
四角形ＰＱＲＳは (対称性より) 長方形であり、
ＱＲ＝ＳＡ＝(１＋)/２
であったから、
ＰＲ2＝１2＋{(１＋)/２}2
∴ ＰＲ2＝(５＋)/２
i.e ＰＲ＝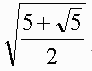
正十二面体が解けた方は教えてください。
◆広島県 清川 育男 さんからの解答。
【問題１】
３６０−（１２０×２＋６０）＝６０
７２０÷６０＝１２
１２×３÷２＝１８
１８−１２＋２＝８
答え 頂点 １２個 辺 １８個 面 ８個。
切頂四面体であるから
もとの正四面体の面は４個、頂点は４個から面の数は８。
【問題２】
３６０−（１４４×２＋６０）＝１２
７２０÷１２＝６０
６０×３÷２＝９０
９０−６０＋２＝３２
答え 頂点 ６０個 辺 ９０個 面 ３２個。
切頂十二面体であるから、
もとの正十二面体の面は１２、頂点は２０から面の数は３２。
正三角形の個数をＸ、正十角形の個数をＹとする。
Ｘ＋Ｙ＝３２
３Ｘ＋１０Ｙ＝９０×２
７Ｙ＝８４
Ｙ＝１２（正五角形が正十角形になったと考える。）
Ｘ＝２０（正十二面体の頂点の数２０と同じになる。）
答え 正三角形 ２０個 正十角形 １２個。
【問題３】
３６０−（６０＋９０×２＋１０８）＝１２
７２０÷１２＝６０
６０×４÷２＝１２０
１２０−６０＋２＝６２
答え 頂点 ６０個 辺 １２０個 面 ６２個。
正三角形の個数をＸ、正方形の個数をＹ、正五角形の個数をＺとする。
Ｘ＋Ｙ＋Ｚ＝６２
３Ｘ＋４Ｙ＋５Ｚ＝６０×４
３Ｘ＝４Ｙ÷２
Ｘ＝２０、Ｙ＝３０、Ｚ＝１２
答え 正三角形 ２０個 正方形 ３０個 正五角形 １２個。
【おまけ１】
正八面体は正方形を底面に上下に正三角形が８個ある正多面体と考えることが出来るので、方向を合わせることで正方形の穴を通過させることが出来る。
◆東京都 Asami (^_^) さんからの解答。
【問題１】
４頂点を切り落としたので面の数が４つ増えるので
面の数＝８
頂点数は３倍になるので
頂点数＝12
オイラーの定理から
辺の数＝18
【問題２】
正十二面体(各面が正五角形)の各頂点を切り落としたものと考えることができるので、
面の数＝正十二面体の頂点数＋12＝20＋12＝32
頂点数＝12×3＝36
オイラーの定理より辺の数＝66
【問題３】
正十二面体の各五角形を浮かしたものと考えると、
正方形の数＝五角形の辺の総数÷2＝30
正三角形の数は正二十面体の各三角形を浮かしたものと考えると、
正三角形の数＝20
従って
準正多面体の面の数＝12＋30＋20＝62
辺の数＝(20×3＋30×4＋12×5)÷2＝120
オイラーの定理より
頂点数＝60
【おまけ１】
可能。
正八面体は２つのピラミッド形を底面同士でくっつけたものと考えることができ、その面と正方形の穴が一致させるような形で通過させるとよい。
【おまけ２】
正十二面体に内接する立方体の対角線の長さが、正十二面体の最も長い対角線に相当すると嬉しいな。
じゃなかったら求めるのはけっこう大変なのでは？
(といって逃げる…(笑))
◆長崎県 Dr.Berserker さんからの解答。
【問題１】
正四面体の頂点の数は４つなので、この分だけ、面が増えることになります。
したがって、面の数は、４＋４＝８。
次に、頂点の数ですが。切り口は三角形になるので、頂点の数は３倍になることが分かります。
したがって、頂点の数は、４×３=１２。
【問題２】
この立体は、もとは正１２面体であったはずなので、正１２面体の頂点の数は、
１２×５÷３=２０。
したがって、１２＋２０＝３２面体ということが分かります。
また、頂点の数は、２０×３=６０となります。
三角形の数は、元の正１２面体の頂点の数と同じなので、２０。
正１０角形は、元の５角形の面がそのまま残っているので、１２個ということになります。
【問題３】
この立体では、何を切ったとかいうのは、はっきり言って無駄ですね。
純粋にやってみます。
まず、頂点の数から。
この立体の一つの頂点には、三角形、四角形×２、五角形がそれぞれ一つづつ集まっています。
したがって、この角の尖度は、
３６０−（６０＋９０×２＋１０８）＝１２
なので、頂点の数は、
７２０÷１２＝６０
ということになります。
よって、組み合わせの理論より、一つの頂点から、４つの頂点へ、辺が引けるので、辺の数は、
６０×４÷２＝１２０
ということになります。（少し多いような・・・）
最後に面の数ですが、これは別々にやっていくしかないように思えます。
まず、五角形ですが、互角形にくっついていない頂点はないので、
６０÷５＝１２
が、五角形の数になります。
次に四角形ですが、これは、一つに頂点に、二つの四角形がくっついているので、
６０×２÷４＝３０
が、四角形の数になります。
最後に三角形の数ですが、これも五角形と同じように、
６０÷３＝２０
が、三角形の数になります。
以上より、面の数は、
１２＋３０＋２０＝６２
が、答えになります。（これで、辺の数も合う。）
◆石川県 平田和弘 さんからの解答。
(問題１解答)
１つの頂点に正三角形１つと正六角形２つが集まっているので、１つの頂点の尖度は
360−(60＋120×2)＝60°
よって頂点の数は、720°÷60°＝12 個
また１つの頂点に３辺が集まっているので、
求める辺の数は、(3×12)÷2＝18 本
従って面の数は、オイラーの多面体定理より、18−12＋2＝8 面となります。
(問題２解答)
１つの頂点に正三角形１つと正十角形２つが集まっているので、１つの頂点の尖度は
360−(60＋144×2)＝12°
よって頂点の数は、720°÷12°＝60 個
また１つの頂点に３辺が集まっているので、
求める辺の数は、(3×60)÷2＝90 本
従って面の数は、オイラーの多面体定理より、
90−60＋2＝32 面となります。
このとき、正三角形の数および正十角形の数は、
1.
もとの多面体が正十二面体で、その頂点を正三角形に削り取った形なので、
正十二面体の頂点の数は20個、面の数は12面なので
正三角形の数は20個、正十角形の数は12個 となります。
2.
また、もとの多面体がわからなくても、正三角形の数をx、正十角形の数をyとおくと
面の関係より、ｘ＋ｙ＝32
辺の関係より、(3x＋10y)÷2＝90
となりこれらの連立方程式を解くとx＝20、y＝12 となるので
正三角形の数は20個、正十角形の数は12個 となります。
(問題３解答)
１つの頂点に正三角形１つと正方形２つと正五角形１つが集まっているので、１つの頂点の尖度は
360−(60＋90×2＋108)＝12°
よって頂点の数は、720°÷12°＝60 個
また１つの頂点に４辺が集まっているので、
求める辺の数は、(４×60)÷2＝120 本
従って面の数は、オイラーの多面体定理より、
120−60＋2＝62 面となります。
このとき、正三角形の数、正方形の数および正五角形の数は、正三角形の数をx、正方形の数をy、正五角形の数をzとおくと
面の関係より、ｘ＋ｙ＋z＝62・・・(1)
辺の関係より、(3x＋4y＋5z)÷2＝120
よって、xを消去して、y＋2Z＝54 ・・・(2) が得られる。
そして、正五角形とそのまわりの正方形についてみると、正五角形辺は正方形の２辺ずつと辺を共有しているので
(要するに正五角形の辺の合計は正方形の辺の合計の半分に等しいので)
5Z＝(4y/2) 即ち、5z＝2y・・・(3) が得られる。
したがって(2),(3)よりZ＝12、y＝30 となり、この結果を(1)に代入してx＝20 となる。
求める正三角形の数は20個、正方形の数は30個、正五角形の数は12個 となります。
(感想)
問題３の連立方程式の第３の関係をみつけるのに苦労しました。
オイラーの多面体定理はいまさらながら素晴らしいと思います。
(定理自体が簡単なだけに余計そう感じます。)
(おまけ１解答)
イ.
四角形AFBDをそのまま通そうとする(EおよびCを寝かせる格好で)と、四角形AFBDを穴のあいた平面に対してどのように傾けても、
AF＝BD＝AD＝BF＝1のため通過させることができない。
ロ.
また、EとCを穴の対角線に通そうとしても、問題の中にあるJavaAppletのスタートをEを真上から見た図として考える。
1.より、AFは1辺が1の正三角形の底辺であることがわかり、
EからADにおろした垂線がADと交わる点をPとすると、
EPの長さは三平方の定理で、EP＝
/2 ・・・(1)です。
Eから四角形AFDBにおろした垂線が交わる点をQとすると、QはEを四角形AFBDに投射した点になるので3.の事実より、
∠QAF＝∠QAD＝∠QFA＝∠QFB
＝∠QDA＝∠QDB＝∠QFB＝∠QBF となるので
∠FAD＝∠AFB＝∠ADB＝∠DBF＝90°となります。
また2.より四角形AFBDはひし形でありますので、平行四辺形(AD//FB、AF//DB)でもあります。
よって、四角形AFBDは正方形となり、PQ＝1/2 ・・・(2)となります。
△EPQに三平方の定理を適用して、
EQ2＋PQ2＝EP2で、これに(1),(2)を代入して
EQ2＋1/4＝3/4
即ち、EQ＝/2 となります。
よってEC＝2・EQ＝ なので、1辺が1の長さの対角線はで同じであるのでECを平面に対して少し傾ければ(要するECが平面に平行にならないようにすれば)通せる。
以上ロ.より通すことは可能。
◆ 問題へもどる
◆ 今週の問題へ
数学の部屋へもどる。