◆北海道 k.yoshida さんからの解答。
【問題1】
0.5倍
【問題2】
6番目
【問題3】
問題2が大きなヒントになりました。
すなわち,ある三角形の下側の辺の長さがそのすぐ前の辺の何倍になるのかと考えました。
そこで,下側の辺 (1)(2)(3)・・・(N-1)(N) の長さを
(L1)(L2)(L3)・・・(Ln-1)(Ln)としたとき,
L2=1/2*L1,
L3=3/4*L2=3/4*1/2*L1,
L4=5/6*L3=5/6*3/4*1/2*L1,
L5=7/8*L4=7/8*5/6*3/4*1/2*L1
・
・
・
同様にして
Ln=1/2*3/4*5/6*7/8*9/10*・・・・・・(2n-1)/2n*L1
従って求める解は
Ln/L1=1/2*3/4*5/6*・・・・・(2n-1)/2n
これをすっきりした形にし,さらに証明しなければいけないと思いますが,大学受験からすでに20年強経ってますのでよく分かりませんでした。
◆広島県 清川 育男 さんからの解答。
【問題1】
くさび形の木片の底辺に長さx、斜辺に長さyの最初の三角形を決める。
底辺に対する高さをcとする。
次の三角形の面積が最初のそれに等しくなるためには、斜辺に対する高さ(d)が等しいので、さらに斜辺にyの長さをとればよい。
相似の関係から底辺(2)の三角形の高さは、
y:2y=c:2c 2cとなる。
したがって底辺(2)の長さは1/2*xとなればよい。
答え 1/2。
【問題2】
(4)の辺の長さ 5/16。
(5)の辺の長さ
5/16*7/8=35/128>1/4
(6)の辺の長さ
35/128*9/10=63/256<1/4
答え (6)
【問題3】
問題1,問題2から底辺と斜辺の長さの決め方に下記の関係がみられる。
1*(1/2)=1/2,
1*(2/3)=2/3,
1/2*(3/4)=3/8,
2/3*(4/5)=8/15,
3/8*(5/6)=5/16,
8/15*(6/7)=16/35,
5/16*(7/8)=35/128
奇数番が底辺、偶数番が斜辺の長さ。
奇数番だけをとりあげると、
c(n)=c(n−1)*(2n−3)/(2n−2)
n≧2。
上記の漸化式が成り立つ。
◆東京都 Asami さんからの解答。
【問題1】
1/2倍
【問題2】
n=5のとき35/128
n=6のとき63/256
従って、はじめて1/4以下となるのはn=6
【問題3】
(1):1
(2):1×1/2
(3):(1+1/2)×1/4=3/8
(4):(1+1/2+3/8)×1/6=35/16
………
………
(n):
たとえば(4)の(1+1/2+3/8)部分をS3などと置く。
すると、
Sn
=1・3/2・5/4・7/6・…・{2(n-1)+1}/2(n-1)
(n≧2)…★
={2(n-1)+1}!/4n-1・{(n-1)!}2
となる。
また
(n)=Sn-1・1/2(n-1)だから、
={2(n-2)+1}!/2・4n-2・{(n-2)!}2・(n-1)
(n≧3)
となる。(実はn≧2でよい)
随分とヘンテコな式になりましたが………
見やすくするためには★の形をとればいいかと思います。
◆富山県 いくまる さんからの解答。
(2N-1)個目の三角形を切り取ったとき、その三角形の底辺がN番目の辺となる。
これをA_Nとする。
Nが2以上のとき、
(2N-1)番目の三角形と、1番目から(2N-2)番目までを併せた三角形を考えると、
面積比は1:(2N-2)、
共通な高さを持つとすると、底辺の比はA_N:{A1+A2+‥A_(N-1)}、
よって
1:(2N-2) = A_N:{A1+A2+‥A_(N-1)}
2(N-1)・A_N = A1+A2+‥A_(N-1) ‥(1)
Nを1つ増やした式を考えると、
2N・A_(N+1) = A1+A2+‥A_(N-1)+A_N ‥(2)
(2)-(1)から
2N・A_(N+1) - 2(N-1)・A_N = A_N
2N・A_(N+1) = (2N-1)・A_N
A_(N+1) = {(2N-1)/2N}・A_N
となる。
(2N-1)/2N<1であるから、数列{A_N}は単純減少である。
一般項A_Nは
A_N = [ {1×3×‥×(2N-3)}/{2×4×‥×(2N-2)} ]A1
となる。
A2 = (1 / 2 ) A1 =(1/2)A1
A3 ={(1×3 )/(2×4 )}A1=(3/8)A1
A4 ={(1×3×5 )/(2×4×6 )}A1=(5/16)A1
A5 ={(1×3×5×7 )/(2×4×6×8 )}A1=(35/128)A1
A6 ={(1×3×5×7×9)/(2×4×6×8×10)}A1=(63/256)A1 ((<1/4)A1)
問題1:1/2
ヒントに気づかないとこれは難問ではないでしょうか。
もう一本の半直線にできる辺の長さをB_Nとすると、
A_N =1/(B1+B2+‥+B_N)
B_N =1/{A1+A2+‥+A_(N-1)}
という比較的きれいな漸化式が立ったのですが、どうしても連分数が処理できず、give upしてヒントを見てしまいました。
この連立漸化式を解くにはどうすれば良いのでしょうか、、、、
◆海外 西野 友朗 さんからの解答。
「高さが同じ三角形の面積の比と底辺の長さの比は等しい」という性質を利用して考えます。
便宜上、問題上の(1)、(2)、...、(N)の長さをそれぞれ
L(1)、L(2)、...、 L(N)と表記し、L(1)=1とします。
1.
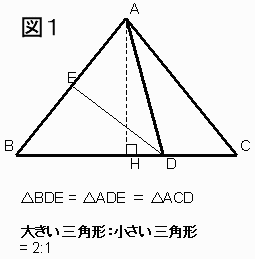
L(1)とL(2)の関係を見るために、木片の各頂点に以下のように名前をつけます
(図1参照)。

△ABDと△ACDは高さが共にAHなので、面積の比と底辺の比は等しくなります。
△ABDを構成する△ADEと△BDE、そして△ACDの面積は題意からいずれも等しいので、△ABDと△ACDの面積比は2:1になります。
よって、
L(1):L(2) = 2:1、
L(2) = L(1)/2 = 1/2
2.
次にL(1) 、L(2)とL(3)の関係を見ます。
先程と同様に考えると(図2参照)、
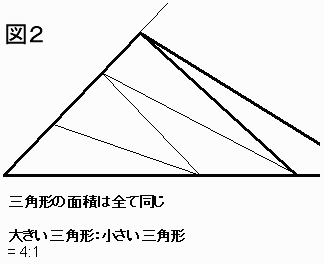
{L(1)+L(2)}:L(3) = 4:1 となることがわかります。
L(1)+L(2) = (1x2)/2+1/2 = 3/2より、
L(3) = {L(1)+L(2)}/4 = 3/8
3.
さらに L(4)との関係を見ます。同様に(図は省略)、
{L(1)+L(2)+L(3)}:L(4) = 6:1となります。
L(1)+L(2)+L(3) = (3x4)/8+3/8 = 15/8より、
L(4) = {L(1)+L(2)+L(3)}/6 = 15/48
4.
以下、一般項を考えます。
L(N)を計算する過程を分子LU(N)・分母 LL(N)に分けて考えると、
LU(1) = 1、
Nが2以上のとき、
LU(N) = LU(N-1)x {2(N-2)}+LU(N-1) = LU(N-1)x(2N-3)
これは、初項が 1、公比が1、3、5、 ...(以下奇数が続く)と徐々に大きくなる数列を示します。
LL(1) = 1
Nが2以上のとき、LL(N) = LL(N-1)x2(N-1)
これは、初項が1、公比が2、4、6、 ...(以下偶数が続く)と徐々に大きくなる数列を示します。
LU、LLを組み合わせて、
L(1) = 1
Nが2以上のとき、
L(N)
= LU(N)/LL(N)
= {1x1x3x5x7x..(奇数)..x(2N-3)}/{1x2x4x6x8x..(偶数 )..x2(N-1)}
【問題1】
L(2) = 1/2
【問題2】
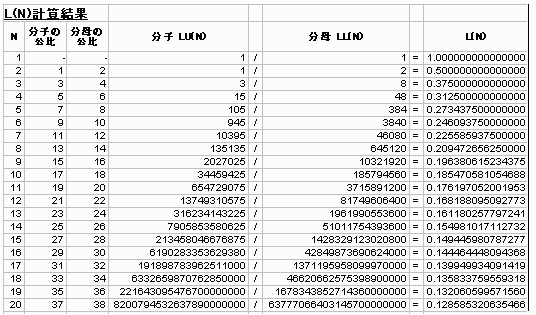
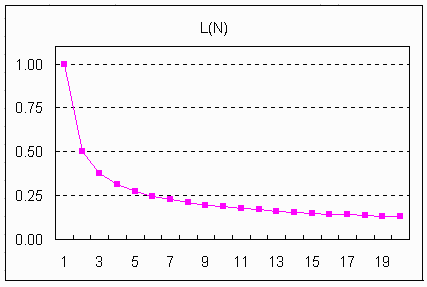
L(N)を計算した結果によると(「計算結果」シート参照)
L(5) = 0.27343750、
L(6) = 0.24609375となるので、(6)番目
【問題3】
上記の通り
問題 3がこれで解けたと言っていいのかどうか…。
「数列の積の公式」みたいなものがあって、もっと簡単になるような気がするのですが、WEBで見つけることができなかったので、ここで打ち止めにしました。
これはこれで見た目がきれいなのですが、実際に計算するのは大変ですね。
◆石川県 平田 和弘 さんからの解答。
(問題1解答)
くさび形の頂点をO、Oから下側の辺に長さLの点をとりA1、A1からさらに長さLの点をとりA2とし、Oから上側の辺に長さMの点をとりB1、B1からさらに長さMの点をとりB2とします。
題意より
△OA1B1の面積=△A1B1B2の面積なので
(高さはともに共通だから)、・・(a)
線分OB1=線分B1B2となります。
線分OA1:線分OA2=線分OB1:線分OB2なので
線分A1B1と線分A2B2は平行 であり
△OA1B1の面積:△OA2B2の面積=1:22=1:4・・・(b)
従って△OA1B1の面積=Sとすると
△A1A2B2の面積
=△OA2B2の面積−△OA1B1の面積−△A1B1B2の面積
=4S−S−S
=2S
となり元の三角形の2倍の大きさになります。
元の三角形と同じ面積にするには線分A1A2の中点に点A3をとればよい。
従って求める(2)の辺の長さは最初(1)の下側の辺の長さの1/2となります。
(問題2解答)
問題1の(a)および(b)の原理を使って(かなり計算が面倒ですが)各々三角形の下側の辺の長さを計算すると以下のようになります。
| 三角形 | 下側の三角形の 下側の辺の長さ |
| (1) | L |
| (2) | 1/ 2L |
| (3) | 3/ 8L |
| (4) | 5/ 16L |
| (5) | 35/128L |
| (6) | 63/256L |
| ・ ・ ・ |
となり63/256<64/256=1/4なので、
(6)のとき初めて元の辺の長さの1/4以下になります。
(問題3解答)
一般項はよくわかりませんが次の関係が見出せます。
問題2と同様に問題1の(a)および(b)の原理を使って(かなり計算が面倒ですが)今度は上側の各々三角形の上側の辺の長さを計算すると以下のようになります。
(上側の最初の辺の長さをMとする。)
| 三角形 | 上側の三角形の 上側の辺の長さ |
| (1) | M |
| (2) | M |
| (3) | 2/ 3M |
| (4) | 8/ 15M |
| (5) | 16/ 35M |
| (6) | 128/315M |
| ・ ・ ・ |
となりますので改めて整理すると
| 側 | (1) | (2) | (3) | (4) | (5) | (6) |
| 上 | 1 | 1 | 2/3 | 8/15 | 16/35 | 128/315 |
| 下 | 1 | 1/2 | 3/8 | 5/16 | 35/128 | 63/256 |
関係をしらべるために分母・分子を変更すると
| 側 | (1) | (2) | (3) | (4) | (5) | (6) |
| 上 | 1/1 | 1/1 | 2/3 | 8/15 | 48/105 | 384/945 |
| 下 | 1/1 | 1/2 | 3/8 | 15/48 | 105/384 | 945/3840 |
となり下側の辺は分母が1→2→8→48→384→3840となり、それぞれ
1→ 2 は ×2
2→ 8 は ×4
8→ 48 は ×6
48→ 384 は ×8
384→3840 は ×10
で求められます。
第n項まで偶数を次々掛けていく。
(2×4×6×8×10×・・・)
また分子は上側の第n項の分母をそのまま分子にすればよいのですが、
上側の辺は分母が1→1→3→15→105→945となり、それぞれ
1→ 1 は ×1
1→ 3 は ×3
3→ 15 は ×5
15→ 105 は ×7
105→ 945 は ×9
で求められます。
第n項まで奇数を次々掛けていく。
(1×3×5×7×9・・・)
たとえば第8項めは、
分母が2×4×6×8×10×12×14=645120
分子が1×3×5×7×9×11×13=135135 なので
下の辺の長さは元の辺の長さの
135135/645120となります。
(感想)
問題1はあることに気がつくと比較的やさしい。
問題2は計算がなかなか大変ですので、根気良くやればできます。
問題3は最初さっぱりわかりませんでしたが、無理矢理考えた結果こうなりましたので 自信はありません。
もっと簡単にできるような気がしますが.......。
最初座標軸がありましたので何か関係があるのかと思いましたが本当は何も関係ないことに(やっているうちに)気がつきました。
計算がかなり大変なので(もしかしたらもっとうまくできるのかもしれませんが)、おもしろい問題とは思いますがあまり良問とはいえないと思います。
最初のうちは図をたくさん書きましたがしまいに図も書けなくなって計算のみになりましたが、ここらあたりまでくると電卓を持ち出さないとできない始末でした。
◆静岡県 ヨッシー さんからの解答。
【問題1】
1/2倍
【問題2】
(6)
【問題3】
(N)の長さを a(N) ,a(1)=1とすると
a(1):a(2)=2:1
a(1)+a(2):a(3)=4:1
a(1)+a(2)+a(3):a(4)=6:1
| a(N)= | N-1 Σ k=1 | a(k) ――――― 2(N-1) |
| a(N+1)=( | N-1 Σ k=1 | a(k)+a(N))/2N |
| 2N・a(N+1)= | N-1 Σ k=1 | a(k)+a(N) |
| (2N-2)・a(N)= | N-1 Σ k=1 | a(k) |
引き算して
2N・a(N+1)−(2N-2)・a(N)=a(N)
a(N+1)=a(N)×(2N-1)/2N
よって、
a(N)=a(1)×{1・3・5・・・(2N-3)}/{2・4・6・・・(2N-2)}
答え:{1・3・5・・・(2N-3)}/{2・4・6・・・(2N-2)}倍
◆神奈川県 焼き餃子 さんからの解答。
【問題1】
(2)の辺の長さは(1)の辺の長さの何倍でしょうか。
左端の頂点から、m番目の三角形の右辺を含めた全体の三角形の面積をS(m)とし、分割された個々の三角形の面積をsとおく。
m番目までの三角形の底辺と斜辺の長さをa(m),b(m)とおく。
すると、
S(m) = (2m - 1)s ...................... [1]
は明らかである。
つまり、mが1つ増加すると、S(m)は2つ分増加する。
次に、m番目の三角形と(m+1)番目の三角形との間に存在する三角形を、ここでK番目までの三角形と呼ぶことにする。
K番目までの三角形の右辺を含めた全体の三角形の面積をS(k)とする。
すると、
S(k) = S(m) + s= 2m*s .................. [2]
S(m + 1) = S(k) + s= (2m + 1)s .................. [3]
は明らかである。
m番目までの三角形とk番目までの三角形は斜辺の長さのみが異なる。
底辺は同一の長さb(m)である。
したがって、適当に定数C(=sin(Θ)
:但しΘは斜辺aと底辺bとの仰角)を仮定すれば、
S(m) = C*a(m)*b(m) .................... [4]
S(k) = C*a(k)*b(m) .................... [5]
[1][2]を用いて、[3][4]を解くと、
a(m)/(2m - 1) = a(k)/2m ............... [6]
実は、a(k)とはa(m+1)と同じ長さである。
また、k番目までの三角形と(m+1)番目までの三角形を比べてみると、底辺bのみが異なる。
斜辺は同一の長さa(k)である。
したがって、
S(k) = C*a(k)*b(m) .................... [5-2]
S(m+1) = C*a(k)*b(m+1) ................ [7]
[2][3]を用いて、[5-2][7]を解くと、
b(m)/2m = b(m+1)/(2m+1) ............... [8]
[8]より、b(2) = b(1)*3/2
したがって、”2番目の三角形”の底辺の長さf(2)は、
f(2)
= b(2) - b(1)
= b(1)*1/2
= f(1)*1/2
答え:(2)の辺の長さは(1)の辺の長さの1/2倍。
【問題2】
長さが(1)の辺の4分の1以下になるのは、何番目の辺からでしょうか。
( )の中に入る番号を答えてください。
[8]より、
b(m) = b(1)*{1*3*5*...*(2m-1)}/{2*4*...*(2m-2)}
m番目の三角形の底辺の長さf(m)は、
f(m)
= b(m) - b(m-1)
= b(1)*{1*3*5*...*(2m-1)}/{2*4*...*(2m-2)} -b(1)*{1*3*5*...*(2m-3)}/{2*4*...*(2m-4)}
= b(1)*{1*3*5*...*(2m-3)}*{(2m-1) - (2m-2)}/{2*4*...*(2m-2)}
= f(1)*{1*3*5*...*(2m-3)}/{2*4*...*(2m-2)} .......................[9]
ここで、
f(2)/f(1) = 1/2
f(3)/f(1) = {1*3}/{2*4}= 3/8
f(4)/f(1) = {1*3*5}/{2*4*6}= 5/16
f(5)/f(1) = {1*3*5*7}/{2*4*6*8}= 35/128
f(6)/f(1) = 63/256 < 1/4
答え:(6)番目の三角形の辺から
【問題3】
N番目の辺の長さ((N)の辺の長さ)は、(1)の辺の長さの何倍でしょうか。
[9]より。
答え:{1*3*5*...*(2m-3)}/{2*4*...*(2m-2)} 倍
◆ 問題へもどる
◆ 今週の問題へ