仧峀搰導丂kazaruss 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俠偺憗偝傪俠m/暘偲偡傞偲丄
俙偲俠偼丄俀侽昩偱侾廃偡傞丅
俛偲俠偼丄俀俀昩偱侾廃偡傞丅
俉侽亊俀侽亄俀侽俠亖俇俆亊俀俀亄俀俀俠丂嘆
偙傟傪夝偄偰丄俠亖俉俆m/暘
亂栤戣俀亃
俠亖俉俆m/暘傪嘆偵戙擖偟偰
俉侽亊俀侽亄俉俆亊俀侽亖俁俁侽侽m
亂栤戣俁亃
俛偲俠偑侾侽夞栚偵弌夛偆偺偼
俀俀昩亊侾侽亖俀俀侽昩屻
俉俆亊俀俀侽乛俁俁侽侽亖俆丏俇俇俇俇
傛偭偰俠偼俇廃栚
俠偑侾侽廃偡傞偲
俁俁侽侽亊侾侽乛俉俆亖俁俉俉丏乧昩
俛偲俠偼丄俀俀昩偱侾夞弌夛偆偐傜
俁俉俉乛俀俀亖侾俈丏乧
傛偭偰侾俈夞
亂栤戣係亃
偲傝偁偊偢俙偑俛偵嵎傪偮偗傞偺偼侾暘娫偵侾俆倣
侾廃嵎傪晅偗偰捛偄偮偔偺偼
俁俁侽侽乛侾俆亖俀俀侽暘
偙偺帪偪傚偆偳俠傕摨偠抧揰偵偄傞丅
嵟屻偺栤戣丂俇俇侽暘屻
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俠偺懍偝傪冊乮倣乛暘乯偲偡傞丅
戣堄傛傝
乮俉侽亄冊乯亊俀侽亖乮俇俆亄冊乯亊俀俀
冊亖俉俆
丂摎偊丂俉俆倣乛暘丅
亂栤戣俀亃
乮俉侽亄俉俆乯亊俀侽亖俁俁侽侽
丂摎偊丂俁俁侽侽倣丅
亂栤戣俁亃
僀乯
俠偺懍偝丗俛偺懍偝亖俉俆丗俇俆亖侾俈丗侾俁
侾俈偲侾俁偼屳偄偵慺偱偁傞丅侾俈亄侾俁亖俁侽丅
俠偲俛偼俁侽屄強偱弌夛偆丅
俀俀暘偛偲偵弌夛偆偺偱偁傞偐傜丄侾侽夞弌夛偆傑偱偺帪娫偼丄
俀俀亊侾侽亖俀俀侽乮暘乯
偦偺娫偵俠偺曕偔嫍棧偼丄
俉俆亊俀俀侽亖侾俉俈侽侽乮倣乯
堦廃偑俁俁侽侽倣偱偁傞偐傜丄
侾俉俈侽侽亐俁俁侽侽亖俆丏丏丏俀俀侽侽
偟偨偑偭偰俇廃栚偲側傞丅
丂摎偊丂俇廃栚丅
儘乯
俁俁侽侽亊侾侽亖俁俁侽侽侽乮倣乯
俁俁侽侽侽亐俉俆亖俇俇侽侽乛侾俈乮暘乯
乮俇俇侽侽乛侾俈乯亐俀俀亖俁侽侽乛侾俈亖侾俈亄侾侾乛侾俈
傑偩廳暋偡傞偙偲偼側偄丅
丂摎偊丂侾俈夞丅
亂栤戣係亃
僀乯
A丄B丄C偑摨帪偵弌夛偆偲偄偆偙偲偼丄
A偲B丄A偲C丄B偲C偑弌夛偆偙偲偑摨帪偵婲偙傞偲偄偆偙偲偱偁傞丅
A偲B偑弌夛偆偺偵梫偡傞帪娫
丂俁俁侽侽亐乮俉侽亅俇俆乯亖俀俀侽乮暘乯
B偲C偑弌夛偆偺偵梫偡傞帪娫丂俀俀乮暘乯
C偲A偑弌夛偆偺偵梫偡傞帪娫丂俀侽乮暘乯
俀俀侽丆俀俀丆俀侽偺嵟彫岞攞悢偼丄俀俀侽偱偁傞丅
丂摎偊丂俀俀侽暘丅
儘乯
A偺懍偝丗B偺懍偝亖俉侽丗俇俆亖侾俇丗侾俁
侾俇偲侾俁偼屳偄偵慺偱偁傝丄摨偠曽岦偵曕偄偰偄傞偐傜丄
A偲B偺弌夛偆屄強乮弌敪揰傪娷傔傞乯偼丄
侾俇亅侾俁亖俁丅
A偲B偑俁夞栚偵夛偆屄強偼弌敪揰偲側傞丅
俀俀侽亊俁亖俇俇侽乮暘乯丂俇俇侽暘偼侾侾帪娫偱偁傞丅
僀乯偐傜C傕栠偭偰偄傞偙偲偑傢偐傞丅
丂摎偊丂侾侾帪娫丅
弌夛偆屄強偼廃偺嫍棧偵娭學側偔丄偦傟偧傟偺懍偝偺斾偲曽岦偱寛傑傞偺偱偡偹丅
乽嶼悢偵僠儍儗儞僕乿偱妛廗偟傑偟偨丅
仧搶嫗搒丂Asami 偝傫偐傜偺夝摎丅
20暘屻偵俙俛娫偼300倣棧傟偰偄傞丅
300亐俀亖150(倣乛暘)偙傟偑丄俛偲俠偺懍偝偺榓丅
傛偭偰俠偺懍偝偼85(倣乛暘)
丂丂乧乧乧亂栤戣侾亃
抮偺廃傝偺挿偝偼
20暘亊(俙,俠偺懍偝偺榓)亖3300倣
丂丂乧乧乧亂栤戣俀亃
俛,俠偑侾夞栚偵弌崌偆応強
丂仺丂僗僞乕僩偐傜嵍夞傝偵1870倣偺埵抲
俛,俠偑10夞栚偵弌崌偆応強
丂仺丂僗僞乕僩偐傜嵍夞傝偵18700倣偺埵抲
廬偭偰18700亐3300亖5.6丒丒丒偩偐傜丄
俛,俠偑10夞栚偵弌崌偆偺偼丄俠偑俇廃栚
丂乧乧乧亂栤戣俁亃偵擖偭偨偲偒丅
俠偑10廃偟偨偲偒丄嫍棧偼33000倣恑傫偱偄傞丅
33000亐1870亖17.6丒丒丒偩偐傜丄17夞弌崌偭偰偄傞
丂丂乧乧乧亂栤戣俁亃
俠,俙,俛偑弌崌偆佁俠,俙偑弌崌偆偐偮俠,俛偑弌崌偆丅
俠,俙偑弌崌偆偺偼嵍夞傝偵1700倣偍偒偱偁傝丄
俠,俛偑弌崌偆偺偼嵍夞傝偵1870倣偍偒偱偁傞丅
1700冊亖1870倷佁10冊亖11倷偲側傞嵟彫夝冊傪扵偦偆両
冊亖11
偮傑傝丄俠偑11夞丄俙偲弌崌偊偽椙偔偰丄
20亊11亖220暘屻偵3恖偑弶傔偰弌崌偆
丂丂乧乧乧亂栤戣係亃
傑偨丄偙偺抧揰偼丄俠偑11亊1700亖18700倣懄偪
18700亐3300亖5梋傝2200倣偺抧揰丅
2200傪壗攞偐偟偰偄偭偰丄弶傔偰3300偱妱傝愗傟傞傕偺傪扵偡偲丄
2200亊3偺偲偒偱偁傞偙偲偑暘偐傞偺偱丄3恖偑僗僞乕僩抧揰偵栠傞偺偼
220亊3亖660暘屻乧乧乧亂栤戣係亃
亂暿夝亃丗傾僯儊傪尒傟偽丄
丂亂栤戣俁亃偼俇廃栚,17夞偲丄
丂亂栤戣係亃偼220暘,660暘偲傢偐傞丅
仧愇愳導丂暯揷丂榓峅 偝傫偐傜偺夝摎丅
亂栤戣侾亃偺夝摎
俠偑弌敪偟偰偐傜20暘屻偵俙偲弌夛偄丄偝傜偵2暘屻偵俛偲弌夛偆偺偱丄
俙偺20暘屻偵恑傫偩嫍棧偼1600倣偱丄俛偺22暘屻偵恑傫偩嫍棧偼1430倣偱丄
偙偺娫偺嫍棧偺嵎170倣傪俠偼2暘偱憱傞偺偱
媮傔傞俠偺懍偝偼170/2亖85(倣/暘)偱偡丅
亂栤戣俀亃偺夝摎
俙偲俠偑弶傔偰弌夛偆抧揰傑偱俙偑恑傫偩嫍棧偼
80*20亖1600倣偱丄偙偺娫(20暘娫)俠偑恑傫偩嫍棧偼(栤戣侾夝摎傛傝)
85*20亖1700倣偱丄椉曽偺崌寁偑抮偺廃偺挿偝偵側傞偺偱
媮傔傞廃偺挿偝偼1600+1700亖3300倣偱偡丅
亂栤戣俁亃偺夝摎
傑偢丄戣堄傛傝俛偲俠偑嵟弶偵弌夛偆偺偼22暘屻側偺偱偦傟偧傟
俛偐傜65*22亖1430倣丄俠偐傜85*22亖1870倣丂偺抧揰偱偡丅
(崌寁偑1430+1870亖3300倣偲側傝抮偺廃偵摍偟偄帠偵拲堄偡傞丅)
抮偺廃傪慄暘偵峀偘偰昞偡偲壓恾偺傛偆偵側傝傑偡丅
(壓恾偺偆偪#偼弌夛偆抧揰偱偡丅)
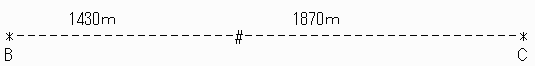
俀夞栚偵弌夛偆偺偼俛偑偝傜偵(22暘娫)1430倣恑傫偩抧揰偵側傝傑偡丅
偙偺偲偒丄俠偼
1430+440亖1870倣(偝傜偵22暘娫)恑傫偱偄傑偡丅
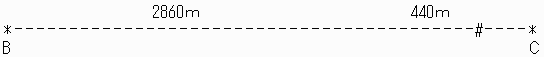
俁夞栚偵弌夛偆偺偼俛偑偝傜偵(22暘娫)1430倣恑傫偩抧揰偵側傝傑偡丅
梫偡傞偵俛偑俠抧揰傑偱峴偭偰偝傜偵嵞傃俛抧揰偐傜990倣恑傫偩抧揰偵側傝傑偡丅
(偙偺娫俛偼440+990亖1430倣恑傒丄俠偼1870倣(2860-990亖1870)恑傒傑偡丅)
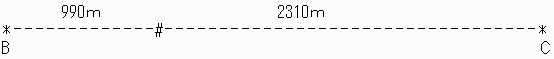
埲壓摨條偵峫偊傟偽傛偄偺偱偡偑丄偙傟傪幃偱昞偡偲丄
侾夞栚偵弌夛偆偺偼
B亖1430*1-(3300*0)亖1430-0亖1430
C亖1870*1-(3300*0)亖1870-0亖1870
B+C亖1430+1870亖3300
俀夞栚偵弌夛偆偺偼
B亖1430*2-(3300*0)亖2860-0亖2860
C亖1870*2-(3300*1)亖3740-3300亖440
B+C亖2860+440亖3300
俁夞栚偵弌夛偆偺偼
B亖1430*3-(3300*1)亖4290-3300亖990
C亖1870*3-(3300-1)亖5610-3300亖2310
B+C=990+2310亖3300
係夞栚偵弌夛偆偺偼
B亖1430*4-(3300*1)亖5720-3300亖2420
C亖1870*4-(3300*2)亖7480-6600亖880
B+C亖2420+880亖3300
丂丂丒
丂丂丒
丂丂丒
侾侽夞栚偵弌夛偆偺偼
B亖1430*10-(3300*4)亖14300-13200亖1100
C亖1870*10-(3300*5)亖18700-16500亖2200
B+C亖1100+2200亖3300
偲側傞偺偱忋婰C偺幃偺拞偺3300*5傛傝C偼6廃傔偲側傝傑偡丅
傑偨C偑10廃偡傞娫偵弌夛偆夞悢偼
3300*9亝1870*仜亙3300*10傪枮偨偡嵟戝偺仜傪媮傔傞偲丄
仜亖17偲側傝傑偡丅
幚嵺丄
1870*17-(3300*9)亖31790亅29700亖2090
1870*18-(3300*10)亖33660亅33000亖660偲側傝傑偡丅
廬偭偰丄B偲C偼17夞弌夛偄傑偡丅
亂栤戣係亃偺夝摎
傑偢A偲B偑弌夛偆偺偼丄B偑廃夞抶傟偲側傞応崌側偺偱丄
3300/(80-65)亖3300/15亖220丂
220暘娫偵堦搙偢偮弌夛偄傑偡丅
B偲C偼栤戣俁偺夝摎夁掱傛傝22暘娫偵堦搙弌夛偄傑偡丅
傛偭偰丄A偲B偲C偑弌夛偆偺偼丄220偲22偺嵟彫岞攞悢偱220暘屻偲側傝傑偡丅
傑偨俁幰偑僗僞乕僩抧揰偱弌夛偆偺偼220暘娫妘偱恑傫偩嫍棧偑3300偱妱傝愗傟傞偲偒側偺偱
A偑220暘娫偱恑傫偩嫍棧偼80*220亖17600丂偲側傝丄
偙偺攞悢偑3300偱妱傝愗傟傞偲偒側偺偱
80*220亖8*10*2*110亖16*1100丂偐偮丂
16偼3偱妱傝愗傟側偄偺偱
3300/1100亖3
80*220*3亖16*1100*3亖16*3300
廬偭偰
220*3亖660暘屻偵俁幰偑僗僞乕僩抧揰偱弌夛偄傑偡丅
(姶憐)
栤戣侾丆俀偲栤戣俁埲崀偺擄堈搙偺僊儍僢僾偑寖偟偄偲巚偄傑偡丅
栤戣俁偼摿偵擄偟偄偐偭偨偱偡丅
栤戣係偼栤戣俁偑偱偒傟偽偱偒傞偱偟傚偆丅
彫妛惗偼帪娫撪偵夝偗傞偺偱偟傚偆偐丄
巹偼愄彫妛峑偺帪偵廗偭偨慄暘恾傪壗搙傕彂偒捈偟偰偙偺摎偊偵偨偳傝偮偒傑偟偨丅
仧撊栘導偺彫妛惗丂俵亅慞斖 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俠偺曕偔懍偝丂俉俆乮倣乛暘乯
俙偺恑傫偩嫍棧丂俉侽亊俀侽亖侾俇侽侽乮倣乯
俛偺恑傫偩嫍棧丂俇俆亊俀俀亖侾係俁侽乮倣乯
侾俇侽侽亅侾係俁亖侾俈侽乮倣乯
侾俈侽亐俀亖俉俆乮倣乛暘乯
亂栤戣俀亃
抮偺廃傝偺挿偝丂丂俁俁侽侽乮倣乯
俙偺恑傫偩嫍棧亄俠偺恑傫偩嫍棧
丂俉侽亊俀侽亄俉俆亊俀侽亖侾俇侽侽亄侾俈侽侽亖俁俁侽侽乮倣乯丂
亂栤戣俁亃
俛偲俠偑侾侽夞栚偵弌夛偆偺偼丂俇廃栚
俠偑俛偵弌夛偆傑偱偺嫍棧偼
丂俉俆亊俀俀亖侾俉俈侽乮倣乯
侾侽夞弌夛偆偐傜
丂侾俉俈侽亊侾侽亐俁俁侽侽亖俆丏俇俇丒丒丒
傑偨丄俠偑侾侽廃偡傞娫偵俛偲俠偼侾俈夞弌夛偆
俁俁侽侽亊侾侽亐侾俉俈侽亖侾俈丏俇係俈丒丒丒
亂栤戣係亃
俁恖偑摨帪偵弌夛偆偺偼丂俀俀侽暘屻
俙偑俛偵捛偄偮偔帪娫傪峫偊傞
俙偼俛偵侾暘偱侾俆乮倣乯嵎傪偮偗傞偐傜丂抮偺廃傝侾廃偟偰捛偄偮偔偵偼
俁俁侽侽亐侾俆亖俀俀侽乮暘乯
乮偙偺帪娫偑俛偲弌夛偆帪娫偱偁傟偽傛偄乯
俠偼俛偲偼俀俀暘偛偲偵弌夛偆偐傜
俀俀侽亐俀俀亖侾侽丂偲側傝侾侽夞栚偵弌夛偆
傑偨丂俁恖偑摨帪偵弌敪偟偰僗僞乕僩偵栠偭偰偔傞帪娫丂俇俇侽暘
俙乮俁恖偺偆偪扤偱傕傛偄乯偑俀俀侽暘偱恑傓嫍棧乮俀俀侽暘屻偲偵俁恖偑弌夛偆偐傜乯偲俁俁侽侽乮倣乯偺嵟彫岞攞悢傪媮傔俙偺懍偝偱妱傞
俉侽亊俀俀侽亖侾俈俇侽侽偲俁俁侽侽偺嵟彫岞攞悢偼俆俀俉侽侽偲側傝
俆俀俉侽侽亐俉侽亖俇俇侽乮暘乯丂
仧晉嶳導丂偄偔傑傞 偝傫偐傜偺夝摎丅
亂栤戣侾丄俀亃
偁傑傝婥偺棙偄偨夝摎偑巚偄晅偐側偄偺偱丄慺捈偵楢棫曽掱幃傪棫偰偰傒傞丅
C偺懍偝傪v[m/暘]丄抮偺廃傝偺挿偝傪L[m]偲偍偔丅
僗僞乕僩偟偰偐傜弶傔偰弌夛偆偲偒丄擇恖偺憱偭偨嫍棧偺榓偼抮偺廃傝偺挿偝偲摍偟偔側傞偺偱丄
80亊20 + v亊20 = L 乨(1)
65亊22 + v亊22 = L 乨(2)
(1)-(2)傪惍棟偟偰丄
80亊20 - 65亊22 = 2亊v
(側傞傎偳丄A偵夛偭偨屻偐傜丄B偵夛偆傑偱偺2暘娫偵恑傓嫍棧偵拲栚偡傟偽椙偄傢偗偱偡偹丅)
v=85,L=3300
傛偭偰丄C偺懍偝偼85m/暘丄抮偺廃傝偺挿偝偼3300m丅
亂栤戣俁亃
B偲C偑10夞栚偵弌夛偭偨偲偒丄擇恖偺恑傫偩嫍棧偺榓偼抮偺廃傝偺挿偝偺10攞偲側傞丅
弌夛偆傑偱偺帪娫傪t1[暘]偲偡傞偲丄
65亊t1 + 85亊t1 = 3300亊10
(65+85)亊t1 = 3300亊10
(僼儉僼儉丄B偲C偺懍偝偺榓偱恑傓恖傪壖掕偡傟偽椙偄傢偗偐丄丄)
t1=220
乮傫?丄B偲C偼22暘偵1夞弌夛偆偐傜丄22暘亊10=220暘偱椙偟偐丅
丂C偑85亊22=1870m憱傞枅偵B偵弌夛偆偺偹丅)
偙偺娫偵C偼
85亊220 = 18700 = 3300亊5 +2200
偡側傢偪丄5廃偲2200m恑傫偱偄傞偙偲偵側傞偺偱丄C偑6廃栚傪憱偭偰偄傞偲偒丅
C偼丄1870m憱傞枅偵B偵弌夛偆偺偱丄10廃恑傓娫偵B偵弌夛偆夞悢偼丄
3300亊10 = 1870亊17 +1210
傛傝17夞丅
亂栤戣係亃
C偼20暘偵1夞A偲弌夛偆丅
傑偨C偼22暘偵1夞B偲弌夛偆丅
傛偭偰20偲22偺嵟彫岞攞悢丄偡側傢偪220暘偵1夞丄A偲B偵摨帪偵弌夛偆丅
弶傔偰3恖偑摨帪偵弌夛偆偺偼丄弌敪偟偰偐傜220暘屻丅
C偼3300/85=660/17暘偱抮偺廃傝傪堦廃偡傞丅
m亊660/17 = n亊220
傪枮偨偡嵟彫偺(m,n)偺慻傪媮傔傞偲m=17,n=3丅
傛偭偰僗僞乕僩偟偰偐傜弶傔偰僗僞乕僩抧揰偱3恖偑弌夛偆偺偼
17亊660/17=3亊220=660暘屻偱偁傞丅
乮偍偄偍偄丄敿擔嬤偔憱傝偭傁側偟偐偄?!)
11,13,17側傫偰偄偆戝偒側慺悢傪場悢偵帩偮悢偽偐傝偑弌尰偟偰丄偪傚偭偲堄抧埆偱偡偹丅
栤戣1,2偼曽掱幃傪棫偰偰夝偄偰偟傑偊偽壗偲傕側偄栤戣偱偡偑丄彫妛惗偑擺摼偱偒傞傛偆側夝摎傪帵偡偺偼堦嬯楯偱偡偹丅
帺怣偑偁傝傑偣傫丅
仧恄撧愳導丂從偒長巕 偝傫偐傜偺夝摎丅
亂栤戣侾丄俀亃
A偺曕偔懍搙傪a丄B偺曕偔懍搙傪倐丄C偺曕偔懍搙傪們偲偡傞丅
傑偨丄抮偺廃傝偺挿偝傪L偲偡傞丅m1,m2傪帺慠悢偲偡傞偲丄埲壓偺摍幃偑惉傝棫偮丅
m1*L = 20 * (a + c) .............(1)
m2*L = 22 * (b + c) .............(2)
栤1偲俀偱偼丄壗廃栚偵弌夛偭偨偐偲偄偆抐傝彂偒偑摿偵側偄偺偱丄侾廃栚偲偡傞丅
偮傑傝丄m1=1,m2=1偲偍偔丅偟偨偑偭偰丄
1.1L = 22 * (a - b)
偙偙偱丄a=80, b=65傪戙擖偟偰丄
L = 3300 (meter)
偙傟傪幃(1)偵戙擖偟偰乮m1=1)丄
c = 85 (meter/min)
摎偊丗
丂們偺曕偔懍搙偼85(meter/min)
丂抮偺廃埻偺挿偝偼丄3300(meter)
亂栤戣俁亅侾亃
B偲C偑堦夞栚偵弌夛偆帪娫偼丄22暘屻偱偁傞丅
偟偨偑偭偰丄10夞栚偵弌夛偆帪娫偼丄
22 * 10 = 220(min)
摎偊丗220暘屻
亂栤戣俁亅俀亃
C偑10廃偡傞傑偱偵丄C偺曕偔偺傋偺嫍棧偼丄
L * 10 = 33000(meter)偱偁傞丅
偙偺嫍棧傪C偑曕偔帪娫偼丄10*L/c(min)偱偁傞丅
B偲C偼22暘偵堦夞弌夛偆偺偱丄慡懱偱弌夛偆夞悢偼丄
10*L/c/22 = 33000/85/22= 17.64丒丒
摎偊丗17夞
亂栤戣係亅侾亃
A偲B偑僗僞乕僩抧揰偐傜弌敪偟偰丄嵞傃弌夛偆帪娫傪T1偲偡傞丅
A偲B偼摨偠曽岦偵堏摦偟偰偄傞偺偱丄嵞傃弌夛偆偲偒偼A偺傎偆偑B傛傝傕侾廃懡偔抮傪夞偭偰偄傞偙偲偵側傞丅
偟偨偑偭偰丄
a*T1 - L = b*T1 ............... (3)
偙傟傪夝偄偰丄
(a - b)*T1 = L
T1= L/(a - b)
丂= 3300/15
丂= 220 (min)
師偵丄A偲C偑弌夛偆傑偱偺帪娫傪T2偲偍偔丅
A偲C偑弌夛偆偙偲偺娭學幃偼(m1,m2傪帺慠悢偲偟偰)丄
m1*L = T2*m2*(a + c)
偙偙偱丄T2*m2偲偼丄(m2)夞栚偵弌夛偆傑偱偺帪娫偲偄偆堄枴偱偁傞偐傜丄
T2*m2= m1*L/(a + c)= 20*m1
偟偐偟側偑傜丄偙偺帪娫偼T1偲偺岞攞悢偱側偗傟偽側傜側偄丅
偟偨偑偭偰丄T1偲偺嵟彫岞攞悢偼m1偑11偺偲偒偱丄
220(min)
摎偊丗220暘屻
亂栤戣係亅俀亃
3恖偑僗僞乕僩偵栠偭偰偔傞帪娫傪T3偲偍偔丅
偡傞偲丄埲壓偺娭學幃偑摫偐傟傞丅
m1*L = a*T3 .............. (4)
m2*L = b*T3 .............. (5)
m3*L = c*T3 .............. (6)
扐偟丄m1,m2,m3偼帺慠悢丅
偟偐偟丄忋偺幃傪夝偔偺偼挿偔側傞偺偱丄栤4-1偺夝摎傪棙梡偡傞丅
3恖偑僗僞乕僩偵栠偭偰偔傞帪娫偼丄3恖偑摨帪偵弌夛偆帪娫T2偺惍悢攞偱偁傝丄A偑堦廃偡傞帪娫偲偺岞攞悢偱偁傞丅
A偑堦廃偡傞帪娫偼丄L/a偱偁傞偐傜丄(m4,m5偼帺慠悢)
m4*L/a = 220*m5
3*m4 = 16*m5
偙偺幃偑帺慠悢m4,m5偱惉棫偡傞偨傔偵偼丄m4=16,m5=3偺偲偒偱偁傞丅
偟偨偑偭偰丄3恖偑僗僞乕僩抧揰偱弌夛偆帪娫偼丄
220*3 = 660(min)
摎偊丗660暘屻
仧戝嶃晎偺崅峑惗丂俠俫俤俠俲 偝傫偐傜偺夝摎丅
亂栤戣侾亃偺夝摎
俀侽暘憱偭偨偲偒丄俙偲俛偺憱偭偨嫍棧偺嵎偼
俀侽亊乮俉侽亅俇俆乯亖俁侽侽倣
俙偲俠偑弌夛偭偰俀暘屻偵俛偑弌夛偭偨偺偱
俁侽侽亐俀亖侾俆侽倣乛暘丒丒丒俛偲俠偺懍偝偺榓
亪侾俆侽亅俇俆亖俉俆倣乛暘
傛偭偰俠偺懍偝偼俉俆倣乛暘
亂栤戣俀亃偺夝摎
俙偲俠偑俀侽暘偱弌夛偭偨偺偱
乮俉俆亄俉侽乯亊俀侽亖俁俁侽侽倣
傛偭偰抮偺傑傢傝偺挿偝偼俁俁侽侽倣
亂栤戣俁亃偺夝摎
俛偲俠偑堦搙偱偁偭偰偐傜師偵弌夛偆傑偱偺帪娫偼
俁俁侽侽亐乮俇俆亄俉俆乯亖俀俀暘丒丒丒嘆
亪侾侽夞栚偵弌夛偆帪娫偼僗僞乕僩偟偰偐傜
俀俀亊侾侽亖俀俀侽暘屻
偦傟傑偱偵俠偑憱偭偨嫍棧偼
俀俀侽亊俉俆亖侾俉俈侽侽倣
侾俉俈侽侽亐俁俁侽侽亖俆梋傝俀俀侽侽
傛偭偰俠偑俛偲侾侽夞夛偭偨偲偒丄俠偼俇廃栚偺偲偒偱偁傞
傑偨丄俠偑侾廃偵偐偐傞帪娫偼俁俁侽侽乛俉俆暘
侾侽廃憱傞偺偱
乮俁俁侽侽乛俉俆乯亊侾侽亖俇俇侽侽乛侾俈暘
嘆傛傝侾俈夞弌夛偆
亂栤戣係亃偺夝摎
俙偑俛偵弶傔偰捛偄偮偔偺偼
俁俁侽侽亐乮俉俆亅俇俆乯亖俀俀侽暘屻
偙偺偲偒丄俙偲俠偼偪傚偆偳侾侾夞栚偵弌夛偆帪娫偱偁傝丄俛偲俠偼侾侽夞栚偵弌夛偆帪娫偱偁傞丅
傛偭偰俀俀侽暘屻偵俙俛俠俁恖偑摨帪偵弌夛偆丅
俙偑侾廃偡傞偺偵偐偐傞帪娫偼俁俁侽侽乛俉侽暘
俛偑侾廃偡傞偺偵偐偐傞帪娫偼俁俁侽侽乛俇俆暘
俠偑侾廃偡傞偺偵偐偐傞帪娫偼俁俁侽侽乛俉俆暘
偙偺俁偮偺嵟彫岞攞悢偼俇俇侽暘
傛偭偰俙俛俠偑僗僞乕僩抧揰偱摨帪偵弌夛偆偺偼俇俇侽暘屻
乮姶憐乯
偣偭偐偔偩偐傜曽掱幃傪巊傢偢嶼悢偱夝偙偆偐偲巚偄丄崱夞偼娙扨偩偐傜偲挷巕偵忔偭偰慡晹夝偄偰傒傑偟偨丅
偔偩傜側偄偙偲偱偡偑丄栤戣係偺摎偊偺俇俇侽暘偭偰丒丒丒丄
侾侾帪娫傕抮偺廃傝憱偭偰壗傗偭偰傫偱偟傚偆偹丄偙偺俁恖偼丅
仧搶嫗搒丂imopy 偝傫偐傜偺夝摎丅
奜廃偺挿偝
L=(80亄冊)亊20亖乮65亄冊乯亊22丂傛傝
冊亖85倣乛暘乮俠偺懍偝乯丆L亖3300倣
22亊10乮夞乯亖220暘丂220亊85亖18700倣
乮6廃栚丗3300亊5亙18700亙3300亊6乯丒丒丒俇廃栚
3300亊10乮廃乯亖33000倣
33000乛俉俆乛俀俀亖17.64丒丒丒
乮17亙17.64丒丒丒亙18乯丒丒丒17夞弌夛偆
22暘乮A偲俠偑弌夛偆昿搙乯偲20暘乮俛偲俠偑弌夛偆昿搙乯偺俴俠俵
丂丒丒丒220暘偑俁恖堦弿偵弌夛偆帪娫
椺偊偽俙偑挌搙尦偵栠傞偺偼3300倣偺攞悢傪挌搙80偱妱傝愗傞忬懺傪峫偊傟偽傛偔丆
165暘屻乮3300亊4倣乯丆
偙傟偲220暘乮3恖偑堦弿偵弌夛偆帪娫乯偺LCM
丂丒丒丒660暘屻偑尦偺応強偱俁恖偑堦弿偵弌夛偆
俛偱峫偊偰傕丆摨條偵660暘屻乮3300亊13倣乯偲220暘偲偺LCM
丂丒丒丒660暘屻偲側傞丅
俠偱峫偊偰傕丆摨條偵660暘屻乮3300亊17倣乯偲220暘偲偺LCM
丂丒丒丒660暘屻偲側傞丅
埲忋丆俠丗85m/暘丄堦廃3300m丄
B偲C偑10夞夛偆偺偼俠偺6廃栚丄
俠偑10廃偡傞娫偵俛偲偼17夞弌夛偆
220暘屻偵嵟弶偵俁恖偑堦弿偵弌夛偄丄
660暘屻偵尦偺応強偱俁恖偑堦弿偵弌夛偆丅
偲偄偭偨偲偙傠偱偟傚偆偐丒丒丒丅
偙傟傪嶼悢偱夝偔偵偼偳偆偟偨傜傛偄偺偱偟傚偆偐丠丠丠
仧嶰廳導丂巺惔孨 偝傫偐傜偺夝摎丅
亂栤戣侾亃丂乮俉俆倣/暘乯
俠偼俀侽暘屻偵俙偲弌夛偭偨丅
偦偺帪揰偱俙偼俉侽亊俀侽亖侾俇侽侽倣恑傫偱偄傞丅
俀俀暘屻偵俛偲弌夛偭偨丅
偦偺帪揰偱俛偼俇俆亊俀俀亖侾係俁侽倣恑傫偱偄傞丅
傛偭偰丄俠偼俙偲弌夛偭偰偐傜俛偲弌夛偆傑偱偺俀暘娫偵丄
侾俇侽侽亅侾係俁侽亖侾俈侽倣恑傫偱偄傞丅
偩偐傜丄俠偺曕偔懍偝偼侾俈侽亐俀亖俉俆倣/暘
亂栤戣俀亃乮俁俁侽侽倣乯
俠偼俙偲弌夛偆傑偱偺俀侽暘娫偱俉俆亊俀侽亖侾俈侽侽倣恑傫偩丅
堦曽俙偼偦偙傑偱偱侾俇侽侽倣恑傫偱偄傞丅
傛偭偰丄抮偺廃傝偺挿偝偼
侾俇侽侽亄侾俈侽侽亖俁俁侽侽倣
亂栤戣俁亃乮俇廃栚丄侾俈夞乯
俛偲俠偼僗僞乕僩偟偰偐傜俀俀暘屻偵弌夛偭偨丅
師偵俀恖偑弌夛偆偺傑偱偵偐偐傞帪娫偼丄偦偙傪僗僞乕僩抧揰偲偟偰俀恖偑曕偒巒傔偨偲峫偊傞偲丄嵟弶偵弌夛偆傑偱偲摨偠俀俀暘丅
偮傑傝丄俀恖偼俀俀暘偛偲偵弌夛偆丅
侾侽夞栚偵弌夛偆偺偼丄俀俀亊侾侽亖俀俀侽暘屻
偦偺帪揰偱俠偼俀俀侽亊俉俆亖侾俉俈侽侽倣恑傫偱偄傞丅
侾俉俈侽侽亐俁俁侽侽亖俆偁傑傝俀俀侽侽
傛偭偰俇廃栚丅
俠偑侾侽廃偡傞偺偵偼丄
俁俁侽侽亊侾侽亐俉俆亖俁俉俉偁傑傝俀侽偱丄俁俉俉暘偲偁偲壗昩偐偐偐傞丅
俀俀暘偛偲偵弌夛偆偺偩偐傜丄俁俉俉亐俀俀亖侾俈偁傑傝侾係
傛偭偰侾俈夞丅
亂栤戣係亃乮俀俀侽暘屻丄俇俇侽暘屻乯
俙偲俠偼俀侽暘丄俛偲俠偼俀俀暘偛偲偵弌夛偆偺偱丄俠偑俙偲俛偵摨帪偵弌夛偆偺偼丄俀侽偲俀俀偺嵟彫岞攞悢偺俀俀侽暘屻丅
俀俀侽暘屻偵俙偼俀俀侽亊俉侽亖侾俈俇侽侽倣恑傫偱偄傞丅
侾俈俇侽侽亐俁俁侽侽亖俆偁傑傝侾侾侽侽側偺偱丄偦偺応強偼僗僞乕僩抧揰偐傜侾侾侽侽倣棧傟偰偄傞丅
俁俁侽侽亐侾侾侽侽亖俁側偺偱丄偙偺俀俀侽暘傪俁夞孞傝曉偣偽俁恖偑僗僞乕僩抧揰偵偦傠偆丅
俀俀侽亊俁亖俇俇侽暘屻
悢妛偺栤戣偵偙偆偄偆僣僢僐儈偼僞僽乕偱偡偑丄俁恖偲傕偡偛偄懱椡偱偡偹偉丅
帺暘偺摎偊偑娫堘偭偰偄傞偺偱偼偲晄埨偵側傝傑偡丅
仧愇愳導丂Takashi 偝傫偐傜偺夝摎丅
佱嘥佲
俀侽暘屻偺俙偺埵抲偼丄俉侽亊俀侽亖侾俇侽侽亂倣亃
俀俀暘屻偺俛偺埵抲偼丄俇俆亊俀俀亖侾係俁侽亂倣亃
偙偺俀恖偵媡夞傝偟偰偄偨俠偑弌夛偆偺偩偐傜丄俠偼俀暘娫偵侾俈侽倣堏摦偟偰偄傞帠偵側傞丅
俉俆亂倣乛暘亃
佱嘦佲
俀侽暘屻偵俙偲俠偑弌夛偆偺偱丄抮偺夞傝偺挿偝俴偼丄
俴亖俉侽亊俀侽亄俉俆亊俀侽
丂亖俁俁侽侽亂倣亃
佱嘨佲
俛偲俠偑嵟弶偵俀俀暘屻偵弌夛偆丅
師偼偦傟偐傜俀俀暘屻偵傑偨弌夛偆丅
偙偺傛偆偵侾侽夞栚偵弌夛偆偺偼丄俀俀侽暘屻偱偁傞丅
俠偺堏摦偟偨憤嫍棧Lc偼丄
Lc亖俉俆亊俀俀侽亖侾俉俈侽侽亂倣亃
侾俉俈侽侽亐俁俁侽侽亖俆丏俇俇俇丒丒丒
傛偭偰丄俠偼俇廃栚偱偁傞丅
傑偨丄俠偑侾侽廃偡傞偺偵偐偐傞帪娫偼丄
俁俁侽侽侽亐俉俆亖俁俉俉丏俀俁俆丒丒丒亂暘亃
俛偲俠偼俀俀暘偛偲偵堦夞弌夛偆偺偩偐傜丄
俁俉俉丏俀俁俆丒丒丒亐俀俀亖侾俈丏俇係俈丒丒丒亂夞亃
傛偭偰丄俛偲俠偼侾俈夞弌夛偆丅
佱嘩佲
俙偲俛偑弌夛偆偙偲傪峫偊傞丅
偙偺擇恖偼丄摨偠岦偒偵傓偐偭偰曕偄偰偄傞偐傜丄擇恖偺埵抲偺偢傟偰偄偔検偼丄
俉侽亅俇俆亖侾俆亂倣乛暘亃
傛偭偰丄擇恖偑摨帪偵弌敪偟偰堦廃懡偔夞偭偰偄傞俙偑俛偵捛偄偮偔偺偵偐偐傞帪娫偼丄
俁俁侽侽亐侾俆亖俀俀侽亂暘亃
偪傚偆偳偙偺帪俛偲俠傕侾侽夞栚偵弌夛偆偐傜丄俁恖偑摨帪偵弌夛偆丅
俀俀侽亂暘亃
傑偨丄俀俀侽暘屻俙偺埵抲偼丄
俉侽亊俀俀侽亖侾俈俇侽侽亂倣亃偩偐傜俆廃偲侾侾侽侽倣抧揰偱偁傞丅
傛偭偰俇俇侽暘屻偵側傞偲丄俙偺埵抲偼丄
乮俉侽亊俇俇侽乯亐俁俁侽侽亖侾俇亂廃亃偟偨僗僞乕僩抧揰偵側傞丅
偙偺帪丄俁恖偼偪傚偆偳俁夞栚偵弌夛偆偐傜丄俁恖偑僗僞乕僩抧揰偱弌夛偆偺偼丄
俇俇侽亂暘亃
仧暉壀導丂拞嶳 偝傫偐傜偺夝摎丅
乽栤戣侾乿
20暘屻偺A偺堏摦嫍棧丂丂80亊20亖1600[m]
B偺堏摦嫍棧丂丂65亊20亖1300[m]
C偺懍偝傪x偲偡傞偲丂丂(1600-1300)亐(65亄x)亖2
x亖85
丂摎偊丂85 m/暘
乽栤戣俀乿
A偲C偑20暘屻偵弌崌偆偙偲偐傜
80亊20亄85亊20亖3300
丂摎偊丂3300 m
乽栤戣俁乿
10夞栚偵弌崌偆傑偱偵C偑恑傓嫍棧偼
85亊(22亊10)亖18700[m]
傛偭偰丂丂18700亐3300亖5.6丒丒丒
丂摎偊丂6廃栚
C偑10廃偡傞偺偵梫偡傞帪娫偼
丂丂(3300亊10)亐85[m]
B偲C偑弌崌偆夞悢偼
丂丂{(3300亊10)亐85}亐22亖17.6丒丒丒
丂摎偊丂17夞
乽栤戣係乿
3恖摨帪偵弌崌偆偵偼丄AC偺弌崌偄偲BC偺弌崌偄偑摨帪偵婲偙傟偽傛偄偐傜丄20[暘屻]偲22[暘屻]偺嵟彫岞攞悢傪媮傔傞
丂摎偊丂220暘屻
3恖偑僗僞乕僩偱弌崌偆偵偼丄A偺僗僞乕僩捠夁偲丄ABC偺弌崌偄偑摨帪偵婲偙傟偽傛偄偐傜丄3300/80[暘屻]偲220[暘屻]偺嵟彫岞攞悢丠傪媮傔傞
丂摎偊丂660暘屻
仧挿嶈導丂Dr. Berserker 偝傫偐傜偺夝摎丅
亂栤戣侾亃
堦師曽掱幃偱夝偄偰傒傑偟傚偆丅
俠偑曕偄偨摴偺傝偲丄俙傑偨偼俛偑曕偄偨摴偺傝偺榓偼丄偳偪傜傕偪傚偆偳抮偺廃傝堦廃偲偄偆偙偲偵側傝傑偡偹丅
偡偄傑偣傫丅俠偲丄俙傑偨偼俛偑弌夛偭偨偲偒偺偍偼側偟丅
偙偙偱丄俠偺曕偔懍偝傪倃偲偍偔偲丄抮偺廃傝偺挿偝偼師偺俀捠傝偵偁傜傢偣傑偡丅
俀侽倃亄俀侽丒俉侽
乮俀侽亄俀乯倃亄乮俀侽亄俀乯丒俇俆
偙傟偼偳偪傜傕抮偺廃傝堦廃偺挿偝側偺偱丄偙偺擇偮偺幃偺抣偼摨偠偲偄偆偙偲偵側傝傑偡丅
偟偨偑偭偰丄
俀侽倃亄侾俇侽侽亖俀俀倃亄侾係俁侽
偙傟傪偲偔偲丄倃亖俉俆
傛偭偰丄俠偺曕偔懍偝偼丄枅昩俉俆儊乕僩儖偲偄偆偙偲偑傢偐傝傑偟偨丅
亂栤戣俀亃
愭偺夝摎偑暘偐偭偰偄偨偩偗傟偽丄偁偲偼娙扨偱偡偹丅
忋偺偳偪傜偐偺幃偵丄倃亖俉俆傪戙擖偟偰偄偨偩偄偰丄
俁俁侽侽偲偄偆悢偑弌偰偔傞偺偱丄俁俁侽侽儊乕僩儖偑摎偊偵側傝傑偡丅
亂栤戣俁亃
師偼俛偲俠偱偡偹丅
俛偲俠偑慜偵弌夛偭偰偐傜丄師偵弌夛偆傑偱丄俀俀暘偯偮偐偐傝傑偡丅
偲偄偆偙偲偼丄俛偲俠偑侾侽夞栚偵弌夛偆偺偼丄
俀俀亊侾侽=俀俀侽暘屻偲偄偆偙偲偵側傝傑偡丅
偙偺娫偵丄俠偼丄俉俆亊俀俀侽=侾俉俈侽侽儊乕僩儖曕偄偨偙偲偵側傝傑偡丅
抮偺廃偺挿偝偼丄俁俁侽侽儊乕僩儖偲偄偆偙偲偑暘偐偭偰偄傞偺偱丄
侾俉俈侽侽亐俁俁侽侽=俆+俀/俁丄偮傑傝丄俇廃栚傪夞偭偰偄傞搑拞偵側傞傫偱偡偹丅
師偵丄俠偑侾侽廃夞傞偲偒偵丄俛偲俠偼丄壗夞弌夛偆偐偲偄偆偙偲偱偡偑丄俛偲俠偑慜偵弌夛偭偰偐傜丄師偵弌夛偆傑偱丄俀俀暘丄
偮傑傝丄偙偺娫偵俠偼丄俀俀亊俉俆=侾俉俈侽儊乕僩儖曕偄偨偙偲偵側傝傑偡丅
傑偨丄俠偑侾侽廃偡傞偨傔偵曕偐側偗傟偽側傜側偄摴偺傝偼丄
俁俁侽侽亊侾侽=俁俁侽侽侽儊乕僩儖丅偟偨偑偭偰丄
俁俁侽侽侽亐侾俉俈侽亖侾俈亄侾侾乛侾俈
偮傑傝丄侾俈夞弌夛偭偰偐傜丄侾侽廃曕偒廔傢傞偲偄偆偙偲偵側傝傑偡丅
亂栤戣係亃
俁恖偑摨帪偵弌夛偆偲偒丄俠偼丄俙偲俛偺椉曽偲弌夛偭偰偄傞偙偲偵側傝傑偡丅
乽摨帪偵乿偑億僀儞僩偲側傝傑偡偑丄偙傟偼丄俙偲俠偑弌夛偆帪娫娫妘俀侽暘偲俛偲俠偑弌夛偆帪娫娫妘俀俀暘偺嵟彫岞攞悢偲偄偆偙偲偵側傝傑偡丅
偙傟偼丄俀俀侽側偺偱丄俀俀侽暘屻偑摎偊偵側傝傑偡丅
偝傜偵俁恖偑僗僞乕僩抧揰偱摨帪偵弌夛偆偨傔偵偼丄俁恖偑摨帪偵弌夛偆偺偼俀俀侽暘偛偲側偺偱丄偙偺娫偵曕偄偨摴偺傝偑丄抮偺廃偺挿偝丄俁俁侽侽儊乕僩儖偺攞悢偵側偭偰偄傟偽偄偄偲偄偆偙偲偵側傝傑偡丅
俠傪婎弨偵偟偰峫偊偰傒傑偟傚偆丅俠偼俀俀侽暘枅偵丄
俀俀侽亊俉俆亖侾俉俈侽侽儊乕僩儖
曕偄偰偄傞偺偱丄偙偺攞悢偑俁俁侽侽偺攞悢偱偁傟偽偄偄偲偄偆偙偲偵側傝傑偡丅
偟偨偑偭偰丄俁俁侽侽偲侾俉俈侽侽偺嵟彫岞攞悢丄俆俇侾侽侽
偮傑傝俠偑俆俇侾侽侽儊乕僩儖曕偄偰弶傔偰丄俁恖偑摨帪偵丄僗僞乕僩抧揰偱弌夛偆偺偱偁偭偰丄偙偙傑偱偐偐傞帪娫偼丄
俆俇侾侽侽亐俉俆亖俇俇侽
偮傑傝丄俇俇侽暘偐偐傞傢偗偱丄偙傟偼傛乕偡傞偵侾侾帪娫偲偄偆偙偲偵側傝傑偡偹丅
丒丒丒晛捠丄侾侾帪娫傕曕偔偱偟傚偆偐偲偄偆嵟戝偺栤戣偑偁傝傑偡偑丅
偁偲丄捛媮偡傋偒偱偼側偄偺偱偡偑丄捠忢丄恖娫偺曕偔懍偝偼丄係Km/h偲偄偆晽偵尵傢傟偰偄傞偙偲偼桳柤偱偡偑丄寁嶼偟偰傒傑偟偨丅
俙丗俁丆俋Km/h
俛丗係丆俉Km/h
俠丗俆丆侾Km/h
偐側傝憗偄偱偡偹偉丅晛捠偺戝恖偑寉偔僕儑僊儞僌偡傞偔傜偄偺懍偝偼偁傝傑偡傛丅
傕偟偙偺俁恖偺愝掕偑彫妛惗偩偲偟偨傜丒丒丒丅
偙傢乣偄丒丒丒丅
丂仧丂栤戣傊傕偳傞
丂仧丂崱廡偺栤戣傊
丂丂