『今週の問題』第25回　解答

◆石川県　平田　和弘 さんからの解答。

【問題１】の解答

次の正方形の面積は前の正方形の面積の２倍になります。
(小学生ならば、正方形を一番最初の正方形の半分の大きさの三角形に分解するとわかります。)
(中学生ならば、次の正方形が前の正方形の対角線を１辺とする正方形であること
(×＝２)からもわかります。)

また正方形が重なる部分の面積はそれぞれ前の正方形の面積の1/2ずつで、かつ正方形が重なる部分はお互いに重ならないので、求める面積は

　(１＋２＋４＋８)−(1/2＋１＋２)
＝１２−0.5
＝11.5ｃｍ²です。

【問題２】の解答

問題１と同様に考えて

　(１＋２＋４＋８＋１６)−(1/2＋１＋２＋４)
＝２４−0.5
＝23.5　ｃｍ²です。

【問題３】の解答

正方形の数が７までは正方形が重なる部分はお互いに重ならないのですが、８以上になると再度重なります。

正方形の数	正方形が再度重なる 部分の面積
８	１×1/2＝1/2
９	２×1/2＝１
１０	４×1/2＝２
１１	８×1/2＝４
・ ・	・ ・

となるので、面積は

(１＋２＋４＋８＋１６＋３２＋６４＋１２８＋２５６＋５１２＋１０２４) 
　−(1/2＋１＋２＋４＋８＋１６＋３２＋６４＋１２８＋２５６)
　−(1/2＋１＋２＋４)

【おまけ】の解答

ｎ≦７のときは

正方形ｎ個の面積の総和は
1+2+2²+2³+.........+2^n-1＝2ⁿ-1　で

重なっている部分の面積の総和は

　1/2+1+2+........+2^n-3
＝1/2{1+2+2²+........+2^n-2}
＝1/2{2^n-1-1}　

なので求める面積は

　(2ⁿ-1)-1/2{2^n-1-1}
＝2ⁿ-2^n-2-1/2　ｃｍ²・・・・・・・(A)です。

ｎ≧８のときは

上記(A)−{1/2+1+2+2²+......+2^n-9}
となるので、式の後半を計算すると

　−{1/2+1+2+2²+......+2^n-9}
＝-1/2{1+2+2²+........+2^n-8}
＝−{2^n-8−1/2}　

となるので求める面積は、

　{2ⁿ-2^n-2-1/2}−{2^n-8−1/2}
＝2ⁿ-2^n-2-2^n-8　ｃｍ²　・・・・・・・(B)です。

実際に上記問題1〜3に適用してみると
問題1のとき　n≦７　なので

　2⁴-2^4-2-1/2
＝16-4-1/2
＝11.5

問題2のとき　n≦７　なので

　2⁵-2^5-2-1/2
＝32-8-1/2
＝23.5

問題3のとき　n≧８　なので

2¹¹-2^11-2-2^11-8
＝8(16×16-8×8-1)
＝1528

となって上記と一致します。

◆広島県　清川　育男 さんからの解答。

【問題１】

答え　１１．５ｃｍ²

【問題２】

答え　２３．５ｃｍ²

【問題３】

答え　１５２８ｃｍ²

ヒントのわなにきずきました。
S(n)=1+1.5×(2^n-1-1)　と思ったのですが、９個目で３６０度回転して、１０個目から元の面積から減じることになるのですね。

Ｎ番目の正方形の面積A(n)は、A(n)=2^n-1

１１番目までの面積の和は、５番目から１１番目までの面積の和に等しい。

 16+32×(3/4)+64×(3/4)+128×(3/4)+256×(3/4)+512×(3/4)+1024×(3/4)

答え　１５２８ｃｍ²

S(n)=1+1.5×(2^n-1-1)
T(11)=S(11)-S(4)+A(4)×(1/2)=1524+4=1528

◆海外　西野　友朗 さんからの解答。

【問題１】

１．題意に従うと、新しい正方形は前の正方形に対して面積が２倍、位置は前の正方形のある頂点(この頂点は不動)を中心に45度時計回りに回転した位置に描かれることになります。

この時、新しい正方形はその面積の1/4が前の正方形と重なっているので、原則として面積の増分は、新しい正方形の面積の3/4になります
(「原則として」の部分については、3.で後述)。

２．便宜上nつ目(nは自然数)の正方形を描いたときの、求める図形の面積をS(n)とします。
上記を元に7つ目までの正方形について考察します。

正方形 の数n	新しい正方 形の面積	面積の増分	面積合計 S(n)
１	1=20	1	1
２	2=21	1.5=3/4x21	2.5
３	4=22	3 =3/4x22	5.5
４	8=23	6 =3/4x23	11.5
５	16=24	12 =3/4x24	23.5
６	32=25	24 =3/4x25	47.5
７	64=26	48 =3/4x26	95.5

上記から、S(n)は階差数列が初項1.5、項比2の等比数列であり、自身の初項が1である数列であると言えるので：

n=1,...,7のとき、
S(n)=0.75x(2ⁿ)-0.5 ......(☆1)

と表現できます(補足1参照)。

３．さて7つ目の正方形を描くと、この正方形は1つ目の正方形から見て270度(=45度x6)回転して、丁度1つ目の正方形に接します。
8つ目の正方形からは面積の増分を考える際に、1.の原則の増分から、前に描いた正方形に重なる分を差し引く必要があります
(これを以下「修正分」と呼ぶことにします)。

(HPの実験でNo.=8を実行してみるとイメージできますが)、8つ目の正方形を描くと、ちょうど1つ目の正方形の半分が修正分にあたることが分かりますので：

正方形 の数n	新しい正方 形の面積	面積の増分	面積「修正」分	面積合計 S(n)
１	1=20	1		1
・・・・・・ (省略) ・・・・・・
７	64=26	48=3/4x26		95.5
８	128=27	96=3/4x27	-0.5=-1/2x20	191

9つ目以降を考えると：

正方形 の数n	新しい正方 形の面積	面積の増分	面積「修正」分	面積合計 S(n)
９	256=28	192=3/4x28	-1 =-1/2x21	382
10	512=29	384=3/4x29	-2 =-1/2x22	764
11	1024=210	768=3/4x210	-4 =-1/2x23	1528

n個目の正方形は、丁度(n-7)個目の正方形の半分と重なるので：

正方形 の数n	新しい正方 形の面積	面積の増分	面積「修正」分	面積合計 S(n)
ｎ	2n-1	3/4x2n-1	-1/2x2n-8	191x2n-8 ↑(推測)

４．上記の推測が一般に成り立つことは、数学的帰納法を用いて確認することが確認できます
　(補足2参照)。 ......(☆2)

以上(☆1,2)をまとめると、nを自然数として：

n=1,...,7のとき S(n)=0.75x(2ⁿ)-0.5

n=8以上のとき S(n)=191x2^n-8 [完]

[補足1]

階差数列 C(n)=S(n+1)-S(n)を定義すると、

C(n)=1.5x2^n-1、
ΣC(n)=1.5x(2ⁿ-1)

n=2以上のとき、

S(n)=1+ΣC(n-1)
　=1+1.5x{2^n-1-1}
　=0.75x(2ⁿ)-0.5

この式は S(1)=1も成り立っているので、(☆1)の様に表現する。 [完]

[補足2]

n=8以上のとき、S(n+1)=2xS(n)、
一般項としては191x2^n-8となることの証明

i) n=8の場合、上記の計算より
　S(9)=382=2xS(8)=191x2^9-8 となり成立。

ii)n=k (ただし、kは8以上)の場合に成立すると仮定すると：

S(k)=191x2^k-8

このとき、n=k+1の場合を考えると：

よって、n=k+1の場合にも成立する。

iii) i)とii)より、8以上の全ての場合について成立。 [完]

【問題１】　11.5
【問題２】　23.5
【問題３】　1528
【おまけの問題】　上記の通り

◆福岡県　中山 さんからの解答。

【問題１】

正方形４個分の面積から、重なっている部分の面積を引く

(1＋2＋4＋8)−(1/2＋1＋2)＝11.5

答え　11.5cm²

【問題２】

正方形５個分の面積から、重なっている部分の面積を引く

(1＋2＋4＋8＋16)−(1/2＋1＋2＋4)＝23.5

答え　23.5cm²

【問題３】

正方形１１個分の面積から、重なっている部分の面積と、前の周回と重なる部分の面積を引く　

　(1＋2＋4＋8＋16＋32＋64＋128＋256＋512＋1024)
−(1/2＋1＋2＋4＋8＋16＋32＋64＋128＋256)
−(1/2＋1＋2＋4)
＝1528

答え　1528cm²

◆富山県　いくまる さんからの解答。

正方形をn個描いたときの図形をD(n)、
その面積をS(n)ｃｍ²とする。（単位省略）

i)1≦n≦7のとき。

点SよりD(n)の各頂点に直線を引くと(n+1)個の直角二等辺三角形に分けられる。
それぞれの面積は1/2,1,…,(1/2)×2^n-1 および、(1/2)×2^n-1がもう一つ。
よって

S(n)=(1/2)×20 + (1/2)×21 + … +(1/2)×2n-1 + (1/2)×2n-1

S(n)=3×2^n-2 - 1/2

ii)n≧8のとき。

8個以上の正方形を描くときには前に書いた正方形との重なりができるが、新しくできるD(n)はすべてD(7)と相似である。
D(n-1)とD(n)の相似比は１:であるから、

S(n)=2×S(n-1)

i)よりD(7)=191/2であるから、

S(n)=191×2^n-8

以上より

i)1≦n≦7のとき ：S(n)=3×2^n-2 - 1/2
ii)n≧8のとき ：S(n)=191×2^n-8

◆石川県　Takashi さんからの解答。

２≦ｎ≦７のとき、ｎ個目の正方形を書くとｎ−１個目の正方形の半分に重なる。
よって、全体の面積Ｓ(n)は、

　Ｓ(n)
＝Ｓ(n-1)＋２^n-1−0.5×２^n-2
＝Ｓ(n-1)＋３×２^n-3

Ｓ(n)＝0.75×２ⁿ−0.5　【１≦ｎ≦７】

(1)ｎ＝４のとき、
　Ｓ(4)＝１１．５

(2)ｎ＝５のとき、
　Ｓ(5)＝２３．５

ｎ≧８のとき、ｎ個目の正方形を書くと、ｎ−１個目とｎ−７個目の正方形のそれぞれ半分に重なる。

よって、

　Ｓ(n)
＝Ｓ(n-1)＋２^n-1−0.5×２^n-2−0.5×２^n-8
＝Ｓ(n-1)＋95.5×２^n-8

　Ｓ(n)
＝Ｓ(７)＋95.5×｛２^n-7−１｝
＝１９１×２^n-8

(3)ｎ＝１１のとき、
　Ｓ(11)＝１５２８

(おまけ)

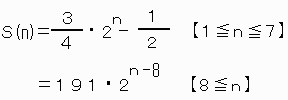
◆京都府　みなみようへい さんからの解答。

ｎ個目の正方形の面積：S(n)＝2^n-1

2≦ｎ≦7のとき

S(1)＋(3／4)｛S(2)＋…＋S(n)｝
＝3×2^n-2−1／2

これはｎ＝1のときも成立

8≦ｎのとき

S(1)＋3／4｛S(2)＋…＋S(ｎ)｝−(1／2)｛S(1)＋…＋S(n−7)｝
＝191×2^n-8

以上をまとめて

1≦ｎ≦7のとき　3×2^n-2−1／2

8≦ｎのとき　　 191×2^n-8

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる。