『今週の問題』第24回　解答

◆広島県　清川　育男 さんからの解答。

【問題１】

答え
１個，２個，４個，６個，９個，１２個，１６個，２０個。

【問題２】

答え
　１５個のとき　１６ｍ
　１６個のとき　１６ｍ
　１７個のとき　１８ｍ
　１８個のとき　１８ｍ。

【問題３】

４０個のとき、周の長さは２６ｍ。

答え　３７個，３８個，３９個，４１個，４２個。

【おまけの問題】

プログラムを組んでシミュレーションしました。
元の位置をＸーＹ座標の(０，０)とする。３０万歩まで。

　１回目　　　　４８２歩。
　２回目　　　　４８８歩。
　３回目　　　４６７０歩。
　４回目　２６０５０６歩。
　５回目　２６１８４２歩。
　６回目　２６１８４４歩。
　７回目　２６１８９０歩。
　８回目　２６１８９２歩。
　９回目　２６１９０２歩。
１０回目　２６２１４４歩。
１１回目　２６２６２６歩。
１２回目　２６２６３２歩。
１３回目　２６６８１４歩。　　
３０万歩　(１３０，−２１６)

◆石川県　平田　和弘 さんからの解答。

【問題１】の解答

図形が長方形(正方形)になるには、スタートしてからまず左に進むので必ず
縦の長さ≦横の長さ　 ・・・(１)という関係が成り立ち、

しかも縦の長さと横の長さの関係は

縦の長さ＝横の長さ　　　・・・(２)
　　(この場合は正方形)　

または

縦の長さ＝横の長さ−１　・・・(３)
　　(この場合は長方形)

のどちらかが成り立つ場合だけです。

従って考えられる組み合わせは

縦	横	塗った個数
１	１	１
１	２	２
２	２	４
２	３	６
３	３	９
３	４	１２
４	４	１６
４	５	２０

の８通りです。

答えは　
１，２，４，６，９，１２，１６，２０　です。

【問題２】の解答

図形の周の長さは例えば塗った個数が１５のときでも１６でも変わらない。
(要するに角がへこんでいてもいなくても変わらない。)
また４×４(＝１６個)の正方形より一つでも塗った個数が多くなると次の長方形(この場合４×５＝２０個)まで周が同じことに目をつけて、周の長さを以下のように分類できます。

塗った個数	基本となるもの (これと同じという意味)		縦×横	周の長さ
１	１	→	１×１	４
２	２	→	１×２	６
３〜４	４	→	２×２	８
５〜６	６	→	２×３	１０
７〜９	９	→	３×３	１２
１０〜１２	１２	→	３×４	１４
１３〜１６	１６	→	４×４	１６
１７〜２０	２０	→	４×５	１８
・・・	・・・	→	・・・

となるので求める答えは

１５個のとき　１６ｍ
１６個のとき　１６ｍ
１７個のとき　１８ｍ
１８個のとき　１８ｍです。

【問題３】の解答

問題２と同様に考えて

塗った個数	基本となるもの (これと同じという意味)		縦×横	周の長さ
・・・	・・・	→	・・・
２１〜２５	２５	→	５×５	２０
２６〜３０	３０	→	５×６	２２
３１〜３６	３６	→	６×６	２４
３７〜４２	４２	→	６×７	２６
・・・	・・・	→	・・・

となるので４０個塗った図形は上記３７〜４２のグループになるので求める答えは
３７，３８，３９，４１，４２です。

(感想)

この問題は最初とりかかりが難しかったが素直に考えてあること(周の長さの規則性や図形の分類方法)等に気がつけばわりと簡単です。
問題１は比較的わかると思うのですが、問題２の本質がわからないと問題３は難しいと思います。
しかし、問題１から３まで順を追って導けるようになっているのでなかなか良問だと思います。
(社会に出てから数学とはあまり縁のない私が申すには恐縮ですが........)

(おまけ解答)

図が書きにくいので説明が難しいのですが、Ａから前後左右どちらにも１/4の確率で移動するので特に前に動く場合について考えます。
(他は角度を90度ずつずらして考えれば同じです。)

　　列     1   2   3   4   5   6   7   8   9   10  11  12  13  14  
行
 1
 2
 3
 4
 5
 6
 7                                 G1
 8                             G7  F1  G7
 9                         G21 F6  E1  F6  G21
10                     G35 F15 E5  D1  E5  F15 G35
11                 G35 F20 E10 D4  C1  D4  E10 F20 G35
12             G21 F15 E10 D6  C3  B1  C3  D6  E10 F15 G21
13 　 　　 G7　F6　E5　D4　C3　B2　S1　 B2　C3　D4　E5　F6　G7
14　　　　　　　　　　　　　　　　　A
15

同様に、
Cn(n＝1,3)はその地点から最短距離で3コマ進むと元へ戻れます。
nは最短で戻る場合の経路の数を表しています。
(C1の地点から最短距離でAへ戻る経路の数は1で、C3の地点から最短距離でAへ戻る経路の数は3です。
(そういう地点であるという意味です。))

以下同様に考えると上の図のようになります。
(上の図では例えばF1およびF6の位置はこのようになって、それ以外のものは例えばE10とE5にはさまれたAからみて1回り外のもの(F)はF15(＝10+5)という関係になっています。)

1コマで戻れるのはS1の地点(1通り)だけでその確率は1/4です。

2コマで戻れるのはB1,B2,B2の3地点で合計5(2×2+1)通りで、このように戻ってこられる確率は
それぞれ1/4×1/4＝1/16です。

3コマで戻れるのはC1,C3,C3,C3,C3の5地点で合計13(3×4+1)通りで、このように戻ってこられる確率は
それぞれ1/4×1/4×1/4＝1/64です。

以下同様に考えて、またそれぞれ独立して試行されるので求める確率は

1/4+{(1/4)2×(2×2+1)}+{(1/4)3×(3×4+1)}+{(1/4)4×(4×4+6×2+1)}+・・・(Ｓ)　

しかし実際に計算してみると

第1項までの和は　1/4＝0.25
第2項までの和は　9/16＝0.5625
第3項までの和は　49/64＝0.765625...
第4項までの和は　225/256＝0.8789062...
第5項までの和は　961/1024＝0.9384765625.....
第6項までの和は　3969/4096＝0.9689941.....
第7項までの和は　16129/16384＝0.984436......

となって1に近づくことがわかります。
従って試行回数を無限に近づけると元の地点Ａに戻ってこられる確率は１に近づきます。
要するに元に戻ってこられるようになります。
(実際に収束するかどうかの判定や、収束値は予測の世界です。)

(感想)

とりあえずこんな風にしか考えられませんでした。
数列の等比数列を駆使してできるのでしょうか。
まったくわかりませんでした。
(その方向へ走ったら深みにはまりました。)

直感で考えると元へ戻れなさそうな気がしますが、実際はまったく反対であるという事実には驚かされます。

(おまけ解答の追補)

調べた結果、この問題は２次元のランダム・ウォークの問題であり、解答はかなり困難です。
(証明はあるのですが理解がとても困難です。現役で確率論をやっているのなら話は別でしょうが)
とはいえ結果を申しますと、やはり元に戻る確率は無限回試行すると１になるようです。

[概略]

この問題はポイヤ(G.Polya)の定理とよばれ、

(定理)

１次元および２次元の対象なランダム・ウォークでは、粒子が遅かれ早かれ(したがって無限回)、初めの位置に戻る確率は１である。
しかし３次元の場合は、その確率はおよそ０．３５にすぎない。

(証明の概略)

２次元の場合は地点Ａを原点とし、ｘ軸、ｙ軸に平行に正または負の方向へそれぞれ１ずつ移動すると考える。
このとき、最初の位置への復帰の確率はｘ軸、ｙ軸への正の方向への回数がそれぞれ負の方向への回数に等しいときに限り可能である。

Ｕ(n)をｎ回めの試行で最初の位置に達する確率とすると、
ｎ＝奇数とすると、Ｕ(n)＝０　(奇数回の試行では戻れない！)

ｎ＝偶数(簡単のために２ｎ)とすると
(２ｎ回中ｋ回右へｋ回左へ行き、(ｎ−ｋ)回上へ(ｎ−ｋ)回下へくる確率Ｕ(２ｎ)は)

多項分布により

となります。
この無限和が発散することを証明すればよいようです。・・・(※参照)

(1)式

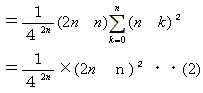
但し、

(2n　n)＝

2n(2n-1)・・・・(n+1) ―――――――――――――― 1×2×・・・・×(n-1)×n

とする。

ここでスターリングの公式

により

∞ Σ n＝0

U(2n)

は発散するそうです。(※ここがさっぱりわかりません。)

(証明終わり)

(※)
一般に事象εが起こるのが一時的である

⇔

u＝

∞ Σ j＝0

U(j)が有限

(⇔は必要十分条件という意味で、U(j)はj回めの試行でεが起こる確率とする。)

◆奈良県　岸本　大和 さんからの解答。

【問題１】

1. 縦の長さを ａ 横の長さ を ｂ とする(ａ、ｂは自然数)と、長方形(正方形含む)の桝目の数(面積)は、ａ × ｂと書ける。

2. 塗りつぶし方が渦巻き状に中からなので、ａ と ｂ の差は２ 以上にならない。
   また、最初に進む方向が横だから ｂ≧a 。
   つまりａ＝ｂ または ｂ＝ａ＋１。

3. １，２から長方形は
   ａ×ａの形か、ａ×(ａ＋１)＝ａ×ａ＋ａ の形になっている。

4. また、周囲の長さは、長方形の状態から次の一つを塗りつぶした時、２だけ増加し、次の長方形になるまで変わらない。

5. ３から ａ を １〜１０とすると、次の表ができる。

ａ	1	2	3	4	5	6	7	8	9	10
ａ×ａ	1	4	9	16	25	36	49	64	81	100
ａ×ａ＋ａ	2	6	12	20	30	42	56	72	90	110

これより 問題１の解答は
１ ２ ４ ６ ９ １２ １６ ２０

【問題２】

周囲の長さは、５の表から、１５〜１８前後を取り出し、４の考え方で整理する。
長方形である、桝目１２の時は ２×(４＋３)なので、問題２の解答は、次の通り。

マス目の数	12	13	14	15	16	17	18	19	20	21
周囲の長さ	14	16	16	16	16	18	18	18	18	20

【問題３】

５の表から、桝目４０ よりすぐ上の長方形をみると、４２。
４の性質から、桝目(３６＋１)から４２までは、周囲の長さが同じ。
つまり、桝目３７ ３８ ３９ ４１ ４２ が ４０と周囲の長さを持つ。

◆福岡県　中山 さんからの解答。

【問題１】

n×n、n×(n＋1)、(n＋1)×(n＋1)の順番で長方形(正方形)になることから考える。

答え　1、2、4、6、9、12、16、20個

【問題２】

15個塗った時の図形は、16個(4×4)の形から1個分とれた形なので周の長さは16個の時と同じ。
17個および18個塗った時の図形は、16個の形に付け加えた形であることから考える。

答え

　15、16個の時、周の長さ16
　17、18個の時、周の長さ18

【問題３】

長方形(正方形)に1個分付け加えた形から、次の長方形(正方形)に至るまでの間周の長さは一定であることから考える。

答え　37、38、39、41、42個の時

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる。