『今週の問題』第231回　解答

◆東京都　明　さんからの解答

【問題１】

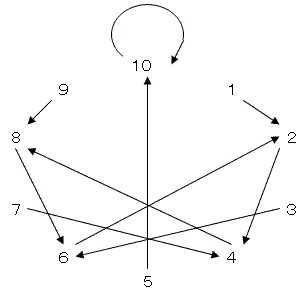
駒の移動を図で表すと下記の通りとなります。



図をたどれば、“４”からスタートし、５回目は“８”になります。

【問題２】

スタートが“３”の場合、１回目に“６”になり、以後６→２→４→８　のループを回って、４回ごとに“６”に戻ります。
１＋４×１２=４９回で“６”に戻るので、５０回目は“２”です。

【問題３】

６→２→４→８　のループの外から駒が入ってくる場合を考えます。
“６”の１回前は“３”、２回前は“９”、３回前は“７”、４回前は“１”で、これ以外はループの中に駒があります。
２００７=４×５０１＋３　ですので、“６”の２００７回前は、３回前と同じ位置に駒があります。

したがって、考えられるすべての駒の位置は　“７”と“２”です。

【おまけ１】

ｎ回目の駒の位置は　２n（ｍｏｄ　Ｐ）　となります。
Ｐは素数なので、フェルマーの定理から　２P-1 =１　（ｍｏｄ　Ｐ）
で　Ｐ-１回目には“１”に戻ります。

【おまけ２】

２n（ｍｏｄ　Ｐ）が　ｎ=Ｐ-１　で始めて１となる（２がＰの原始根となる）場合を求めることになります。
計算機で始めの方を調べた結果です。

3 　5  11  13  19  29  37  53  59  61 
67 　83  101  107  131  139  149  163  173  179 
181 　197  211  227  269  293  317  347  349  373 
379 　389  419  421  443  461  467  491  509  523 
541 　547  557  563  587  613  619  653  659  661 
677 　701  709  757  773  787  797  821  827  829 
853 　859  877  883  907  941  947  1019  1061  1091
以上

◆神奈川県　Gaku　さんからの解答

【問題１】

"8"

以下、自己満足な説明（初等整数論の知識は仮定しないが、それなりの理解力は仮定する）
駒を動かすことはカードの数を2倍することと考えられる。
例えば、"3"にある駒は3よりもさらに3大きい数である6に動く。
このとき、カードは1の位だけを表していると考えて、13や23は"3"のカードが表しているとする。
例えば、"7"にある駒は7よりも7大きい数である14に動くが、14は"4"のカードが表しているから、"4"に動く。

こう考えると、問題は次のように書き換えられる。
「4を2倍する操作を5回繰り返したとき、1の位は何ですか。」

1の位だけを比べたときにnとmが等しくなることを、
n≡m(mod 10)と書く。

●n≡m(mod 10)であるということは、n-mが10で割れるということと同値である。

証明

nとmの1の位をそれぞれk、lとすると、n=10n'+k、m=10m'+lと書ける。
n-m=10(n'-m')+(k-l)
kとlは一桁の数だから、k-lは-10よりも大きく10よりも小さい。
したがって、n-mが10で割れるということは、k-lが0ということと同値で、これは、n≡m(mod 10)と同値である。

●n≡n'(mod 10)、m≡m'(mod 10)ならば、
n*m≡n'*m'(mod 10)となる。

証明

n≡n'(mod 10)とm≡m'(mod 10)より、n-n'とm-m'は10で割れる。
したがって、
n*m-n'*m'=(n-n')*m+(m-m')*n'も10で割れるから、n*m≡n'*m'(mod 10)である。



これを用いると、問題は
「4*25≡n(mod 10)となるような1以上10以下のnは何ですか。」
と書き換えられる。

ここで、

24＝16≡6(mod 10)
2*6＝12≡2(mod 10)
4*6＝24≡4(mod 10)
6*6＝36≡6(mod 10)
8*6＝48≡8(mod 10)
10*6＝60≡10(mod 10)

より、nが偶数でiが自然数のとき、
n*24*i≡n*6i≡n(mod 10)
（6を5で割った余りが1であることを考えればもっと簡単にわかることだが…）

よって、解答は、
4*25＝4*2*24≡4*2＝8(mod 10)

【問題２】

"2"

3*250＝3*22*24*12≡3*22＝12≡2(mod 10)

【問題３】

"2"または"7"

22007＝23*24*501≡23≡8(mod 10)
n*8≡6(mod 10)
となるような1以上10以下のnは2と7である。
（nを5で割った余りが2になるから…）

【おまけ１】

pが2でないときは"1"、pが2のときは"2"
pが2のときは明らかに"2"のカードに止まる。

pが2でないときは、pと2は互いに素だから、フェルマーの小定理より、
2p-1≡1(mod p)

【おまけ２】

2,（3,5,11,13…）

pが2でないときは0回目に1に止まっているので、
『（Ｐ−１）回目にはじめて「おまけ１の答えのカード」に止まる』
という問題ならば、解答は2のみであるが、これでは未解決問題にならないので、1回以上の移動を行ったときだけを考える。

pについて、n回目にはじめて"1"に止まるとする。
このとき、nは、2n≡1(mod p)となる最小のもの、すなわち、2の位数である。

2の位数がp-1であるような環Z/pZを探せばよい。

【感想】

おまけ２、よく分かりません。整数論は難しいですね。

◆兵庫県　せらふぃっく　さんからの解答

【問題１】

集合A={1,2,3,4,5,6,7,8,9,10}

関数fを f:A→Aで

f(1)=f(6)=2,f(2)=f(7)=4,f(3)=f(8)=6,f(4)=f(9)=8,f(5)=f(10)=10

と定義する。

求める駒の位置は(fffff)(4)[五回合成する]で表わされるので、求める駒の位置は8

【問題２】

関数の定義の仕方から、はじめに3の位置にあるときは、8にあるときと同じ結果となる。

また偶数の場合は、4回合成すると元の位置に戻ってくるので、
50=4*12+2より、 求める駒の位置は、f(f(8))で表わされるので、求める駒の位置は2

【問題３】

前問の結果から、2007を4で割ったあまりが3なので3回合成すると6となる自然数を求めればよい。
関数の定義の仕方から求める駒の位置は、2と7

◆千葉県　DMR　さんからの解答

※ココでは一般性を持たせるために漸化式と合同式を用いた回答にしました。

まず，最初に駒のある位置を，添え字を用いてa[1]と表す。
ここで，a[2]を１回駒を動かした位置。a[i]を(i-1)回駒を動かした位置とする。

さて，問題より，a[n+1] ≡ 2a[n](mod 10) が分かる。これより，
a[n] ≡ a[1] * 2n-1 (mod 10).

これは底が10でなくても同様に成り立つ。

すなわち，円周上に並べられた1, 2, ・・・ pのカードは，自然数の集合Ｎのpによる剰余類の代表元と捉えることができるのだが，カードを一直線上に1,2,・・・p,1,2,・・・p・・・と際限なく並べたとすると，
a[n+1] = 2*a[n]が成り立つ。

これより，任意の自然数pについて，
a[n] ≡ a[1] * 2n-1 (mod p)

これより，

問題１の解答は，
　4*25　＝27＝128より，「８」のカード。

問題２の解答は，
　3*250 ≡3*24*12 +2 ≡3*22≡2 (mod 10)より，「２」のカード。

問題３の解答は，
　A*22007 ≡ 6 (mod 10)を解いて得られるAの値。

すなわち，2007 = 4 * 501 + 3より，
A*22007 ≡A*23≡8A≡6(mod 10)

これを満足するAの値は，A=2, 7である。
よって，「２」と「７」のカード。

おまけ１にもちょっとチャレンジします。
大学２年生なので未解決とか言われると構えてしまうのですが，構わずやらせていただきます。

上で考察したとおり，(P-1)回目には， 2p-1をpで割った余りが答えになる。
すなわちフェルマーの小定理より，Pが奇素数ならば，「１」のカードに。P=2ならば「２」のカードに止まる。

◆岐阜県の高校生　de-go　さんからの解答

一度10に置かれると、何回繰り返してもまた10に戻る
2→4→8→6と繰り返す

【問題１】

4→8→6→2→4→8となるので、答えは8

【問題２】

最初は3で、次から6→2→4→8→6と繰り返す

50/4=12あまり2 より
6→2→4→8→6を12回繰り返し、残りの2回は最初の3→6と最後の6→2となる

よって2にとまる

【問題３】

最後に6に止まることから逆に考えると
最後は6→2→4→8→6で終わることになる

これを何回か繰り返しているかは
2007/4=501あまり3 より501回繰り返していることがわかる

残りの3回で6になるためには、ローテーションから、1回の操作で4にならなければならないので、答えは、 2 又は 7 となる

◆宮城県　だいもん　さんからの解答

【問題１】

最初に置いた駒の目が n だとすると、それに自身の数を足すという操作は、自身を２倍することに等しく、
m回その操作を繰り返した後の目は、n×2mの下一桁に相当する。

以上のことから、4×25 = 4×32 = 128。 ∴8

【問題２】

2n = {2,4,8,16,32,64,128・・・}からもわかるように、2nの下一桁はn mod 4に等しい。
即ち、250の下一桁は4であり、今数xの下一桁を出力する関数をs(x)と定義すれば、
s(3×250) = 2。

∴2

【問題３】

最初の数を n （1≦n≦10）とすれば、s(n×22007) = 6を満たすnを求めることになる。
2007 mod 4 = 3であるから、下一桁が8となるため、
結局s(8n) = 6を満たす n を求めればよい。

∴n = 2,7

自分にとっては非常に解きやすい物でした。modの考え方は循環系にとって強力ですね！

【おまけ１】

この円を一種のP進数と考えることも出来るから、問題と同様の考え方をした後に、mod Pを行えば答えは導出される。
故に、この場合は、1×2P-1 mod Pである。

【おまけ２】

題意により、求めるべきは1×2P-1 = P-1
（但し、途中に出てくるすべての数１,2,・・・,2P-2は(P-1)で割ったあまりが(P-1)ではない）

例えば、P=7の時を考えると、この円は実際｛1,2,3,4,5,6,7｝の円であるが、mod演算後の遷移を考え、
7進数と見て、{0,1,2,3,4,5,6}と考えることも出来る。

また、2を越える素数は、全て奇数であるから、
P-1は偶数になるはずであり、整数(P-1)/2が存在する。
その時、素数PがP-1に辿り着く条件は、P+(P-1)/2=2kを満たすような整数kが存在すればよいが、これだけではP-1回目に”はじめて”辿り着くことにはならない。
（この場合は２周目に辿り着く条件である）

また、メルセンヌ型素数pについては、log2(P+1)回目において、あまりが1になるため、そこで循環し、永遠にP-1には辿り着かない。

◆愛知県　RIT　さんからの解答

(1)は普通に最初に4から数えると、
1回目8→2回目6→3回目2→4回目4→5回目8 となるので、答えは8です。

【問題２】

最初に3に置いて数えてみると、3回目で4にとまります。

次に問題１に着目すると、一回4からスタートすると必ずそれから4回後には4に戻るので、あとは8、6、2、4、8、6…と規則的に続きます。
つまり、1回目6→2回目2→3回目4→4回目8→5回目6→6回目2…と続きます。

これは4回周期で繰り返すので、□回目の□を4で割った余りによって、□回目の時どのカードにとまるかが決められます。

実際この場合は4で割った余りが1ならば6、2ならば2、3ならば4、0ならば8のカードの上にいます。
50÷4＝12余り2なので、答えは2のカードです。

【問題３】

まず1〜10のカードの上に最初に駒を置くと、何回目で初めて4のカードの上に来るかを数えてみます。

すると、1は2回目、2は1回目、3は3回目、4は4回目、6は2回目、7は1回目、8は3回目、9は4回目です。

5は、1回目に10のカードの上に行き、1回10のカードの上に乗ると、もうあとは10→10→10…と繰り返してしまうので、絶対4のカードの上には乗りません。
同様にして最初に10に駒を乗せても、4には行き着きません。

あとは(2)の時と同様に、余りを調べればいいですが、2007÷4＝501余り3なので、(2)の結果より最初に3に駒を置くのでは、2007回目には4のカードの上にいて、6のカードの上にはいません。
8も3と同様3回目に4のカードの上にくるので2007回目には4のカードの上にいて、6のカードの上にはいません。

最初に1に乗せた場合は、□回目に駒が乗っているカードの番号は、□÷4の余りが2ならば4、3ならば8、0ならば6、1ならば2なので、これも同様に2007回目には8のカードの上にいて、6のカードの上にはいません。

また自動的に最初に6のカードに乗せたときも違ってくることになります。

最初に4に乗せた場合も、□回目に駒が乗っているカードの番号は、□÷4の余りが0ならば4、1ならば8、2ならば6、3ならば2となるので、2007回目には2のカードの上に乗っているので、6のカードの上にはいません。

自動的に最初に9のカードに乗せたときも違ってきます。

最初に2のカードに乗せた場合だと、□回目に駒が乗っているカードの番号は、□÷4の余りが1ならば4、2ならば8、3ならば6、0ならば2なので、ちゃんと2007回目には6のカードの上にいます。

よって自動的に7のカードに最初に乗せた場合も2007回目には6のカードの上にいることになります。

よって最初は2か7のカードの上に駒を置いたことになります。

◆福島県　Alembert　さんからの解答

【準備】

本稿では、記号 [n] で、n と書かれたカードを表すものとする。

まず、[2] に駒を置いた場合、駒は ([2]→)[4]→[8]→[6]→[2] と移動する。
つまり、4 回目で元に戻る。
これは、駒が [2] から始めて 4 周期で移動することを意味する。
これを、状態(1) と呼ぶ。

[10] に駒をおいた場合、駒は [10] から移動しなくなる。
これを、状態(2) と呼ぶ。

[5], [10] というカード以外に駒を置くと、駒は有限回で状態 (1) へ遷移する。
実際、駒の初期位置と、最初に状態 (1) に遷移する（[2] に移動する）回の関係は、表 1 のようになる。

（表1）
初期位置回
１１
２０
３２
４３
６１
７４
８２
９３

なお、[5], [10] というカードに駒を置いた場合は、駒は有限回で状態 (2) へ遷移する。

【問題１】

駒の移動は、次のようになる。
　[4]→[8]→[6]→[2]→[4]→[8]

答え：[8]

【問題２】

　表1 より、最初に [3] に駒を置くと、駒は 2 回目ではじめて状態 (1) へ遷移することがわかる。
つまり、問題は、「最初に [2] に駒を置くと、駒は 48 回目にどのカードに止まるか」という問題に帰着される。

状態 (1) では、駒は 4 周期で移動するから、48 回目の駒の位置は、48 を 4 で割った余り、すなわち 0 回目の駒の位置と一致する。
これは [2] である。

答え：[2]

【問題３】

駒が 2007 回目で [6] に止まったということは、2008 回目では [2] に止まる。
まず、[5] と [10] は明らかに除外できる。
それ以外のカードに駒を置いた場合は、表1 より、4 回以下の操作で状態 (1) へ遷移する。

従って、2008 回目はすでに状態 (1) であると考えられる。
2008 を周期 4 で割った余りは 0 であるから、2008 回目で [2] に移動するには、
(周期 4 の倍数)回目で [2] に駒が移動することが必要である。
（条件を満たさない数、例えば x 回目で [2] に駒が移動したとすると、2008 = n*4 + x を満たすような整数 n が存在しない）

表1 より、これを満たすのは [2] と [7] のみである。

答え：[2]、[7]

【おまけ（準備）】

[P] に駒を置くと、何度操作しても駒は [P] から動かなくなるから、[P] は [0] と等価である。
同様に、n ≡ m (mod P) であるとき、[n] と [m] は等価である。

次に、n 回目の駒の位置の番号を a(n) で表現すると、
問題から、a(n+1) ≡ a(n) + a(n) (mod P) = 2*a(n) が成り立つ。

また、a(0) ≡ 1 (mod P) である。

【おまけ１】

問題は、次のように帰着される。

......　　a(0) ≡ 1 (mod P)
......　　a(n+1) ≡ 2*a(n) (mod P) (n ≧ 0)
......　と定義する。
このとき、a(P-1) を求めよ。

定義から、
　a(n) ≡ 2n (mod P)が成り立つ。

従って、a(P-1) ≡ 2P-1 (mod P)

P は素数であるから、フェルマーの小定理より、
　2P-1 ≡ 1 (mod P)

故に、　a(P-1) ≡ 1 (mod P)

答え：[1]

【おまけ２】

わかりません（ゴメンナサイ…。）
とりあえず、プログラムを作って確かめてみたところ、1 〜 1000 の間では、こんな感じになりました。

2 , 3 , 5 , 11 , 13 , 19 , 29 , 37 , 53 , 59 , 61 , 67 , 83 , 101 , 107 , 131 , 139 , 149 , 163 , 173 , 179 , 181 , 197 , 211 , 227 , 269 , 293 , 317 , 347 , 349 , 373 , 379 , 389 , 419 , 421 , 443 , 461 , 467 , 491 , 509 , 523 , 541 , 547 , 557 , 563 , 587 , 613 , 619 , 653 , 659 , 661 , 677 , 701 , 709 , 757 , 773 , 787 , 797 , 821 , 827 , 829 , 853 , 859 , 877 , 883 , 907 , 941 , 947

■ソースコード（十進BASIC）

INPUT n
DIM a(n)
LET a(1) = 1

LET m = INT(SQR(n))

! エラトステネスの篩
FOR i=2 TO m
   IF a(i) <> 1 THEN
      LET j = i*2
      DO WHILE j <= n
         LET a(j) = 1
         LET j = j + i
      LOOP
   END IF
NEXT i

! チェック
FOR i=2 TO n
   IF a(i) = 0 THEN
      LET flag = 0
      LET x = 1
      FOR j=1 TO i-2
         LET  x = MOD(x*2, i)
         IF x = 1 THEN
            LET  flag = 1
            EXIT FOR
         END IF
      NEXT j
      IF flag = 0 THEN PRINT i
   END IF
NEXT i

END

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる