◆大阪府 電電虫 さんからの解答
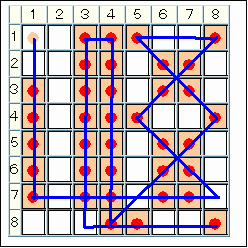
【問題1−1】
スタート(1,1)→
(7,1)→(7,7)→(2,7)→(6,3)→(1,3)→
(1,8)→(8,8)→(8,4)→(2,4)→(2,6)→
(6,6)→
11手
【問題2−1】
同数の連続した整数で表せる条件は
「連続する個数の差の約数の個数の場合である」
例えば
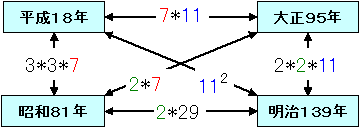
平成x年
昭和x+63年
になるので
63の約数1,3、…、63の場合である。
本題に戻ると
平成x年
昭和x+63年 63=32*7
大正x+77年 77=7*11
明治x+121年 121=112
となるので
●平成を含む場合
公約数は
平成 昭和 大正 7
平成 大正 明治 11
平成 昭和 明治 1
●平成を含まない場合
昭和y年
大正y+14年 14=2*7
明治y+58年 58=2*29
となるので
公約数は
昭和 大正 明治 2
以上より、3つの組合せで、同一の個数の連続した整数の和で表せる年が存在しない場合は
平成 昭和 明治
の組み合わせである。
◆石川県 いくまる さんからの解答
【問題2−1】
3つの年号を例えば、N1, N2, N3とし、ともにp個の連続した整数の和 (pは2以上の自然数)で表せた(*)と仮定すると、
N1 = m1 + (m1 +1) + ... + (m1 + p-1) ...(1)
N2 = m2 + (m2 +1) + ... + (m2 + p-1) ...(2)
N3 = m3 + (m3 +1) + ... + (m3 + p-1) ...(3)
を満たす整数の組 (m1, m2, m3)が存在する。
(2)-(1), (3)-(1)より
N2 - N1 = p (m2 - m1)
N3 - N1 = p (m3 - m1) ...(4)
これらの2組の"2つの年号の差" (すなわちN2 - N1 と N3 - N1)が共通因数pを持つこと(**)が必要条件である。
このときN2 - N1=p*d21, N3 - N1=p*d31とすると(4)の2つの式より
m2 = m1 + d21
m3 = m1 + d31
となり、m1を適当に決定することで(m1, m2, m3)が決定することとなり、連続するp個の整数の和で表すことが可能である。
よって題意(連続する整数の和で表せない)を満たすのは2組の"2つの年号の差"が互いに素となるような3つの年号の組み合わせの場合である。
ところで2つの年号の差は常に一定であり、
(昭和) - (平成) = 63 = 3*3*7
(大正) - (平成) = 77 = 7*11
(明治) - (平成) = 121 = 11*11
(大正) - (昭和) = 14 = 2*7
(明治) - (昭和) = 58 = 2*29
であることから、平成、昭和、明治が題意を満たす年号の組み合わせである。
【感想】
おもしろい問題ですね。
数学の先生方っていつもこんなことを考えながらカレンダーを見たり新聞を読んだりされているのでしょうか(^^)
◆広島県 清川 育男 さんからの解答
【問題1−1】
11手
スタート(1,1)→
(7,1)→(7,6)→(3,6)→(6,3)→(1,3)→
(1,8)→(8,8)→(8,4)→(2,4)→(2,7)→
(7,7)→
【問題1−2】
284通り。
NO. 1 A( 7 , 1 ) A( 7 , 6 ) A( 3 , 6 ) A( 6 , 3 ) A( 1 , 3 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 4 ) A( 2 , 4 ) A( 2 , 7 ) A( 7 , 7 ) NO. 2 A( 7 , 1 ) A( 7 , 6 ) A( 3 , 6 ) A( 6 , 3 ) A( 1 , 3 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 4 ) A( 2 , 4 ) A( 2 , 7 ) A( 8 , 7 ) NO. 3 A( 7 , 1 ) A( 7 , 6 ) A( 2 , 6 ) A( 2 , 4 ) A( 8 , 4 ) A( 8 , 7 ) A( 2 , 7 ) A( 6 , 3 ) A( 1 , 3 ) A( 1 , 8 ) A( 8 , 8 ) NO. 4 A( 7 , 1 ) A( 7 , 6 ) A( 2 , 6 ) A( 2 , 4 ) A( 8 , 4 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 3 ) A( 6 , 3 ) A( 1 , 8 ) A( 8 , 8 ) NO. 5 A( 7 , 1 ) A( 7 , 6 ) A( 2 , 6 ) A( 2 , 4 ) A( 8 , 4 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 3 ) A( 6 , 3 ) A( 2 , 7 ) A( 7 , 7 )以下略。全リストはこちらです。
【問題2−1】
1) A=18 B=81 C=95 |A+C-2*B|=49=7*7 7 個 28 = 1 +・・・+ 7 91 = 10 +・・・+ 16 105 = 12 +・・・+ 18 35 = 2 +・・・+ 8 98 = 11 +・・・+ 17 112 = 13 +・・・+ 19 42 = 3 +・・・+ 9 105 = 12 +・・・+ 18 119 = 14 +・・・+ 20 49 = 4 +・・・+ 10 112 = 13 +・・・+ 19 126 = 15 +・・・+ 21 56 = 5 +・・・+ 11 119 = 14 +・・・+ 20 133 = 16 +・・・+ 22 63 = 6 +・・・+ 12 126 = 15 +・・・+ 21 140 = 17 +・・・+ 23 ----------------------- 2) A=18 B=81 C=139 |A+C-2*B|=5 解なし ----------------------- 3) A=18 B=95 C=139 |A+C-2*B|=33=3*11 11 個 66 = 1 +・・・+ 11 143 = 8 +・・・+ 18 187 = 12 +・・・+ 22 77 = 2 +・・・+ 12 154 = 9 +・・・+ 19 198 = 13 +・・・+ 23 88 = 3 +・・・+ 13 165 = 10 +・・・+ 20 209 = 14 +・・・+ 24 99 = 4 +・・・+ 14 176 = 11 +・・・+ 21 220 = 15 +・・・+ 25 110 = 5 +・・・+ 15 187 = 12 +・・・+ 22 231 = 16 +・・・+ 26 121 = 6 +・・・+ 16 198 = 13 +・・・+ 23 242 = 17 +・・・+ 27 ----------------------- 4) A=81 B=95 C=139 |A+C-2*B|=30=2*3*5 2 個 3 = 1 + 2 17 = 8 + 9 61 = 30 + 31 5 = 2 + 3 19 = 9 + 10 63 = 31 + 32 7 = 3 + 4 21 = 10 + 11 65 = 32 + 33 9 = 4 + 5 23 = 11 + 12 67 = 33 + 34 11 = 5 + 6 25 = 12 + 13 69 = 34 + 35 13 = 6 + 7 27 = 13 + 14 71 = 35 + 363つの数を、a<b<cとする。
(2*x+n-1)*n=2*(a+m)
(2*x+2*(b-a)/n+n-1)=2*(b+m)
(2*x+2*(c-a)/n+n-1)=2*(b+m)
と表される。
(a,b,c)----->(b-a,c-a)
1) (18,81,95)--->(63,77) 公約数は7。
2) (18,81,139)-->(63,121) 互いに素。解なし。
3) (18,95,139)-->(77,44) 公約数は11。
4) (81,95,139)-->(14,44) 公約数は2。
【問題2−2】
7+11 997+1009 23+29 1019+1021 41+43 1033+1039 47+53 1039+1049 53+59 1049+1051 71+73 1063+1069 233+239 1229+1231 239+241 1231+1237 257+263 1249+1259 271+277 1259+1277 293+307 1291+1297 367+373 1361+1367 373+379 1367+1373 461+463 1453+1459 547+557 1543+1549 593+599 1583+1597 607+613 1601+1607 683+691 1669+1693 863+877 1861+1867 1019+1021 2011+2017 1097+1103 2089+2099 1129+1151 2131+2137 1171+1181 2161+2179 1193+1201 2179+2203 1289+1291 2281+2287 1367+1373 2357+2371 1433+1439 2423+2437 1471+1481 2467+2473 1493+1499 2477+2503 1553+1559 2549+2551 1709+1721 2707+2711 1721+1723 2713+2719 1811+1823 2803+2819 1973+1979 2969+2971 2099+2111 3089+3109 2269+2273 3259+3271 2309+2311 3301+3307 2311+2333 3313+3319 2333+2339 3329+3331 2393+2399 3389+3391 2399+2411 3391+3407 2543+2549 3539+3541 2549+2551 3541+3547 2633+2647 3631+3637 2729+2731 3721+3727 2731+2741 3727+3733 3023+3037 4021+4027 3361+3371 4357+4363
◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】 11手
手順は【1−2】解に示す26番であった。

【問題2−1】 平成 昭和 明治 の場合。
∵mから始まるn個の和はnの偶奇性により
| nの倍数ないし | n 2 |
の奇数倍です。 |
◆ 問題へもどる
◆ 今週の問題へ