◆東京都 明 さんからの解答
【問題1】
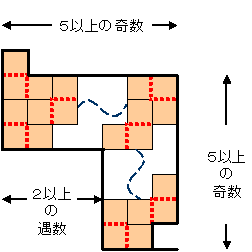
ー ー ー | | ー ー | | | ー ー | | ー ー ー<できるだけ少ないマッチ棒を取り去って長方形をなくするための方針>
まず全体図形の最外周を除いて、マッチ棒でできた図形の内部を、マッチ棒を取り去ってできる多角形(長方形でない)で埋めることを考えます。
多角形に含まれている単位の正方形の数をKとすると、
取り去らなければならないマッチ棒は最低K−1本です。
従って、全体図形を埋めた多角形の数が大きいほど、取り去るマッチ棒の数は少なくて済みます。
このため、出来るだけ小さい多角形で図形の内部を埋めることで、取り去るマッチ棒の数を少なくすることができます。
長方形でない多角形の最小のものは下図の『 状の形です。
ー ー | | ー | | ーこの『 パターンで、しかも『 』の組み合わせ等で長方形ができないように図形の内部を埋めることができれば、取り去るマッチ棒の数を最小にできます。
【問題2】
ー ー ー ー | | | ー ー | | | | ー ー ー | | | | ー ー | | | ー ー ー ー【おまけ1・2】
n×nの場合の長方形の個数を求めます。
n×nの横の境界線と縦の境界線(各 n+1本)に着目します。
任意の一つの長方形(正方形も含む)は、一組の横の2本の境界線と縦の2本の境界線により構成されます。
逆に一組の横の2本の境界線と縦の2本の境界線は唯一つの長方形を構成します。
従って長方形の数は、横のn+1本の境界線から2本を選び、さらに縦のn+1本の境界線から2本を選ぶ場合の数に等しくなります。
よって、n×nの場合の長方形の個数は
| n+1C2×n+1C2= | ( | n(n+1) 2 | ) | 2 |
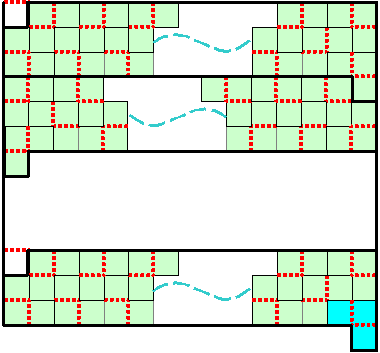
5×5の場合 18本
ー ー ー ー ー | | | ー ー ー | | | | | ー ー ー | | | | | ー ー ー | | | | | ー ー | | | ー ー ー ー ー6×6の場合 25本
ー ー ー ー ー ー | | | ー ー ー | | | | | | ー ー ー ー | | | | | ー ー ー ー | | | | | ー ー ー ー | | | | | | ー ー ー | | | | ー ー ー ー ー ー7×7の場合 34本
ー ー ー ー ー ー ー | | | | ー ー ー ー | | | | | | ー ー ー ー ー | | | | | | ー ー ー ー | | | | | | ー ー ー ー ー | | | | | | ー ー ー ー | | | | | | | ー ー ー | | | | ー ー ー ー ー ー ー8×8の場合 43本
ー ー ー ー ー ー ー ー | | | | | ー ー ー ー | | | | | | | ー ー ー ー ー ー | | | | | | | ー ー ー ー | | | | | | ー ー ー ー ー ー ー | | | | | | ー ー ー ー | | | | | | | ー ー ー ー ー ー | | | | | | | ー ー ー ー | | | | | ー ー ー ー ー ー ー ー【おまけ4】
まず、n×nの場合に、長方形をなくするために取り去らなければならないマッチ棒の最低本数の下限値を求めます。
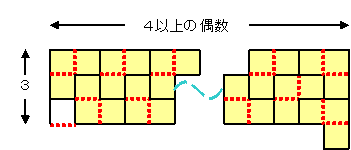
・nが偶数のとき
| 『 の多角形の数は最大で[ | n2 3 | ]。 |
この時、全体図形の内部で取り去らなければならないマッチ棒の数は
| [ | n2 3 | ]×2。 |
| [ | n2 3 | ]×2+1 となります。 |
| また | n2 3 | の剰余は1または0です。 |
これが最外周に付いていれば、1本のマッチ棒を取り去ることにより、単位正方形と最外周の正方形を同時になくすことができます。
| 従って、下限値は [ | n2 3 | ]×2+1 となります。 |
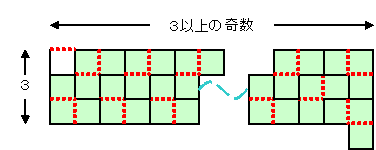
・nが奇数のとき
| 『 の多角形の数は最大で [ | n2 3 | ]。 |
ところが最外周の辺の単位正方形の数が奇数のため、各辺で『 を置く場所を偶数にするため、孤立正方形が少なくとも2個(全体図形の対角のコーナーに1個ずつ)必要です。
| n2 3 | が割り切れるとき、すなわちnが3の倍数のとき、 |
| 下限値は [ | n2 3 | ]×2+1となります。 |
| n2 3 | が割り切れないとき、すなわちnが3の倍数でないとき、 |
| 下限値は [ | n2 3 | ]×2+2となります。 |
下限値は以上のとおりですが、次に数学的帰納法を使って、一般のnに対し、下限値のマッチ棒を取り去って、求める配置が得られることを示します。
・nが偶数のとき
【問題2】および【おまけ3】で求めた配置を基本として、
(n+6)×(n+6)がまた下限値により実現できることを示すことで、
すべてのn≧4の偶数で実現できることを示します。
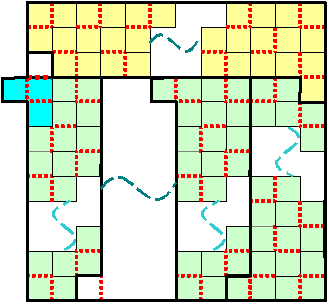
まず、6×6は【おまけ3】で求めたように12個の『 で完全に埋めることができます。
『 を下図で表すと、6×6を『 で埋めた図形は<図1>のようになります。
(若干紛らわしい図ですが角から追っていくと『 を切り出せます。)
『 の表現図形
・ー |<図1>
・ー・ーー・ |||・ー| |・ー|ー・ ・ー|ー・| |ー・||| ・ーー・ー・次にnをn≧4の偶数として6×nの図形は<図2>のように『 で完全に埋めることができます。
・ーー・ |・ー| ||ー・ ・ー|| |ー・| ・ーー・6×8
・ー・ー・ーー・ |||||・ー| |・ー・ー|ー・ ・ー|ー・ー・| |ー・||||| ・ーー・ー・ー・以下同一パターンの繰り返しで6×nを構成できます。
・ー・ー・ー ー・ ||||| ・ー| |・ー・ー |ー・ ・ー|ー・ ー・| |ー・||| || ・ーー・ー・ ー・次に、上の6×nの図形2個と6×6の図形1個で、<図3>の図形を作ります。
<図3>
ーーーーーー ーーーーーーーーーー |・・・・・・||・・・ ・・・・| |・・・・・・||・・・ ・・・・| n×6 n×n |・・・・・・||・・・ ・・・・| |・・・・・・||・・・ ・・・・| ーーーーーー ーーーーーーーーーー ーーーーーー ーーーーーーーーーー |・・・・・・||・・・ ・・・・| |・・・・・・||・・・ ・・・・| |・・・・・・||・・・ ・・・・| |・6×6・・||・・・6×n・・・・| |・・・・・・||・・・ ・・・・| |・・・・・・||・・・ ・・・・| ーーーーーー ーーーーーーーーーー以上で(n+6)×(n+6)の配置ができますが、最後に4つのブロックを結合(4つの長方形を1つにする)します。
<図4>
|| ー・・ー ー・・ー || ー ー | | | ー ー | | | ー ー ー ー | | | ー | ー | | | ー ー<図4>の部分を<図5>のようにすれば結合ができます。
<図5>
・ー ||ー・ ・ー|| ー・ ー ー | | ー ー ー | | | | ー ー | | | | ー ー ー | | ー ー以上で(n+6)×(n+6)の単一の配置ができました。
最後に、(もしあれば)右上角の仲間外れの正方形の最外周のマッチ棒を除くことにより、
(n+6)×(n+6)の長方形のない配置が実現し、孤立正方形があれば、右上角に配置されたままです。
| この時、取り除いたマッチ棒の数は[ | (n+6)2 3 | ]×2+1 です。 |
| [ | n2 3 | ]×2+1本のマッチ棒を取り除くことにより、 |
| なおn=2でも、取り除くマッチ棒の数は[ | n2 3 | ]×2+1となっています。 |
・nが奇数のとき
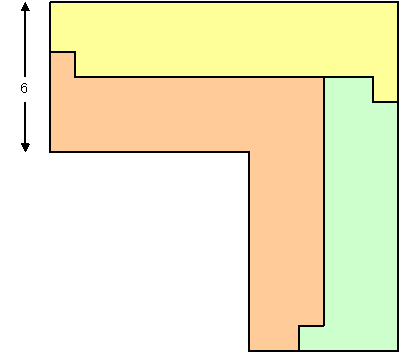
n≧2の偶数の場合のn×nを基本として、(n+3)×(n+3)の配置を考えます。
このために<図6>の配置を用意します。
ここで辺の数はn+3です。
また、×は孤立正方形を表します。
<図6>
・ー× |ー・ ・ー| |ー・ ・ー| | ー・ ・ー||ー・ー・ ー・ー・ー・× ||ー・|||| ||||||| ×・ーー・ー・ ー・ー・ー・ー・この配置のスペース部分にn×n(n≧2の偶数)の上で実現した図形を配置します。
nが3の倍数のときはn×nの図形に孤立正方形はなく、
<図6>の×の3つの孤立正方形をなくしても、
| 取り去るマッチ棒の数は[ | (n+3)2 3 | ]×2+1 で済みます。 |
| 結局、取り去るマッチ棒の数は[ | (n+3)2 3 | ]×2+2となります。 |
以上により、下限値のマッチ棒を取り去ることで、求める配置が実現できることが示されました。
またn=3のときも
| [ | n2 3 | ]×2+1本のマッチ棒を取り去れば長方形をなくすることができました。 |
| n≧2が偶数または3の倍数のとき、[ | n2 3 | ]×2+1 |
| それ以外のとき、[ | n2 3 | ]×2+2 |
いろいろなnの配置をいじり回してようやく証明に至りました。
この証明は実証的な泥臭い方法で、もう少し単純明快なやり方があるような気がするのですが・・・。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
初期長方形 個 取り除いたマッチ棒 本
現在の形
【問題2】
初期長方形 個 取り除いたマッチ棒 本
現在の形
【おまけ1、2】
(n+1C2)2
∵ 長方形は平行な2辺の2組で囲まれており、選ぶべき平行線は各組n+1本あるから。
【おまけ3】
(1)5×5
初期長方形 個 取り除いたマッチ棒 本
現在の形
(2)6×6
初期長方形 個 取り除いたマッチ棒 本
現在の形
(3)7×7
初期長方形 個 取り除いたマッチ棒 本
現在の形
(4)2×2
初期長方形 個 取り除いたマッチ棒 本
現在の形
【おまけ4】
| (1)nが偶数のとき n | 2 | −[ | n2−1 3 | ] |
| (2)nが奇数のとき n | 2 | −[ | n2−2 3 | ] |
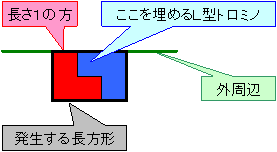
∵ 【必要性】
(1)全般およびnが偶数のとき
一番大きなn×nの正方形を消去するために外周の少なくとも1本をとる必要があります。
このとき1×1の正方形が1個消去され、1×1は残りn2−1個となります。
これらを効率的に消去するために、内部の1本をとると1×1の正方形が2個減りますが、これらで構成された1×2の長方形は残っています。
そこでもう一本、長さ2の側の一本をとる必要があります。
これの手順により、全部でL型トロミノ状につながった3個の1×1の正方形が消去されます。
つまり1×1の正方形3個につき、少なくとも2本の内部マッチをとらなければなりません。
| L型トロミノの数は最大 T=[ | n2−1 3 | ] です。 |
| 従って、L型トロミノの数は最大 T’=[ | n2−2 3 | ] です。 |

◆ 問題へもどる
◆ 今週の問題へ