『今週の問題』第215回　解答

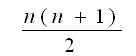
◆東京都　明 さんからの解答

【問題１−１】

手数：１５手
手順：下記２通り

1,2→移動先，3,4→移動先，5→移動先，5,3→最　初，4,1→最　初，
2→最　初，2,4→移動先，1,5→移動先，3→移動先，3,1→最　初，
5,2→最　初，4→最　初，4,5→移動先，2,3→移動先，1→移動先，

1→移動先，2,3→移動先，4,5→移動先，4→最　初，5,2→最　初，
3,1→最　初，3→移動先，1,5→移動先，2,4→移動先，2→最　初，
4,1→最　初，5,3→最　初，5→移動先，3,4→移動先，1,2→移動先，

手数：１６手
手順：下記

1,2→移動先，3,4→移動先，5→移動先，5,3→最　初，4,1→最　初，
2→最　初，2,4→移動先，1,5→移動先，3→移動先，3,1→最　初，
5,2→最　初，5→移動先，2,3→移動先，2→最　初，3→最　初，
5,4→最　初，

手数：２８手
手順：下記２通り

1,2→移動先，3,4→移動先，5,6→移動先，7→移動先，7,5→最　初，
6,3→最　初，4,1→最　初，2→最　初，2,4→移動先，1,6→移動先，
3,7→移動先，5→移動先，5,3→最　初，7,1→最　初，6,2→最　初，
4→最　初，4,6→移動先，2,7→移動先，1,5→移動先，3→移動先，
3,1→最　初，5,2→最　初，7,4→最　初，6→最　初，6,7→移動先，
4,5→移動先，2,3→移動先，1→移動先，

1→移動先，2,3→移動先，4,5→移動先，6,7→移動先，6→最　初，
7,4→最　初，5,2→最　初，3,1→最　初，3→移動先，1,5→移動先，
2,7→移動先，4,6→移動先，4→最　初，6,2→最　初，7,1→最　初，
5,3→最　初，5→移動先，3,7→移動先，1,6→移動先，2,4→移動先，
2→最　初，4,1→最　初，6,3→最　初，7,5→最　初，7→移動先，
5,6→移動先，3,4→移動先，1,2→移動先，

手数：３１手
手順：下記

1,2→移動先，3,4→移動先，5,6→移動先，7→移動先，7,5→最　初，
6,3→最　初，4,1→最　初，2→最　初，2,4→移動先，1,6→移動先，
3,7→移動先，5→移動先，5,3→最　初，7,1→最　初，6,2→最　初，
4→最　初，4,6→移動先，2,7→移動先，1,5→移動先，3→移動先，
3,1→最　初，5,2→最　初，7,4→最　初，7→移動先，4,5→移動先，
2,3→移動先，2→最　初，3→最　初，4→最　初，5→最　初，
7,6→最　初，

「移動先」の列に１〜ｎの順に並べるための最少手数
　n=2k+1のとき、(2k+1)(k+1)

理由

まず、最初の列と移動先の列を１つのつながった列と考えます。
最初の列と移動先の列の間でカードを１枚ずつ移動した場合は、つながった列の中ではカードの順番は替わる事がありません。
２枚のカードを移動した場合は、つながった列の中では２枚の間で順番が置換されることになります。
隣合ったカードの置換ができれば、適当に置換を繰り返すことでカードの並びを任意にすることができます。

【問題１】【問題２】の答えのように２枚ずつカードを列間移動させ、最後に残った１枚を移動させるk+1回の移動を繰り返すことを考えます。

１セット（k+1回、2k+1枚）の移動でのカードの順番は次のようになります。

1,2,3,4・・・,2k-2,2k-1,2k,2k+1　→　2,1,4.3,・・・,2k-3,2k,2k-1,2k+1

2,4,1,6・・・,2k,2k-3,2k+1,2k-1

2k+1,2k,2k-1,2k-2・・・,4,3,2,1

次に最小手数について考えます。

最初の列から移動先の列へカードの山を題意に添って移動させると、つながった列としてみれば、始めと最終形の間で、列のカードの順番の転倒（２枚のカード間の数の順番の逆転）の数は、
(2k+1)k　個になります。
したがって２つの列の間で２枚組の移動を最低　(2k+1)k回しなければなりません。

ところで、２つの列の間で２枚組の移動をする場合、移動の方向を変えるとき、少なくとも１枚のカードの移動をしなければなりません。
（さもないと次の２枚組の移動は１つ前の状態に戻すだけで無駄な手となります。）

(2k+1)k回の２枚のカードを移動させるとき、列間の1方向への移動は最大　k回しかできないため、
移動の方向の変化は最低 (2k+1)-1=2k 回必要です。

以上により、(2k+1)k組のカードの転倒には (2k+1)k+k回のカード移動が必要です。

ただし２枚ずつのカード移動をしたとき、最後に１枚のカードが最初の列に残るため、すべてのカードを移動先へ移すためには
最低でも (2k+1)k+k+1=(2k+1)(k+1)回のカード移動が必要になります。

以上により、２枚ずつカードを列間移動させ、最後に残った１枚を移動させるk+1回の移動を繰り返すことで、最小手数のカード移動ができることが証明されました。

最初に１枚を移動し、次に２枚ずつ k回移動させる方法でも同様です。
最小手数で指定の並びを実現する方法はこの２通りしかないことも明らかです。

【おまけ２】

指定された並びにするため、【問題１】【問題２】と同様な方法でカード移動をすれば
k(2k+5)-2 回で可能なことは判りますが、これが最小手数かはわかりません。
（k が２以上のときは少なくとも 2k+1 回の移動方向の変更が必要なため、
(2k+1)(k+1) 回が下限であることは判ります。）

n=3,5,7については計算機でk(2k+5)-2 回が最小手数であることを確かめました。
(n=9 以上ではメモリ不足で計算できませんでした。）

ちなみに　n=5での最小手数の移動方法は２２通り。
n=7での最小手数の移動方法は５３０通りありました。

参考で、コメントなしですが手数、手順を求めるためのプログラムを添付します。
（10進ＢＡＳＩＣです。）

◆滋賀県　松尾　さんからの解答

【問題１−１】

１５手です。手順は以下のとおりです。

1→移動先，2,3→移動先，4,5→移動先，4→最　初，5,2→最　初，
3,1→最　初，3→移動先，1,5→移動先，2,4→移動先，2→最　初，
4,1→最　初，5,3→最　初，5→移動先，3,4→移動先，1,2→移動先

【問題１−２】

「最小手数です。」との表示が出ないので自信がありませんが、１６手です。
手順は以下のとおりです。

1,2→移動先，3,4→移動先，5→移動先，5,3→最　初，4,1→最　初，
2→最　初，2,4→移動先，1,5→移動先，3→移動先，3,1→最　初，
5,2→最　初，5→移動先，2,3→移動先，2→最　初，3→最　初，5,4→最　初

２８手です。手順は以下のとおりです。

1→移動先，2,3→移動先，4,5→移動先，6,7→移動先，6→最　初，
7,4→最　初，5,2→最　初，3,1→最　初，3→移動先，1,5→移動先，
2,7→移動先，4,6→移動先，4→最　初，6,2→最　初，7,1→最　初，
5,3→最　初，5→移動先，3,7→移動先，1,6→移動先，2,4→移動先，
2→最　初，4,1→最　初，6,3→最　初，7,5→最　初，7→移動先，
5,6→移動先，3,4→移動先，1,2→移動先

「最小手数です。」との表示が出ないので自信がありませんが、３１手です。
手順は以下のとおりです。

1,2→移動先，3,4→移動先，5,6→移動先，7→移動先，7,5→最　初，
6,3→最　初，4,1→最　初，2→最　初，2,4→移動先，1,6→移動先，
3,7→移動先，5→移動先，5,3→最　初，7,1→最　初，6,2→最　初，
4→最　初，4,6→移動先，2,7→移動先，1,5→移動先，3→移動先，
3,1→最　初，5,2→最　初，7,4→最　初，7→移動先，4,5→移動先，
2,3→移動先，2→最　初，3→最　初，4→最　初，5→最　初，
7,6→最　初

何度かやっていくうちに最初のカードを１枚動かし、次から２枚づつ動かすという方法に出会いました。
この方法では　n＝５のとき、以下のように変化します。
「最初」を「左」、「移動先」を「右」で表します。括弧内は手数です。

（０）　　（３）　　（６）　　（９）　（１２）　（１５）
左　右　　左　右　　左　右　　左　右　　左　右　　左　右　　
１　　　　　　４　　３　　　　　　２　　５　　　　　　１
２　　　　　　５　　１　　　　　　４　　３　　　　　　２
３　　　　　　２　　５　　　　　　１　　４　　　　　　３
４　　　　　　３　　２　　　　　　５　　１　　　　　　４
５　　　　　　１　　４　　　　　　３　　２　　　　　　５

このためにカードは２つの列を移動するのですが、隣の列に移動する場合、５枚のカードすべてを移動しないと完成直前の状態になりません。
例えば５のカードを残したまま５を上に移動することはできません。
すべてのカードを隣の列に移動する手数は最小で３手、
カードがn枚の時は（n＋１）÷２（手）です。

何回列を移動しなくてはならないかですが、左の列にカードがある時の１と５の位置に注目します。
５は２つづつ上に、１は最初は１つで、次は２つ下がります。
ほかの方法を試みましたが、１と５の上下移動は２つまでで３つ以上上下することはありません。

完成直前、１２手目の状態になるには１は３つ下がり、５は４つ上がります。
このためn＝５の場合、
「最初」ー＞「移動先」ー＞「最初」ー＞「移動先」ー ＞「最初」　で４回、
カードがn枚の場合は、移動は（n−１）回必要です。

最後に５つのカードを右の列に移動して完成ですから、移動は５回、n枚の時はn回です。
以上から最短の手数は　　n（ｎ＋１）÷２（手）　　です。

なお、カードの動かし方で、上から１枚、次から２枚を動かしましたが、上から２枚づつ動かし、最後の１枚を動かす方法でも同じ手数でできます。

【おまけ２】

n＝５のとき、最初から２枚づつ、残りの１枚を一番上に移動するという方法で途中まで動かします。
４が「移動先」の下に来たら、４を残して残りを移動します。
１が「最初」の下に来たら、１のみ残して残りを移動します。
この後、移動は１枚、２枚と動かします。 最後に１枚、１枚、２枚と動かし完成です。

この方法では以下のように変化します。
「最初」を「左」、「移動先」を「右」で表します。
括弧内は手数です。

n＝５の場合の変化

（０）　　（３）　　（６）　　（９）　（１１）　（１３）　（１６）
左　右　　左　右　　左　右　　左　右　　左　右　　左　右　　左　右
１　　　　　　５　　２　　　　　　３　　　　　　　　　　　　５
２　　　　　　３　　４　　　　　　１　　５　　　　　　２　　４
３　　　　　　４　　１　　　　　　５　　２　　　　　　３　　３
４　　　　　　１　　５　　　　　　２　　３　　　　　　５　　２
５　　　　　　２　　３　　　　　　４　　１　４　　１　４　　１

何回列を移動しなくてはならないかは【おまけ１】と同じで４回、カードがn枚の場合は、（n−１）回です。
これで「最初」の列に並びますが、これではできません。
５の位置は上から２枚目となり、また、２、３、４のカードの位置が合わないからです。
結局、もう１往復する必要があります。

ただ、途中で４が「移動先」の下１枚目に来るので、移動の手数は１手減ります。
上図の９手目です。
また、１も途中で「最初」の下１枚目にくるので、手数 は１手減ります。
上図の１１手目です。
合計で２手減ります。

完成直前の「移動先」の列に並ぶまでにかかった手数は【おまけ１】の手数から２手減らした数の１３手、
カードがn枚の時は　n（ｎ＋１）÷２−２（手） です。

そして最後に４つのカードを右の列に移動して完成ですが、上から１枚、１枚、２枚と移動するので、手数は３手、
n枚の時はn−２手です。

結局、手数は
　n（ｎ＋１）÷２−２　＋　n−２（手）
＝n（ｎ＋１）÷２　＋　n−４（手）です。

n＝７の場合の変化です。

（０）　　（４）　　（８）　（１２）　（１６）　（２０）　（２３）
左　右　　左　右　　左　右　　左　右　　左　右　　左　右　　左　右
１　　　　　　７　　２　　　　　　５　　４　　　　　　３
２　　　　　　５　　４　　　　　　３　　６　　　　　　１　　７
３　　　　　　６　　１　　　　　　７　　２　　　　　　５　　４
４　　　　　　３　　６　　　　　　１　　７　　　　　　２　　５
５　　　　　　４　　３　　　　　　６　　１　　　　　　７　　２
６　　　　　　１　　７　　　　　　２　　５　　　　　　４　　３
７　　　　　　２　　５　　　　　　４　　３　　　　　　６　　１　６

　　（２６）　　（３１）
　　　左　右　　左　右
　　　　　　　　７
　　　　　２　　６
　　　　　３　　５
　　　　　４　　４
　　　　　５　　３
　　　　　７　　２
　　　１　６　　１

◆愛知県　Y.M.Ojisan　さんからの解答

【問題１−１】　１５手

1,2→移動先，3,4→移動先，5→移動先，5,3→最　初，4,1→最　初，
2→最　初，2,4→移動先，1,5→移動先，3→移動先，3,1→最　初，
5,2→最　初，4→最　初，4,5→移動先，2,3→移動先，1→移動先，

1,2→移動先，3,4→移動先，5→移動先，5,3→最　初，4,1→最　初，
2→最　初，2,4→移動先，1,5→移動先，3→移動先，3,1→最　初，
5,2→最　初，5→移動先，2,3→移動先，2→最　初，3→最　初，
5,4→最　初，

1,2→移動先，3,4→移動先，5,6→移動先，7→移動先，7,5→最　初，
6,3→最　初，4,1→最　初，2→最　初，2,4→移動先，1,6→移動先，
3,7→移動先，5→移動先，5,3→最　初，7,1→最　初，6,2→最　初，
4→最　初，4,6→移動先，2,7→移動先，1,5→移動先，3→移動先，
3,1→最　初，5,2→最　初，7,4→最　初，6→最　初，6,7→移動先，
4,5→移動先，2,3→移動先，1→移動先，

1,2→移動先，3,4→移動先，5,6→移動先，7→移動先，7,5→最　初，
6,3→最　初，4,1→最　初，2→最　初，2,4→移動先，1,6→移動先，
3,7→移動先，5→移動先，5,3→最　初，7,1→最　初，6,2→最　初，
4→最　初，4,6→移動先，2,7→移動先，1,5→移動先，3→移動先，
3,1→最　初，5,2→最　初，7,4→最　初，7→移動先，4,5→移動先，
2,3→移動先，2→最　初，3→最　初，4→最　初，5→最　初，
7,6→最　初，

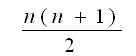
【おまけ２】 　(予想)

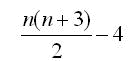
【証明】
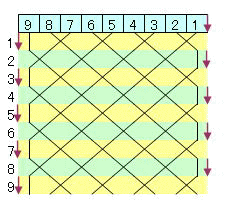
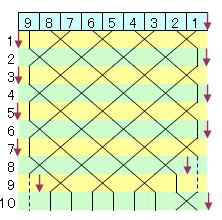
　下図（ｎ＝９の場合）のようにカードのある部分だけ上部を付き合わせると、９個のセルにカードがならび、
ｎ＋１個の位置の何れかの位置に境界が一つあるという図になる。
　この場合、１個だけ移動するのは、境界が１個ずれるだけと同じである。また、２個の移動は、境界が２個ずれることと、通過した２セルのカード交換が行われることと同じである。

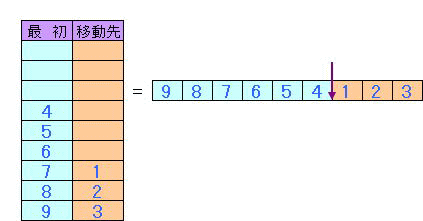
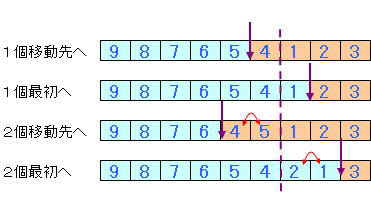
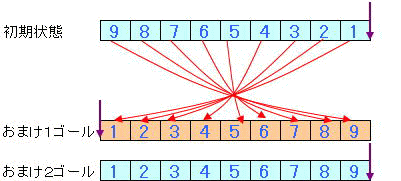
　以上の表示方法で初期状態とゴール状態を表すと下図である。
いずれのゴールもカード配置にのみ注目すると逆順である。境界位置が異なっているだけである。　
　一方、上図に示すように１個移動ではカードの並びは変化せず、２個の場合は互換一回に対応している。

【十分条件】
【おまけ１】

下図のように２個２個。。。最後１個移動を左右にｎ回スイープすればカード順は逆転し、かつ矢印は左端に来る。
このときの手順数は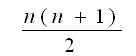である。

【おまけ２】

下図のように２個２個。。。最後１個移動を左右にｎ−２回スイープし、ｎ−１回目は最後の１個移動の前でスイープを止める。
次に逆スイープを行うが最初に１個移動し、２個２個。。。２個移動をできるところまで行う。
最後のスイープでは１個１個。。。。。１個移動を行い最後に２個移動を行う。
以上でカード順は逆転し、矢印は右端にくる。
このときの手順数は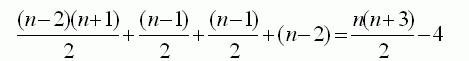である。
（青破線はそのままを表す）
これは単順に、おまけ１の手順の最後を除く手順の後、１個移動のみで右へ戻る方法よりは２回少ない。
　　

【必要条件】

Ｎ枚のカードを逆順に並び替えるには　互換は全部で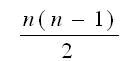回必要である。
これを「必要互換数」とよぶ。
即ち、どんなに少なくても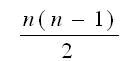回の手数は必須である。
ただし、２個移動ばかりでは矢印の位置が２づつ左右するだけなので、ｎ＝９の場合なら４回より後は戻るしかなく、かつそれは前回と同じ互換なので無駄である。
一般には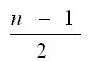回連続が最高である。
これを「最高連続互換回数」とよぶ。

　従って、状況を変えるには　ここに「１個移動」を挟む必要がある。
必要互換数／最高連続互換回数＝ｎであるので　少なくともｎ−１回の「１個移動」が余分に必要である。
ｎは奇数であるので、区分境界（↓）はほぼ左の端に行っている。
完全に左端にゴールするには、後１回「１個移動」が必要である。
　よって、【おまけ１、２】の手数は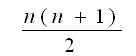回より小さくない。

　【おまけ２】の場合は、PCで虱潰しに探索したところ　ｎ＝５，７，９の場合は十分条件で示した手数が最小であることが確認された。
多分、それ以上のときも十分条件で示した手数が最小と思われるが証明できなかった。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる