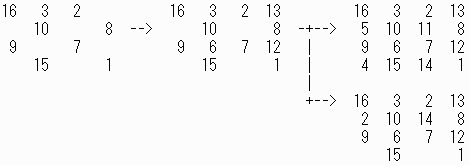
◆神奈川県 アンパンマン さんからの解答
【問題1】
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
【問題2】
4×4の魔方陣の各マスの値の行列をAに定義します。
(A=[aij])
a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44
すると、
a12+a13+a42+a43=34
a12+a24+a43+a31=34
a12+a21+a43+a34=34
a22+a23+a32+a33=34
a11+a14+a41+a44=34
a11+a32+a23+a44=34
などです。
各値(aij)が合計(=34)に使われる回数(bij)の行列B=[bij]を以下に示す。
5 6 6 5 6 5 5 6 6 5 5 6 5 6 6 51回の合計に4つの数字を使うため、
【問題3】
各数字をノードにして、合計が34になる数字を線でリンクして、グラフで表示してわかるように、対称的に入れ替わっても性質が変わらないので、入れ替わる方法が次のようにあります。
a)縦1と2の入れ替え、縦3と4の入れ替え、=1通り
b)横1と2の入れ替え、横3と4の入れ替え、=1通り
c) a)とb)の組み合わせ =1通り
d)元もパターン=1通り、よってa)からd)は4通り
d)その他(1から4を逆順と5から8を逆順にするなど)計4C2/2=3通り
e)真ん中の縦2列の中の1と2列の入れ替え、3と4列の入れ替え、計2通り
よって、 4*4C2/2*2=24通り
【おまけ】
n次元まで拡張可能ですが、とりあえず3次元の「magic cube」です。
レイヤ1 1 56 57 16 48 25 24 33 29 44 37 20 52 5 12 61 レイヤ2 62 11 6 51 19 38 43 30 34 23 26 47 15 58 55 2 レイヤ3 63 10 7 50 18 39 42 31 35 22 27 46 14 59 54 3 レイヤ4 4 53 60 13 45 28 21 36 32 41 40 17 49 8 9 64縦、横、斜めなどの線上の四つの数字の合計も130になります。
◆大阪府 二神 孝明 さんからの解答
【おまけ】
1〜25の数字を一個ずつ。使われてる数字は不可。
| 11 | □ | 15 | □ | 25 |
| □ | □ | □ | □ | □ |
| 21 | □ | 18 | □ | 10 |
| □ | □ | □ | □ | □ |
| 13 | □ | 2 | □ | 9 |
◆広島県 清川 育男 さんからの解答
【問題1】
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
| 16 | 5 | 2 | 11 |
| 3 | 10 | 13 | 8 |
| 9 | 4 | 7 | 14 |
| 6 | 15 | 12 | 1 |
【問題2】
| 16 | 13 | ||
| 10 | 11 | ||
| 6 | 7 | ||
| 4 | 1 |
| 16 | 11 | ||
| 10 | 13 | ||
| 4 | 7 | ||
| 6 | 1 |
入れ子型になっている。
【問題3】
和は、 ((1+16)*16/2)/4=34
したがって、左上隅は16。
| 16 | a | 2 | 16-a |
| b | 10 | 16-b | 8 |
| 9 | 9-a | 7 | 9+a |
| 9-b | 15 | 9+b | 1 |
a+b=8
(a=3,b=5),(a=5,b=3)
2通り。
◆茨城県 長すぎる名前 さんからの解答
【問題3】
各行・列の数の和は34
見えている数字の和と残りの数は、
| A | B | C | D | 和 | 残 | |
| 1 | □ | □ | 2 | □ | 2 | 32 |
| 2 | □ | 10 | □ | 8 | 18 | 16 |
| 3 | 9 | □ | 7 | □ | 16 | 18 |
| 4 | □ | 15 | □ | 1 | 16 | 18 |
| 和 | 9 | 25 | 9 | 9 | ||
| 残 | 25 | 9 | 25 | 25 |
18=16+2、25=16+9で2も9も既に使われているので、16が入るマスは、A1の位置しかない。
| A | B | C | D | 和 | 残 | |
| 1 | 16 | □ | 2 | □ | 18 | 16 |
| 2 | □ | 10 | □ | 8 | 18 | 16 |
| 3 | 9 | □ | 7 | □ | 16 | 18 |
| 4 | □ | 15 | □ | 1 | 16 | 18 |
| 和 | 25 | 25 | 9 | 9 | ||
| 残 | 9 | 9 | 25 | 25 |
A列とC列、B列とD列の空きマスに着目すると、2行2列の方陣2つに分割できる。
2つの方陣の各行・列の数の和は同じ構造になる。
方陣AC
| A | C | 空きマスの数の和 | |
| 2 | □ | □ | 16 |
| 4 | □ | □ | 18 |
| 和 | 9 | 25 |
方陣BD
| B | D | 空きマスの数の和 | |
| 1 | □ | □ | 16 |
| 3 | □ | □ | 18 |
| 和 | 9 | 25 |
まず方陣ACについて考える。
使われていない数は
3,4,5,6,11,12,13,14
足して9になる組合せ (3,6) (4,5) (5,4) (6,3)
足して25になる組合せ (11,14) (12,13) (13,12) (14,11)
足して16になる組合せ (3,13) (4,12) (5,11)
足して18になる組合せ (4,14) (5,13) (6,12)
A2を決めるとA4、C2が決まり、D4も決まる。
(A2,A4,C2,C4)
=(3,6,13,12)…(1)
=(4,5,12,13)…(2)
=(5,4,11,14)…(3)
この3通りに対応する方陣BDのマスの埋め方(B1,B3,D1,D3)は、
(1)… (5,4,11,14)
(2)… なし
(3)… (3,6,13,12)
よって2通り。
【問題2】
◆静岡県 つぼちゃん さんからの解答
【問題1】
1〜16までの数字を足すと136。
横は4通りあるから136÷4=34 で、1列の和は34になる。
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
| 16 | 5 | 2 | 11 |
| 3 | 10 | 13 | 8 |
| 9 | 4 | 7 | 14 |
| 6 | 15 | 12 | 1 |
【問題2】
16マスを十字に切って、左上、右上、左下、右下の4つのブロックに分けると、その1つのブロックの4つの数の和も同じになる。
【問題3】
2通り
まず、右下のブロックに注目して、4つの数の和が34になるには、残り2つの数字の和が26にならなければならない。
残っている数でこのような数の組み合わせは12と14しかない。
同様に、右上のブロックの4つの数の和が34になるには、残り2つの数字の和が24にならなければならない。
残っている数でこのような数の組み合わせは11と13しかない。
同様に、左下のブロックの4つの数の和が34になるには、残り2つの数字の和が10にならなければならない。
残っている数でこのような数の組み合わせは4と6しかない。
残った数字は、3,5,16で、3数の和は24で、これらは左上のブロックに入る数字となる。
ここで、右下のブロックに12と14を固定すると、その他に入る数字は1通りしかない。
12と14を入れ替えてもその他に入る数字は1通りしかない。
よって、合計2通り。
◆滋賀県 松尾 さんからの解答
【問題1】【問題3】
縦、横、斜めの合計は 1から16までの合計の4分の1、34になります。
1行目の1列目には16が入ります。
1列目には 16、9があり、残りの2つの数の合計は9です。
2列目には 10、15があり、残りの2つの数の合計は9です。
2つの数の合計が9になるのは 残った3,4,5,6,11,12,13,14のうち 4、5 または 3、6 の2とおりです。
同様に、3列目、4列目の合計は9、残りの数の合計は25。
2つの数の合計が25になるのは 残った3,4,5,6,11,12,13,14のうち 11、14 または 12、13 の2とおりです。
以下、数をいれてみます。
まず、1行目、2列目に 3 を入れてみます。(下図左)
3行目、2列目は6です。
縦、横が34になるように数を入れると、下図中までは決まります。
4列目は 12、13 の組が入ったので、3列目には 11、14 が入ります。
2行目、3列目に11を入れてみるとできました。(下図右上)
2行目、3列目に14を入れてみると、残りを入れていくうちに2が二つ出て、できません。(下図右下)
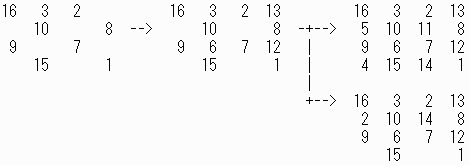
1行目2列目に 6をいれます。 10が二つ出て、できません。(下図)
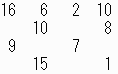
1行目、2列目に 4 を入れてみます。(下図左)
3行目、2列目は 5 です。
縦、横が34になるように数を入れると、下図中までは決まります。
4列目は 12、13 の組が入ったので、3列目には 11、14 が入ります。
2行目、3列目に11を入れてみると、残りを入れていくうちに4が二つ出て、できません。(下図右下)
2行目、3列目に14を入れてみると、残りを入れていくうちに7が二つ出て、できません。(下図右下)
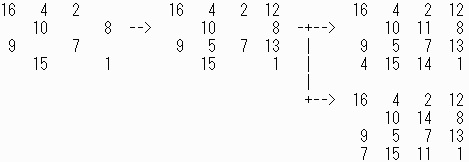
1行目、2列目に 5 を入れてみます。(下図左)
3行目、2列目は 4 です。
縦、横が34になるように数を入れると、下図中までは決まります。
4列目は 11、14 の組が入ったので、3列目には 12、13 が入ります。
2行目、3列目に12を入れてみると、残りを入れていくうちに5が二つ出て、できません。(下図右上)
2行目、3列目に13を入れてみるとできました。(下図右下)
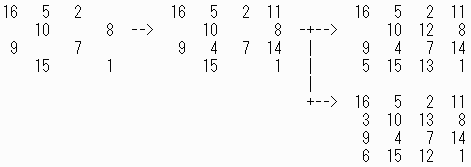
結局、以下の二通りです。
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
| 16 | 5 | 2 | 11 |
| 3 | 10 | 13 | 8 |
| 9 | 4 | 7 | 14 |
| 6 | 15 | 12 | 1 |
【問題2】
1列目と4列目、あるいは2列目と3列目を入れ替えても魔法陣として成立します。
また、1行目と4行目、あるいは2行目と3行目を入れ替えても魔法陣として成立します。
これを繰り返しても成立します。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1,3】
下図の2通りあります。
証明
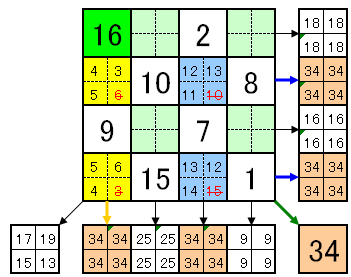
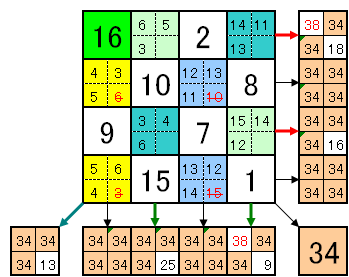
【問題2】
縦横斜め以外の特別な位置関係にある4箇所に関しても、多くのケースでその合計が同じ値:34である。
下図参照
【おまけ】
二十四節気の漢字の総画数の魔法陣(5×5)です。
総画数調整のため「二十四節気」で旧字「氣」を採用しています。
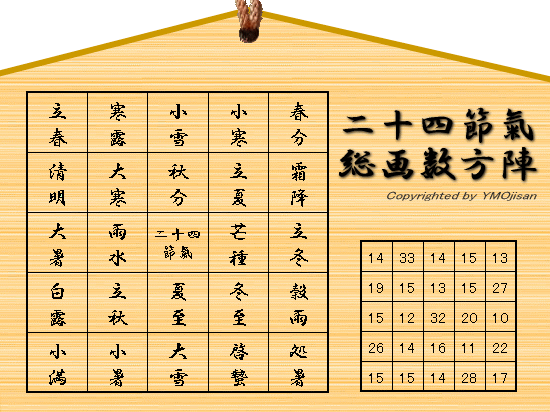
| 節 氣 | 小 寒 | 大 寒 | 立 春 | 雨 水 | 啓 蟄 | 春 分 | 清 明 | 穀 雨 | 立 夏 | 小 満 | 芒 種 | 夏 至 | 小 暑 | 大 暑 | 立 秋 | 処 暑 | 白 露 | 秋 分 | 寒 露 | 霜 降 | 立 冬 | 小 雪 | 大 雪 | 冬 至 |
| 読み | しょうかん | だいかん | りっしゅん | う す い | けいちつ | しゅんぶん | せいめい | こ く う | り っ か | しょうまん | ぼうしゅ | げ し | しょうしょ | たいしょ | りっしゅう | しょしょ | は く ろ | しゅうぶん | か ん ろ | そうこう | りっとう | しょうせつ | たいせつ | と う じ |
| 平成17年暦 | 1月5日 | 1月20日 | 2月4日 | 2月18日 | 3月5日 | 3月20日 | 4月5日 | 4月20日 | 5月5日 | 5月21日 | 6月5日 | 6月21日 | 7月7日 | 7月23日 | 8月7日 | 8月23日 | 9月7日 | 9月23日 | 10月8日 | 10月23日 | 11月7日 | 11月22日 | 12月7日 | 12月22日 |
| 総画数 | 15 | 15 | 14 | 12 | 28 | 13 | 19 | 22 | 15 | 15 | 20 | 16 | 15 | 15 | 14 | 17 | 26 | 13 | 33 | 27 | 10 | 14 | 14 | 11 |
◆ 問題へもどる
◆ 今週の問題へ