c(n)=A(
ちょっと答えがはっきりしないのですが、とりあえず寄せられた解答を掲載しておきます。
◆神奈川県 アンパンマン さんからの解答
【問題1】
24回
1→奇 数,2→空き1,3→空き2,1→空き2,4→奇 数, 2→奇 数,5→偶 数,6→空き1,5→最 初,2→偶 数, 4→空き1,2→空き1,5→偶 数,7→奇 数,5→奇 数, 8→偶 数,1→最 初,3→奇 数,1→奇 数,2→最 初, 4→空き2,6→偶 数,4→偶 数,2→偶 数,【問題2】
a(n)を1から2nまでの数字カードを並び替える最少回数とする。
Heapの高さを抑えることによって、動かす回数を最小限にすることがあできる。
そのため、最小回数の手順は
2から2n-2の偶数を空き1に、1から2n-5の奇数を空き2に、2n-3を偶数列に動かす→ d(n-1)回 2n-1を奇数列に動かす。 → 1回 2n-3を奇数列に動かす。 → 1回 1から2n-5の奇数を奇数列に動かす。 → b(n-2)回 2nを偶数列に動かす。 → 1回 2から2n-2の偶数を偶数列に動かす。 → c(n-1)回よって a(n)=d(n-1)+3+b(n-2)+c(n-1)
ここで、b(n)とは1からnまでのカードを別の列に動かす最小回数
(偶奇別なし、大きい数字は下にある、予備列1つ)とする(=Tower of Hanoi問題)。
b(n)=2b(n-1)+1, b(0)=0,b(1)=1 → b(n)=2n-1
c(n)とは1からnまでのカードを別の列に動かす最小回数
(偶奇別なし、大きい数字は下にある、予備列2つ)とする。
c(n)=2c(n-1)+3, c(0)=0,c(1)=1,c(2)=3 →
c(n)=A(![]() )n+B(-
)n+B(-![]() )n+C
)n+C
| c(0)、c(1),c(2)により、A= | 3+2 2 | 、B= | 3-2 2 | , C=-3 |
d(n-1)は(実際に入れる列が違うが、動かす手順として以下である。)
2から2n-4の偶数を空き1に、1から2n-7の奇数を空き2に、2n-5を偶数列に動かす→ d(n-2)回 1から2n-7の奇数を偶数列に動かす。 → c(n-3)回 2n-3を奇数列に動かす。 → 1回 2n-2を空き2に動かす → 1回 2n-3を2n-1の上に動かす(「最初」の列) → 1回 2から2n-4の偶数を空き2に動かす → b(n-2)回 2n-3を空き1に動かす → 1回よって、
d(n-1)=d(n-2)+c(n-3)+b(n-2)+4
=d(n-2)+A(![]() )n-3+B(-
)n-3+B(-![]() )n-3+2n-2, n>3
)n-3+2n-2, n>3
つまり
d(n)=d(n-1)+A(![]() )n-2+B(-
)n-2+B(-![]() )n-2+2n-1, n>2
)n-2+2n-1, n>2
d(2)=5により、
| d(n)=d(2)+ | A | - | B 1+ | +2n-4 |
| = | A | - | B 1+ | +2n+1 |
よって、
a(n)=d(n-1)+3+b(n-2)+c(n-1)
| = | A | - | B 1+ | +2n-1+1+3+2n-2-1+A( |
| = | A | - | B 1+ | +3*2n-2+A( |
| a(4)=3*4+ | 3+ | - | 3-2 | +(3+ |
【問題3】
A(n)=a(n)になる通り数 B(n)=b(n)になる通り数 C(n)=c(n)になる通り数 D(n)=d(n)になる通り数B(n)=1
C(n)は二つの列が入れ替えられるため、
C(n)=2C(n-2), C(0)=C(1)=1によりC(n)=2[n/2]
D(n)=4*C(n-3)*B(n-2)*D(n-1)=2[(n+1)/2]*D(n-1), n>2
D(2)=4により
D(n)=2[(n+1)/2]+...+3*D(2)=2[(n+1)/2]*[(n+3)/2]/2-1
A(n)=4*D(n-1)*B(n-2)*C(n-1)
=4*2[(n+1)/2]*[(n+3)/2]/2-1*2[(n-1)/2]
=4*2[(n+1)/2]*[(n+3)/2]/2-1*2[(n-1)/2]
=2[(n+1)/2]*[(n+7)/2]/2
A(4)=25=32
【おまけ】
28回
1→空き1,2→空き2,3→奇 数,4→偶 数,1→奇 数, 5→空き1,2→偶 数,6→空き2,1→最 初,3→空き1, 1→空き1,7→奇 数,6→最 初,1→奇 数,3→空き2, 1→空き2,5→奇 数,1→空き1,3→奇 数,1→奇 数, 2→空き1,6→空き2,4→空き2,8→偶 数,4→最 初, 6→偶 数,4→偶 数,2→偶 数,最小回数の手順は
2から2n-4の偶数を偶数列に、1から2n-5の奇数を奇数列に動かす→ e(n-2)回 2n-3を空き1列に動かす。 → 1回 2n-2を空き2列に動かす。 → 1回 2n-1を奇数列に動かす → 1回 1から2n-3の奇数を奇数列に動かす。 → b(n-1)回 2n-2を2nの上に動かす → 1回 2から2n-4の偶数を空き2列に動かす。 → c(n-2)回 2n-2を空き1に動かす → 1回 2nを偶数列に動かす → 1回 2から2n-2の偶数を偶数列に動かす。 → c(n-1)回a(n)=e(n-2)+b(n-1)+c(n-1)+c(n-2)+6
e(n-2)は(実際に入れる列が違うが、動かす手順として以下である。)
2から2n-6の偶数を空き1に、1から2n-5の奇数を空き2に動かす→ e(n-3)回 2n-5を奇数列に動かす。 → 1回 2n-4を偶数列に動かす。 → 1回 1から2n-7の奇数を奇数列に動かす。 → b(n-3)回 2から2n-6の偶数を偶数列に動かす。 → b(n-3)回よって、
e(n)=e(n-1)+2+2b(n-1)
=e(n-1)+2n
=e(0)+2n+1-1
=2n+1-1
| a(n)=2n-1-1+2n-1-1+A( |
| =2n+ | (7+5 2 | + | (7-5 2 | -2 |
a(4)=16+14-2=28
◆広島県 清川 育男 さんからの解答
【問題1】
24回
1→偶 数,2→空き1,3→奇 数,4→空き2,2→空き2, 5→空き1,3→空き1,1→空き1,6→偶 数,7→奇 数, 1→奇 数,6→最 初,3→偶 数,1→偶 数,5→奇 数, 1→空き1,3→奇 数,1→奇 数,6→空き1,8→偶 数, 2→最 初,6→偶 数,4→偶 数,2→偶 数,【問題2】
プログラムで確認しました。
【問題3】
必要条件と思われる枝狩りをして探索しました。
108通りでした。
初手による分類 1-1 12通り 1-3 72通り 1-4 12通り 1-5 12通り -----------------合計 108通り
出力例
全結果はこちらです。
24 手 NO. 1 1 - 2 1 - 4 1 - 3 1 - 5 4 - 5 1 - 4 3 - 4 2 - 4 1 - 2 1 - 3 2 - 1 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 1 5 - 2 1 - 2 NO. 2 1 - 2 1 - 4 1 - 3 1 - 5 4 - 5 1 - 4 3 - 4 2 - 4 1 - 2 1 - 3 2 - 1 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 4 5 - 2 4 - 2 NO. 3 1 - 2 1 - 4 1 - 3 1 - 5 4 - 5 1 - 4 3 - 4 2 - 4 1 - 2 1 - 3 2 - 1 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 5 - 1 4 - 2 5 - 2 1 - 2 NO. 4 1 - 2 1 - 4 1 - 3 1 - 5 4 - 5 1 - 4 3 - 4 2 - 4 1 - 2 1 - 3 4 - 3 2 - 1 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 1 5 - 2 1 - 2 NO. 5 1 - 2 1 - 4 1 - 3 1 - 5 4 - 5 1 - 4 3 - 4 2 - 4 1 - 2 1 - 3 4 - 3 2 - 1 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 4 5 - 2 4 - 2以下略(全結果参照)
最小回数14回で可能となる場合を、10回を選んだ後すなわち11回目を迎える局面での分類
1) (8)(6)(7)(531)(42) 18
2) (8)(6)(7)(42)(531) 18
3) (8)(531)(7)(6)(42) 36
4) (8)(531)(7)(42)(6) 36
-----
108 (通り) 【おまけ】「最初」の列を奇数列とすると、
1 3 2 5 4 □ 8 7 6 □ -------------------- 1 2 3 4 5となり不可能。
●(1-10)の場合
44 手 2592 通り?
NO. 1 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 1 - 4 3 - 2 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 1 5 - 4 5 - 2 4 - 2 1 - 2 NO. 2 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 1 - 4 3 - 2 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 4 5 - 1 5 - 2 1 - 2 4 - 2 NO. 3 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 1 - 4 3 - 2 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 5 - 1 4 - 2 5 - 4 5 - 2 4 - 2 1 - 2 NO. 4 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 3 - 2 1 - 4 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 1 5 - 4 5 - 2 4 - 2 1 - 2 NO. 5 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 3 - 2 1 - 4 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 4 - 2 5 - 4 5 - 1 5 - 2 1 - 2 4 - 2 NO. 6 1 - 2 1 - 3 1 - 4 2 - 4 1 - 2 3 - 2 1 - 3 1 - 5 3 - 1 2 - 3 2 - 5 3 - 5 1 - 3 1 - 2 3 - 2 4 - 3 4 - 2 3 - 2 1 - 4 1 - 3 4 - 1 2 - 4 2 - 3 4 - 3 2 - 4 3 - 2 3 - 4 2 - 4 2 - 3 4 - 3 4 - 2 3 - 2 4 - 3 2 - 4 2 - 3 4 - 3 1 - 4 1 - 2 5 - 1 4 - 2 5 - 4 5 - 2 4 - 2 1 - 2 -------------------------------------------------------------------- -------------------------------------------------------------------- NO.2592 1 - 5 1 - 4 1 - 3 5 - 3 1 - 5 4 - 5 1 - 2 1 - 4 2 - 1 5 - 2 5 - 4 2 - 4 1 - 5 1 - 2 5 - 2 3 - 5 3 - 2 5 - 2 1 - 5 1 - 3 5 - 1 2 - 5 2 - 3 5 - 3 2 - 5 3 - 2 3 - 5 2 - 5 2 - 3 5 - 3 5 - 2 3 - 2 5 - 3 2 - 5 2 - 3 5 - 3 1 - 5 1 - 2 5 - 2 4 - 5 4 - 1 4 - 2 1 - 2 5 - 2全探索は無理ですが、(1-12)の場合 78 手
1-3 1-2 1-4 1-5 2-5 1-2 4-2 1-4 3-2 1-3 5-1 5-4 1-4 1-5 3-1 4-5 4-3 5-3 4-5 3-4 3-5 1-3 4-5 1-4 3-4 2-4 2-3 4-3 2-4 1-2 3-1 3-4 1-4 1-3 2-1 4-3 4-2 3-2 4-3 2-4 2-3 4-3 4-2 3-2 3-4 2-4 3-2 4-3 4-2 3-2 4-3 2-4 2-3 4-3 2-4 3-2 3-4 2-4 2-3 4-3 4-2 3-2 4-3 2-4 2-3 4-3 1-4 1-2 4-2 5-1 5-2 5-4 2-4 5-2 4-5 4-2 5-2 1-2手数は2,6,12,24,44,78,134,・・・
2nの場合
A(1)=2,A(2)=6,A(n)=A(n-1)+A(n-2)+2*(n-1)
この予想はかなり確度が高いと思います。
| Φ= | 1+ 2 |
2,6,12,24,44,78,134,226,376,620,1016,1658
÷2
1,3,6,12,22,39,67,113,188,310,508,829
これは数列サイトに掲載されています。
Lucas(n+1) - (n+1).
| C= | 1+ 2 | ,D= | 1- 2 |
この方がスッキリしていると思います。
Lucas数列と関係しています。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 24回
1→奇 数,2→空き2,3→空き1,4→偶 数,2→偶 数, 1→空き1,5→奇 数,6→空き2,5→最 初,2→奇 数, 4→空き2,2→空き2,5→偶 数,7→奇 数,5→奇 数, 8→偶 数,1→最 初,3→奇 数,1→奇 数,2→最 初, 4→空き1,6→偶 数,4→偶 数,2→偶 数,【問題2】
計算機によるしらみつぶしで確認した。
問題3解答はその結果である。
8種のカードの列位置は各5通りである。
各列において並び方は降順でなければならないので、各列へのカード配分に対して配置は1通りである。
よってカード配置のパターンは高々58で約36万である。
これは最近のPCにとっては、少ない探索範囲である。
実際、探索は1秒とかからなかった。
なお、探索ロジックはおよそ下図のイメージである。
まるの中の数字は手順の場合数である。
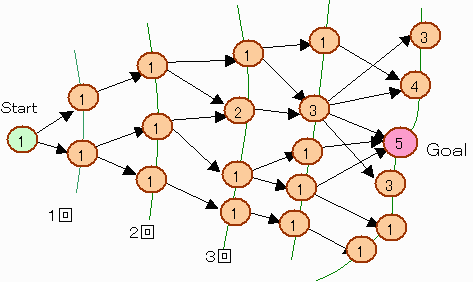
【問題3】 1044通り。
【おまけ】 最小は26回 228通り
1→奇 数,2→空き2,3→空き1,4→偶 数,2→偶 数, 5→空き2,3→空き2,6→空き1,1→空き2,7→奇 数, 2→最 初,4→空き1,2→空き1,8→偶 数,2→偶 数, 4→最 初,2→最 初,6→偶 数,2→空き1,4→偶 数, 1→最 初,2→偶 数,3→空き1,5→奇 数,3→奇 数, 1→奇 数,
◆ 問題へもどる
◆ 今週の問題へ