『今週の問題』第211回　解答

◆海外　ブリタ さんからの解答

【問題１】

n手まで進めた場合の数は、それぞれの手において選択肢が２つ（すなわち、２つの空き地のうち右を選ぶか左を選ぶか）しかないので、 2n通りになります。
上記の考えに基づき、最大13手目まで進めた場合（途中経過を含む）を全て検証する十進BASICプログラムは次の通りです。 

DIM CH$(1 TO 5)
DIM P$(1 TO 7)
DIM TE(1 TO 13)

LET SAIDAI=13

LET CH$(1)="A"
LET CH$(2)="B"
LET CH$(3)="C"
LET CH$(4)="D"
LET CH$(5)="E"

SUB CHGCHR(X$,X)

   FOR I1=1 TO 7
      IF P$(I1)=X$ THEN LET  Y1=I1
       
      IF X=0 THEN
         IF P$(8-I1)="*" THEN LET  Z1=8-I1
      ELSE
         IF P$(I1)="*" THEN LET  Z1=I1
      END IF
   NEXT I1    
    
   LET P$(Y1)="*"
   LET P$(Z1)=X$
    
END SUB


LET N=0
LET NO=1
LET TETL=2^SAIDAI-1

FOR I=0 TO TETL

   LET K=I
   FOR J=1 TO SAIDAI
      LET TE(J)=MOD(K,2)
      LET K=(K-TE(J))/2
   NEXT J 
    
   LET TEME=0
   LET P$(1)="A"
   LET P$(2)="B"
   LET P$(3)="C"
   LET P$(4)="D"
   LET P$(5)="E"
   LET P$(6)="*"
   LET P$(7)="*"
        
   DO
    
      LET TEME=TEME+1
      LET CH=MOD(TEME-1,5)+1
      CALL CHGCHR(CH$(CH),TE(TEME))
       
      LET JUDGE=0
      IF TEME>=SAIDAI THEN LET  JUDGE=1
      LET  CHTL$=P$(1)&P$(2)&P$(3)&P$(4)&P$(5)&P$(6)&P$(7)
      IF CHTL$="EDCBA**" THEN LET  JUDGE=2
       
   LOOP UNTIL JUDGE>0 
    
   IF JUDGE=2 THEN
      PRINT NO;": ";TEME;"手: ";
      FOR M=1 TO TEME
         IF TE(M)=0 THEN PRINT "左 "; ELSE PRINT "右 ";
      NEXT M 
      PRINT
      LET NO=NO+1
   END IF
    
NEXT I 

END
この結果は次の通りです。
 1 :  13 手: 左 右 右 左 左 左 右 右 左 左 右 右 左 
 2 :  13 手: 右 右 右 左 左 左 右 右 左 左 右 右 左 
 3 :  13 手: 左 右 右 左 右 左 右 右 左 左 右 右 左 
 4 :  13 手: 右 右 右 左 右 左 右 右 左 左 右 右 左
従って、最短の手数は13手となります。

【問題２】

十進BASICを走らせた結果、以下の通り最小手は21手、42通りです。 

  1 :  21 手: 左 右 右 左 右 右 右 右 左 左 左 右 右 左 右 左 左 左 左 左 左 
  2 :  21 手: 右 右 右 左 右 右 右 右 左 左 左 右 右 左 右 左 左 左 左 左 左 
  3 :  21 手: 左 左 左 右 右 右 右 右 右 右 左 右 右 左 右 左 左 左 左 左 左 
  4 :  21 手: 右 左 左 右 右 右 右 右 右 右 左 右 右 左 右 左 左 左 左 左 左 
  5 :  21 手: 左 右 右 左 左 右 左 右 左 左 左 右 右 右 右 左 左 左 左 左 左 
  6 :  21 手: 右 右 右 左 左 右 左 右 左 左 左 右 右 右 右 左 左 左 左 左 左 
  7 :  21 手: 左 右 右 左 右 右 左 右 左 左 左 右 右 右 右 左 左 左 左 左 左 
  8 :  21 手: 右 右 右 左 右 右 左 右 左 左 左 右 右 右 右 左 左 左 左 左 左 
  9 :  21 手: 左 右 右 左 左 右 左 右 右 左 左 右 右 右 右 左 左 左 左 左 左 
 10 :  21 手: 右 右 右 左 左 右 左 右 右 左 左 右 右 右 右 左 左 左 左 左 左 
 11 :  21 手: 左 右 右 左 右 右 左 右 右 左 左 右 右 右 右 左 左 左 左 左 左 
 12 :  21 手: 右 右 右 左 右 右 左 右 右 左 左 右 右 右 右 左 左 左 左 左 左 
 13 :  21 手: 左 左 左 右 左 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 14 :  21 手: 右 左 左 右 左 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 15 :  21 手: 左 左 左 左 右 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 16 :  21 手: 右 左 左 左 右 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 17 :  21 手: 左 左 左 右 右 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 18 :  21 手: 右 左 左 右 右 右 左 右 右 右 左 右 右 右 右 左 左 左 左 左 左 
 19 :  21 手: 左 左 左 右 左 右 左 右 左 左 左 右 右 右 右 右 右 左 左 左 左 
 20 :  21 手: 右 左 左 右 左 右 左 右 左 左 左 右 右 右 右 右 右 左 左 左 左 
 21 :  21 手: 左 左 左 右 右 右 左 右 左 左 左 右 右 右 右 右 右 左 左 左 左 
 22 :  21 手: 右 左 左 右 右 右 左 右 左 左 左 右 右 右 右 右 右 左 左 左 左 
 23 :  21 手: 左 左 左 右 左 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 24 :  21 手: 右 左 左 右 左 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 25 :  21 手: 左 左 左 左 右 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 26 :  21 手: 右 左 左 左 右 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 27 :  21 手: 左 左 左 右 右 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 28 :  21 手: 右 左 左 右 右 右 左 右 左 左 右 右 右 右 右 右 右 左 左 左 左 
 29 :  21 手: 左 右 右 左 右 右 左 右 左 左 左 左 左 右 右 左 左 左 右 右 左 
 30 :  21 手: 右 右 右 左 右 右 左 右 左 左 左 左 左 右 右 左 左 左 右 右 左 
 31 :  21 手: 左 右 右 左 右 右 右 右 左 左 左 左 左 右 右 左 左 左 右 右 左 
 32 :  21 手: 右 右 右 左 右 右 右 右 左 左 左 左 左 右 右 左 左 左 右 右 左 
 33 :  21 手: 左 左 左 右 右 右 左 右 右 右 左 左 左 右 右 左 左 左 右 右 左 
 34 :  21 手: 右 左 左 右 右 右 左 右 右 右 左 左 左 右 右 左 左 左 右 右 左 
 35 :  21 手: 左 左 左 右 右 右 右 右 右 右 左 左 左 右 右 左 左 左 右 右 左 
 36 :  21 手: 右 左 左 右 右 右 右 右 右 右 左 左 左 右 右 左 左 左 右 右 左 
 37 :  21 手: 左 左 左 左 左 左 右 右 右 右 左 右 右 右 右 左 左 左 右 右 左 
 38 :  21 手: 右 左 左 左 左 左 右 右 右 右 左 右 右 右 右 左 左 左 右 右 左 
 39 :  21 手: 左 左 左 右 右 右 左 右 左 左 左 左 左 右 右 右 右 左 右 右 左 
 40 :  21 手: 右 左 左 右 右 右 左 右 左 左 左 左 左 右 右 右 右 左 右 右 左 
 41 :  21 手: 左 左 左 左 左 左 右 右 左 左 右 右 右 右 右 右 右 左 右 右 左 
 42 :  21 手: 右 左 左 左 左 左 右 右 左 左 右 右 右 右 右 右 右 左 右 右 左

◆滋賀県　松尾 さんからの解答

【問題１】

以下のように動かします。
13手必要です。
(以下、途中経過はＮ手づつ進めた状態を示します。) 

( 0)ＡＢＣＤＥ＊＊
( 5)ＤＣ＊Ｅ＊ＡＢ
(10)ＥＤＡ＊＊ＢＣ
(13)ＥＤＣＢＡ＊＊
【問題２】

以下のように動かします。21手必要です。 

( 0) ＡＢＣＤＥＦ＊＊
( 6) ＤＣ＊ＥＦ＊ＡＢ
(12) ＥＤＣ＊＊ＡＢＦ
(18) ＦＥＤＢＡ＊Ｃ＊
(21) ＦＥＤＣＢＡ＊＊
【問題３】

Ｎ=15までやってみました。
これが最短手数かは分かりませんが、方法は、

(1) 1巡目、ＡＢを右の空いているマス目に入れ、ＣＤをＡＢが動いた後のマス目に入れます。
2巡目に動かせるように、Ａの左とＣの右に空のマス目がくるようにします。

(2) 2巡目以降、Ａを1個づつ左に、Ｃを1個づつ右に移動していきます。
Ｃの左側には文字が順に並ぶようにしておきます。

(3) ＡとＣの間に空のマス目が無くなったら、Ａ、Ｂ、Ｃの位置に注意しながら、右に動かして、完成します。 

Ｎ=7
( 0) ＡＢＣＤＥＦＧ＊＊
( 7) ＤＣ＊ＥＦＧ＊ＡＢ
(14) ＥＤＣ＊Ｇ＊ＡＢＦ
(21) ＦＥＤＣ＊ＡＢ＊Ｇ
(28) ＧＦＥＤＣＢ＊Ａ＊
(29) ＧＦＥＤＣＢＡ＊＊

Ｎ=8
( 0) ＡＢＣＤＥＦＧＨ＊＊
( 8) ＤＣ＊ＥＦＧＨ＊ＡＢ
(16) ＥＤＣ＊ＧＨ＊ＡＢＦ
(24) ＦＥＤＣ＊＊ＡＢＨＧ
(32) ＧＦＥＤＢＡ＊Ｃ＊Ｈ
(40) ＨＧＦＥＤＣＢ＊Ａ＊
(41) ＨＧＦＥＤＣＢＡ＊＊

Ｎ=9
( 0) ＡＢＣＤＥＦＧＨＩ＊＊
( 9) ＤＣ＊ＥＦＧＨＩ＊ＡＢ
(18) ＥＤＣ＊ＧＨＩ＊ＡＢＦ
(27) ＦＥＤＣ＊Ｉ＊ＡＢＨＧ
(36) ＧＦＥＤＣ＊ＡＢ＊ＩＨ
(45) ＨＧＦＥＤＣＢ＊Ａ＊Ｉ
(54) ＩＨＧＦＥＤＣＢ＊Ａ＊
(55) ＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=10
( 0) ＡＢＣＤＥＦＧＨＩＪ＊＊
(10) ＤＣ＊ＥＦＧＨＩＪ＊ＡＢ
(20) ＥＤＣ＊ＧＨＩＪ＊ＡＢＦ
(30) ＦＥＤＣ＊ＩＪ＊ＡＢＨＧ
(40) ＧＦＥＤＣ＊＊ＡＢＪＩＨ
(50) ＨＧＦＥＤＣＡＢ＊＊ＪＩ
(60) ＪＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=11
( 0) ＡＢＣＤＥＦＧＨＩＪＫ＊＊
(11) ＤＣ＊ＥＦＧＨＩＪＫ＊ＡＢ
(22) ＥＤＣ＊ＧＨＩＪＫ＊ＡＢＦ
(33) ＦＥＤＣ＊ＩＪＫ＊ＡＢＨＧ
(44) ＧＦＥＤＣ＊Ｋ＊ＡＢＪＩＨ
(55) ＨＧＦＥＤＣ＊ＡＢ＊ＫＪＩ
(66) ＩＨＧＦＥＤＣＢ＊Ａ＊ＫＪ
(77) ＫＪＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=12
( 0) ＡＢＣＤＥＦＧＨＩＪＫＬ＊＊
(12) ＤＣ＊ＥＦＧＨＩＪＫＬ＊ＡＢ
(24) ＥＤＣ＊ＧＨＩＪＫＬ＊ＡＢＦ
(36) ＦＥＤＣ＊ＩＪＫＬ＊ＡＢＨＧ
(48) ＧＦＥＤＣ＊ＫＬ＊ＡＢＪＩＨ
(60) ＨＧＦＥＤＣ＊＊ＡＢＬＫＪＩ
(72) ＩＨＧＦＥＤＣＡＢ＊＊ＬＫＪ
(84) ＫＪＩＨＧＦＥＤＣＢＡ＊＊Ｌ
(96) ＬＫＪＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=13
(  0) ＡＢＣＤＥＦＧＨＩＪＫＬＭ＊＊
( 13) ＤＣ＊ＥＦＧＨＩＪＫＬＭ＊ＡＢ
( 26) ＥＤＣ＊ＧＨＩＪＫＬＭ＊ＡＢＦ
( 39) ＦＥＤＣ＊ＩＪＫＬＭ＊ＡＢＨＧ
( 52) ＧＦＥＤＣ＊ＫＬＭ＊ＡＢＪＩＨ
( 65) ＨＧＦＥＤＣ＊Ｍ＊ＡＢＬＫＪＩ
( 78) ＩＨＧＦＥＤＣ＊ＡＢ＊ＭＬＫＪ
( 91) ＪＩＨＧＦＥＤＣＢ＊Ａ＊ＭＬＫ
(104) ＬＫＪＩＨＧＦＥＤＣＢＡ＊Ｍ＊
(117) ＭＬＫＪＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=14
(  0) ＡＢＣＤＥＦＧＨＩＪＫＬＭＮ＊＊
( 14) ＤＣ＊ＥＦＧＨＩＪＫＬＭＮ＊ＡＢ
( 28) ＥＤＣ＊ＧＨＩＪＫＬＭＮ＊ＡＢＦ
( 42) ＦＥＤＣ＊ＩＪＫＬＭＮ＊ＡＢＨＧ
( 56) ＧＦＥＤＣ＊ＫＬＭＮ＊ＡＢＪＩＨ
( 70) ＨＧＦＥＤＣ＊ＭＮ＊ＡＢＬＫＪＩ
( 84) ＩＨＧＦＥＤＣ＊＊ＡＢＮＭＬＫＪ
( 98) ＪＩＨＧＦＥＤＣＡＢ＊＊ＮＭＬＫ
(112) ＬＫＪＩＨＧＦＥＤＣＢＡ＊＊ＮＭ
(126) ＮＭＬＫＪＩＨＧＦＥＤＣＢＡ＊＊

Ｎ=15
(  0) ＡＢＣＤＥＦＧＨＩＪＫＬＭＮＯ＊＊
( 15) ＤＣ＊ＥＦＧＨＩＪＫＬＭＮＯ＊ＡＢ
( 30) ＥＤＣ＊ＧＨＩＪＫＬＭＮＯ＊ＡＢＦ
( 45) ＦＥＤＣ＊ＩＪＫＬＭＮＯ＊ＡＢＨＧ
( 60) ＧＦＥＤＣ＊ＫＬＭＮＯ＊ＡＢＪＩＨ
( 75) ＨＧＦＥＤＣ＊ＭＮＯ＊ＡＢＬＫＪＩ
( 90) ＩＨＧＦＥＤＣ＊Ｏ＊ＡＢＮＭＬＫＪ
(105) ＪＩＨＧＦＥＤＣ＊ＡＢ＊ＯＮＭＬＫ
(120) ＫＪＩＨＧＦＥＤＣＢ＊Ａ＊ＯＮＭＬ
(135) ＭＬＫＪＩＨＧＦＥＤＣＢＡ＊＊ＯＮ
(150) ＯＮＭＬＫＪＩＨＧＦＥＤＣＢＡ＊＊
Ｎ=15までしか確認してませんが、これ以上の個数でも、同じ手順で可能だと思われます。

手数ですが、Ｎ=10以上の場合で考えます。Ｃの位置に注目すると、

1) 2巡目以降、Ａ，Ｂに出会うまでの回数を調べます。
1巡目を終えたとき、Ａ，Ｃの間に Ｎ-2 文字の距離があり、1巡するごとに2個近づくので、出会うまでに
roundup((N-2)÷2) 巡 ( roundup は切り上げ )必要になります。
これを i とします。
出会ったとき、Ｃは右から2 + i の位置にあります。

2) その後、2個づつ右に移動します。
左から N-2 個の位置にくる巡数、
roundup(( (N-2)-(2+i) ) ÷2 ) 巡 で完成です。

3) 結局、必要な巡の数は、

最初の1巡 = 1
Ａ、Ｂと出会うまで = roundup((N-2)÷2) = i
左から N-2 の位置にくるまで = roundup(( (N-2)-(2+i) )÷2)

の合計です。
これに文字の数=Ｎをかけた答が手数です。

◆広島県　清川　育男 さんからの解答

【問題１】 

 13手
( 1)＊ＢＣＤＥＡ＊
( 2)＊＊ＣＤＥＡＢ
( 3)＊Ｃ＊ＤＥＡＢ
( 4)ＤＣ＊＊ＥＡＢ
( 5)ＤＣＥ＊＊ＡＢ
( 6)ＤＣＥＡ＊＊Ｂ
( 7)ＤＣＥＡ＊Ｂ＊
( 8)Ｄ＊ＥＡ＊ＢＣ
( 9)＊ＤＥＡ＊ＢＣ
(10)ＥＤ＊Ａ＊ＢＣ
(11)ＥＤ＊＊ＡＢＣ
(12)ＥＤ＊ＢＡ＊Ｃ
(13)ＥＤＣＢＡ＊＊

( 1)＊ＢＣＤＥＡ＊
( 2)＊＊ＣＤＥＡＢ
( 3)＊Ｃ＊ＤＥＡＢ
( 4)ＤＣ＊＊ＥＡＢ
( 5)ＤＣ＊Ｅ＊ＡＢ
( 6)ＤＣＡＥ＊＊Ｂ
( 7)ＤＣＡＥ＊Ｂ＊
( 8)Ｄ＊ＡＥ＊ＢＣ
( 9)＊ＤＡＥ＊ＢＣ
(10)ＥＤＡ＊＊ＢＣ
(11)ＥＤ＊＊ＡＢＣ
(12)ＥＤ＊ＢＡ＊Ｃ
(13)ＥＤＣＢＡ＊＊

( 1)＊ＢＣＤＥ＊Ａ
( 2)＊＊ＣＤＥＢＡ
( 3)＊Ｃ＊ＤＥＢＡ
( 4)ＤＣ＊＊ＥＢＡ
( 5)ＤＣＥ＊＊ＢＡ
( 6)ＤＣＥＡ＊Ｂ＊
( 7)ＤＣＥＡ＊＊Ｂ
( 8)Ｄ＊ＥＡ＊ＣＢ
( 9)＊ＤＥＡ＊ＣＢ
(10)ＥＤ＊Ａ＊ＣＢ
(11)ＥＤ＊＊ＡＣＢ
(12)ＥＤ＊ＢＡＣ＊
(13)ＥＤＣＢＡ＊＊

( 1)＊ＢＣＤＥ＊Ａ
( 2)＊＊ＣＤＥＢＡ
( 3)＊Ｃ＊ＤＥＢＡ
( 4)ＤＣ＊＊ＥＢＡ
( 5)ＤＣ＊Ｅ＊ＢＡ
( 6)ＤＣＡＥ＊Ｂ＊
( 7)ＤＣＡＥ＊＊Ｂ
( 8)Ｄ＊ＡＥ＊ＣＢ
( 9)＊ＤＡＥ＊ＣＢ
(10)ＥＤＡ＊＊ＣＢ
(11)ＥＤ＊＊ＡＣＢ
(12)ＥＤ＊ＢＡＣ＊
(13)ＥＤＣＢＡ＊＊
【問題２】

　21 手 
( 1)＊ＢＣＤＥＦＡ＊
( 2)Ｂ＊ＣＤＥＦＡ＊
( 3)ＢＣ＊ＤＥＦＡ＊
( 4)ＢＣＤ＊ＥＦＡ＊
( 5)ＢＣＤＥ＊ＦＡ＊
( 6)ＢＣＤＥＦ＊Ａ＊
( 7)ＢＣＤＥＦ＊＊Ａ
( 8)＊ＣＤＥＦ＊ＢＡ
( 9)Ｃ＊ＤＥＦ＊ＢＡ
(10)ＣＤ＊ＥＦ＊ＢＡ
(11)ＣＤ＊＊ＦＥＢＡ
(12)ＣＤ＊Ｆ＊ＥＢＡ
(13)ＣＤ＊ＦＡＥＢ＊
(14)ＣＤ＊ＦＡＥ＊Ｂ
(15)＊Ｄ＊ＦＡＥＣＢ
(16)＊＊ＤＦＡＥＣＢ
(17)＊ＥＤＦＡ＊ＣＢ
(18)ＦＥＤ＊Ａ＊ＣＢ
(19)ＦＥＤ＊＊ＡＣＢ
(20)ＦＥＤ＊ＢＡＣ＊
(21)ＦＥＤＣＢＡ＊＊
42通り

【問題３】

　空白　２箇所

　３個　　５手
　４個　　６手
　５個　１３手
　６個　２１手
　７個　２５手
　８個　２８手

予想

1,1,1,2,3,3,3,4,5,5,5

2個　　2*1+2/2=3 **
3個　　3*1+(3+1)/2=5 **
4個　　4*1+4/2=6 **
5個　　5*2+(5+1)/2=13 **
6個　　6*3+6/2=21 **
7個　　7*3+(7+1)/2=25 **
8個　　8*3+8/2=28 **
9個　　9*4+(9+1)/2=41 *
10個　 10*5+10/2=55

A(1)=0,A(2)=1,A(3)=1
A(n)=A(n-1)-A(n-2)+A(n-3)+1

B(n)=n*A(n)+ceiling(n/2) ，n≧2

 B(2)=3    *
 B(3)=5    *
 B(4)=6    *
 B(5)=13   *
 B(6)=21   *
 B(7)=25   *
 B(8)=28   *
 B(9)=41   *
 B(10)=55  ?
 B(11)=61  ?
 B(12)=66  ?
 B(13)=85  ?
B(10)-B(13) が確定すれば、予想が成立する可能性は高いと思われます。
また最後からのｎ手は１通りで、綺麗な規則性がみられます。

予想はほぼ間違いなさそうです。 

9個
 41 手
 10  11  2  3  1  5  6  7  8  9  10  11  4  3  2  1  6  7  8  5  10  11  4  3  2  1  9  7  6  5    10  11  4  3  2  1  9  8  7  6  5

10個
 55 手
 11  12  2  3  1  4  6  7  8  9  5  11  12  2  3  1  10  6  7  8  9  5  11  12  4  3  2  1  10  7  8  6  5  11  12  4  3  2  1  10  9  8  7  6  11  5  4  3  2  1  10  9  8  7  6

◆愛知県　Y.M.Ojisan　さんからの解答

【問題１】

最短は１３回

( 1)＊ＢＣＤＥ＊Ａ
( 2)＊＊ＣＤＥＢＡ
( 3)＊Ｃ＊ＤＥＢＡ
( 4)ＤＣ＊＊ＥＢＡ
( 5)ＤＣＥ＊＊ＢＡ
( 6)ＤＣＥＡ＊Ｂ＊
( 7)ＤＣＥＡ＊＊Ｂ
( 8)Ｄ＊ＥＡ＊ＣＢ
( 9)＊ＤＥＡ＊ＣＢ
(10)ＥＤ＊Ａ＊ＣＢ
(11)ＥＤ＊＊ＡＣＢ
(12)ＥＤ＊ＢＡＣ＊
(13)ＥＤＣＢＡ＊＊
 

【問題２】

可能であって　最短は２１回

( 1)＊ＢＣＤＥＦＡ＊
( 2)Ｂ＊ＣＤＥＦＡ＊
( 3)ＢＣ＊ＤＥＦＡ＊
( 4)ＢＣＤ＊ＥＦＡ＊
( 5)ＢＣＤＥ＊ＦＡ＊
( 6)ＢＣＤＥＦ＊Ａ＊
( 7)ＢＣＤＥＦ＊＊Ａ
( 8)＊ＣＤＥＦ＊ＢＡ
( 9)＊＊ＤＥＦＣＢＡ
(10)＊Ｄ＊ＥＦＣＢＡ
(11)ＥＤ＊＊ＦＣＢＡ
(12)ＥＤ＊Ｆ＊ＣＢＡ
(13)ＥＤ＊ＦＡＣＢ＊
(14)ＥＤ＊ＦＡＣ＊Ｂ
(15)ＥＤ＊ＦＡ＊ＣＢ
(16)Ｅ＊ＤＦＡ＊ＣＢ
(17)＊ＥＤＦＡ＊ＣＢ
(18)ＦＥＤ＊Ａ＊ＣＢ
(19)ＦＥＤ＊＊ＡＣＢ
(20)ＦＥＤ＊ＢＡＣ＊
(21)ＦＥＤＣＢＡ＊＊
 

【問題３】

一般にＮ個の文字を並び替えることはできる。
最小性は証明できていないが、下記手数で並び替えが可能であり、これが最小値と予想される。

ｎ＝４ｍ−１のとき、 ｎ２＋１
２
ｎ＝４ｍのとき、 ｎ２−ｎ
２
ｎ＝４ｍ＋１のとき、 ｎ２＋１
２
ｎ＝４ｍ＋２のとき、 ｎ２＋ｎ
２


具体的値を一部下表に示す。

表１　ＰＣによるしらみつぶしにより最小であることを確認した手数。
ｎ ２ ３ ４ ５ ６ ７ ８
手数 ３ ５ ６ １３ ２１ ２５ ２８


表２　少なくとも可能な手数であって最小と予想する手数。
ｎ ９ １０ １１ １２ １３ １４ １５
手数 ４１ ５５ ６１ ６６ ８５ １０５ １１３


【証明】

【視点の置き換え】

　まず、マスにＡのところを０番としてｎ＋１番まで順に背番号をつけます。
また別に、下図のような　２×（ｎ＋２）個の待ち行列のマス列を作ります。
なお、文字Ｙ，Ｚは一般にｎ−１番目、ｎ番目の文字の代用表記です。
また、空白も一つの文字とみなしΦで表記します。

　すると、一回の操作は、文字のほうのグループではＡ〜Ｚの環状シフト置換（長さｎ）であることがわかります（黒矢印）。
一方背番号の方は、待ち行列の　ｎ　を通るか　ｎ＋１　を通るかの２種類の長さｎ＋１の環状シフト置換であることがわかります（黒＋赤矢印　または　黒＋赤矢印）。

 

 　文字のグループは操作が限られており、かつ環状シフトなのでその順は不変です。
従って、順を逆転させるにはマス背番号の方を換えれるしかないことがわかります。

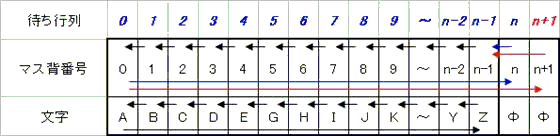
　実際、待ち行列のｎ番とｎ＋１番を用いて任意の追い越しを行うことが可能なので、それは可能です。
次に文字と番号を合わせる必要がありますが、文字の周期ｎとマス番号の周期ｎ＋１は互いに素ですから、何回か環状シフトをまわせば、合わせる（Ｚを０番にする）ことが可能です。

即ち任意のｎで可能です。

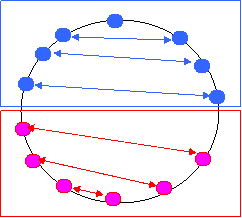
【最小の限界】

　下図に示すように、円環状に配置されている背番号の順を逆にするには、背番号をほぼ半分ずつの２グループにわけるのが最も手数が少ないと言えます。
　一周につき各グループ１個ずつ２個交換できるので、
少なくとも[ ｎ−１
２		]周は必要です。

１周につき手数はｎ＋１は必要であり、かつ交換を行うためにはΦを一度２個とも周回に出さなければならないため、最後に＋１回が必要です。

即ち、どんなに少なくても
　[ ｎ−１
２		]*(ｎ＋１)＋１　回は手数が必要です。

そしてさらに文字Ａと背番号ｎ−１が同じ位置でなければなりません。


 

【手順】

以下ｎの４を法とする剰余で分類して手順を示します。

（１）　ｎ＝４ｍの場合

この場合
　[ ｎ−１
２		]*(ｎ＋１)＋１
＝（ ｎ
２		−１）（ｎ＋１）＋１
＝ ｎ（ｎ−１）
２		　が最小です。

また　 ｎ（ｎ−１）
２		≡２ｍ　　ｍｏｄ　ｎ　　です。

したがって、この値で丁度文字Ａと背番号ｎ−１が最後に一致するには、２グループの境界が、中央のとことろに来る必要があります。

実際それは可能であって、

（１−１）　下図のように　
ｍ＋1個　ｍ−1個　ｍ＋1個　ｍ−1個　の４グループに分けます。
それぞれα、β、γ、δとよびます。
まず、ｍ−１周を費やして、αとγの２グループのｍ個をそれぞれ逆順に並べ換ます。
また、δのｍ−１個を並びの先頭に逆順にして移動させます。



（１−２）次にさらにｍ−１周を費やして、δをαの後ろに入れ、βを逆順にしてαの前に移動させます。



（１−３）最後にほぼ１周して、αとガンマに残った１個ずつを移動させ完成させます。
このとき輪は丁度２ｍずれています。

　　　

以上全部で２ｍ−１周であり最小の周回数です。


（２）　ｎ＝４ｍ−１の場合

この場合
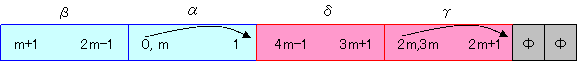
　[ ｎ−１
２		]*(ｎ＋１)＋１
＝ （ｎ−１）（ｎ＋１）
２		＋１
＝ ｎ２＋１
２		　が最小です。

また　 ｎ２＋１
２		≡２ｍ　　ｍｏｄ　ｎ　です。

　従って、ｍ個　ｍ−1個　ｍ＋１個　ｍ−1個　の４グループに分け、（１）とほとんど同じ手順で、（１−３）でのαの移動のみ行わなければ、丁度２ｍずれた位置で終了できます。
下図に（２−３）相当の図のみ示します。

　　　


（３）　ｎ＝４ｍ＋１の場合

この場合　
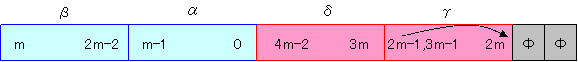
　[ ｎ−１
２		]*(ｎ＋１)＋１
＝ （ｎ−１）（ｎ＋１）
２		＋１
＝ ｎ２＋１
２		　が最小です。

また　 ｎ２＋１
２		≡２ｍ＋１　　ｍｏｄ　ｎ　です。


従って、ｍ＋１個　ｍ−1個　ｍ＋１個　ｍ個　の４グループに分け、（１）とほとんど同じ手順で、（１−３）の後にもう一周してγの最後の一個をδの前に移動すれば、丁度２ｍ＋１ずれた位置で終了できます。
下図に（３−４）相当の図のみ示します。




（４）　ｎ＝４ｍ＋２の場合

この場合
　[ ｎ−１
２		]*(ｎ＋１)＋１
＝（ ｎ
２		−１）（ｎ＋１）＋１
＝ ｎ（ｎ−１）
２		　が最小です。

また　 ｎ（ｎ−１）
２		≡２ｍ＋１　　ｍｏｄ　ｎ　です。

　しかし、最小のｍ周では、丁度２ｍ＋１ずらすことが偶奇性からできないようです（未証明）。
もう一周すれば、１だけずらせて合わせることが可能です。
　このとき、逆順化は完成しており、入れ替えは不要なので、Φを追い出すのは１個だけでよく、余分の手数はｎ＋１ではなく、ｎで回すことが可能です。

従って、手数は　（２ｍ＋１）×（ｎ＋１）＝ ｎ２＋ｎ
２		　です。

ずれは、　２ｍ＋１のままでよいです。
以下手順を示します。

（４−１）　下図のように　ｍ＋1個　ｍ個　ｍ＋1個　ｍ個　の４グループに分けます。

まず、ｍ周を費やして、αとγの２グループのｍ＋１個をそれぞれ逆順にならべ、δのｍ個を列の先頭に逆順にして移動させます。



（４−２）次にさらにｍ周を費やして　δをαの後ろに入れ、βの２ｍ番を残して逆順にしてαの前に移動させます。



（４−３）　最後にβの２ｍ番を１周以上して、先頭に移動させて終了します。

　

 以上全部で２ｍ＋１周であり、最小の周回数＋１です。
 

【感想】

最小性の証明が残念ながらできませんでした。なにか別のアプローチが必要でした。
 

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる