 悢妛偺晹壆傊傕偳傞丅
悢妛偺晹壆傊傕偳傞丅仧惷壀導丂儓僢僔乕 偝傫偐傜偺夝摎丅
亂栤戣侾亃
侾俇杮
亂栤戣俀亃
栚惙偺悢偼
侾亄侾亄俀亄俀亄俁亄俁亄係亄係亄俆亄俆亄俇亄俇亄俈亄俈亄俉亄俉亖俈俀妏偼丂侾俆屄
俈俀亄侾俆亖俉俈
丂丂丂俉俈昩乮侾暘俀俈昩)
亂栤戣俁亃
俀値斣栚偺妏偵拝偔帪娫偼丄栚惙偺悢偑
丂俀亊乮侾亄俀亄俁亄丒丒丒亄値)亖値乮値亄侾)
妏偑俀値亅侾屄
傛偭偰丄乮値亄侾)乮値亄俀)亅俁丂昩屻
俀俉斣栚偺妏乮値亖侾係)偵拝偔偺偑丂侾俆亊侾俇亅俁亖俀俁俈丂昩屻
侾昩偐偐偭偰岦偒傪曄偊丄傕偆俀栚惙恑傓偲丄俀係侽昩乮係暘)偲側傞丅
偙偺嬫娫偺妏偐傜妏偺挿偝偼侾俆栚惙側偺偱丄師偺妏傑偱偼侾俁昩丅
仧愇愳導丂Takashi 偝傫偐傜偺夝摎丅
亙嘥亜揰俙傪尨揰丄塃曽岦偵倶幉丄忋曽岦偵倷幉傪庢傞丅
尨揰偐傜丄忋偵侾倣丄塃偵侾倣丄壓偵俀倣丄嵍偵俀倣丄堏摦偡傞偲揰乮-1,-1)偵摓拝偡傞丅
値廃栚偵揰乮1-n,1-n)偐傜揰乮-n,-n)傑偱堦廃偡傞偺偵昁梫側嫍棧俴(n)偼丄
俴(n)亖乮2n-1)亄乮2n-1)亄2値亄2値亖8値-2
俛乮-4,-4)偵摓拝偡傞偺偵偐偐傞嫍棧俴偼丄
| 俴亖 | 4 儼 n=1 | 俴(n) |
丂亖俈俀倣
亙嘦亜揰俙偐傜揰俛偵堏摦偟偰忋岦偒偵側傞傑偱偺娫偵嬋傞夞悢傪峫偊傞偲丄侾廃摉傝丄係夞
傛偭偰丄揰俛偵摓拝偡傞偺偵偐偐傞帪娫俿偼丄
俿亖俴亊侾亄乮係亊係亅侾)亊侾
丂亂嵟屻偺廃偱揰俛偵拝偄偨帪丄忋岦偒偵側傞昁梫偑柍偄偺偱丄嬋傞夞悢亅侾亃丂亖侾暘俀俈昩
亙嘨亜揰俙乮0,0)偐傜揰俠n乮-n,-n)偵堏摦偟偰忋岦偒偵側傞偺偵昁梫側帪娫傪俿(m)偲偡傞偲丄
| 俿(m)亖 | m 儼 n=1 | 俴(n)亄係倣 |
丂亖係倣2亄俇倣
偙偙偱丄俿(7)亖俀俁俉偩偐傜丄係暘屻偼丄俈廃偟偨屻俀曕忋偵堏摦偟偰偄傞偐傜丄
忋岦偒偱揰乮-7,-5)偵偄傞丅
偦偙偐傜丄師偺妏乮-7,8)偵拝偔傑偱偵偐偐傞帪娫倲偼丄
倲亖俉亅乮亅俆)亖侾俁昩
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎丅
亂栤戣侾亃
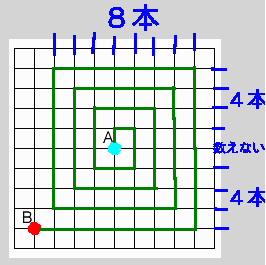
揰B偼揰A偐傜嵍偵係倣丄壓偵係倣偺埵抲偵偁傞丅
塓姫偒忬偵嬤偢偔偐傜丄
墶丂係亊俀亖俉丅丂廲丂係亊俀亖俉丅
捠夁偡傞捈慄偺杮悢偼丄
俉亄俉亖侾俇丅
摎偊丂侾俇杮丅
亂栤戣俀亃
墶丂侾亄俀亄俁亄係亄俆亄俇亄俈亄俉亖俁俇丅
廲丂侾亄俀亄俁亄係亄俆亄俇亄俈亄俉亖俁俇丅
俁俇亄俁俇亄乮侾俇亅侾)亖俈俀亄侾俆亖俉俈丅
摎偊丂俉俈昩丅
亂栤戣俁亃
捈慄偺杮悢丂侾丆俀丆俁丆係丆丂俆丆丂俇丆丂俈丆丏丏
梫偡傞帪娫丂侾丆俁丆俇丆俋丆侾俈丆俀俀丆俀俈丆丏丏
捈慄偺杮悢偲梫偡傞帪娫偺娭學
値亖俀倣亅侾丂倣2亄俀倣亅俀
値亖俀倣丂丂丂倣2亄俁倣亅侾
値亖俀俋偺偲偒丂倣亖侾俆
丂侾俆2亄俀亊侾俆亅俀
亖俀俀俆亄俁侽亅俀
亖俀俆俁
俀俆俁亅俀係侽亖侾俁
摎偊丂侾俁昩丅
偍傑偗
侾)
乮侾亄乮俀倣亅侾))乮俀倣亅侾)亄乮倣亅値)
亖係倣2亅倣亅値
摎偊丂係倣2亅倣亅値丅
俀)
| 捈慄偺杮悢 | 侾 | 俀 | 俁 | 係 |
| 埵抲 | 乮俇丆俆) | 乮俈丆俆) | 乮俈丆俈) | 乮俆丆俈) |
| 梫偡傞帪娫 | 侾 | 俁 | 俇 | 俋 |
仧垽昋導偺拞妛峑俁擭惗丂垻晹 偝傫偐傜偺夝摎丅
栤侾)侾俇杮
栤俀)
| 俶 | 昩 | 捀揰 |
| 侾 | 俀 | 侾 |
| 俀 | 俇 | 俁 |
| 俁 | 侾俀 | 俆 |
| 丗 | 丗 | 丗 |
忋偺傛偆偵側傞偺偱丄俶偲昩偼丄俶乮俶亄侾)
捀揰偼丄丂丂俀俶亅侾
傛偭偰丄俶乮俶亄侾)亄俀俶亅侾
丂俉亊俋亄侾俇亅侾亖俉俈
俉俈昩
栤俁)
俀係侽亖俶乮俶亄侾)亄俀俶亅侾
俀係侾亖俶乮俶亄俁)
侾係亊侾俈亖俀俁俉
曽岦揮姺偱侾昩
侾俆亅俀亖侾俁丂侾俁昩
仧孮攏導偺拞妛峑俁擭惗
丂僑儕儔乕儅儞偝傫丄儌儞僑儖儅儞偝傫丄懢揷 偝傫偐傜偺夝摎丅
亂栤戣侾亃
丂侾俇杮
姶憐摍
 乮懢揷丄俁擭丄彈巕)
乮懢揷丄俁擭丄彈巕)亂栤戣俀亃
丂俉俈昩
仧愇愳導丂暯揷榓峅 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俙偐傜俛傊恑傓傑偱侾曈偺挿偝偑偦傟偧傟
侾仺侾仺俀仺俀仺丏丏丏丏丏仺俉仺俉偲恑傫偱偄偔偺偱捈慄偺杮悢偼
俉亊俀亖侾俇杮偺捈慄傪恑傒傑偡丅
亂栤戣俀亃
傑偢曈偺挿偝偺憤崌寁傪媮傔傞偲
丂侾亄侾亄俀亄俀亄丏丏丏丏丏亄俉亄俉
亖俀亊{(俀亄俉)亄(俁亄俈)亄(係亄俇)亄(俆亄侾)}
亖俀亊(侾侽亄侾侽亄侾侽亄俇)
亖俀亊俁俇
亖俈俀丂偲側傝傑偡丅
丂師偵妏偺悢傪媮傔傑偡丅
侾曈偺挿偝偑侾仺侾丄俀仺俀丄丏丏丏偲偄偆傛偆偵摨偠挿偝偱曈偑曄傢傞偲偒偺妏偺悢偼俉偁傝傑偡丅
傑偨侾曈偺挿偝偑侾仺俀丄俀仺俁丄丏丏丏丏偲偄偆傛偆偵堘偆曈偺挿偝偱曈偑偐傢傞偲偒偺妏偺悢偼俈偁傝傑偡丅
廬偭偰媮傔傞妏偺悢偼俉亄俈亖侾俆偱偡丅
忋婰傛傝媮傔傞帪娫偼俈俀亄侾俆亖俉俈昩偱偡丅
亂栤戣俁亃
係暘亖係亊俇侽昩亖俀係侽昩偵偳偺抧揰偵偄傞偐媮傔偰傒傑偡丅
忋婰栤戣俀傪棙梡偟偰
(侾亄侾亄俀亄俀亄丏丏丏亄仜亄仜)亄(侾亄侾亄侾亄侾亄丏丏丏亄侾)亄(侾亄侾亄侾亄丏丏丏丏侾)亝俀係侽丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜屄丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜亅侾屄傪枮偨偡仜傪媮傔傞偲仜亖14偲側傝傑偡丅
侾曈偑侾係仺侾俆傊偺妏偱侾昩壛嶼偝傟傞偺偱俀係侽昩偱偼侾曈偑侾俆偺挿偝偺嵟弶偺曈偺俀倣恑傫偩偲偙傠偵偄傞偙偲偵側傝傑偡丅
丂(俀係侽亅俀俁俈亄侾亖俀)
廬偭偰丄師偺妏傑偱偵偐偐傞帪娫偼
侾俆亅俀亖侾俁昩偲側傝傑偡丅
偍傑偗乮侾)
倣亜値亜0側偺偱倣傪拞怱偵峫偊偰偄偔丅
傑偢傢偐傝傗偡偔値亖侾偲偟偰(杮摉偼壗偱傕傛偄偑)
倣亖侾,俀,俁,......偺抧揰偱偼媮傔傞抧揰俠偼昁偢侾曈偑俀倣偺嵟弶偺曈忋偵側傝傑偡丅
偩偐傜丄侾曈偑俀倣亅侾傑偱偺捈慄偺挿偝偺憤崌寁偼
丂{(侾亄侾)亄(俀亄俀)亄....亄(俀倣亅侾)亄(俀倣亅侾)}
亖俀亊(俀倣亅侾)丒俀倣乛俀
亖係倣2亅俀倣
崱偄傞抧揰偺侾曈偺挿偝偼俀倣偩偐傜敿暘偺挿偝偼倣偱
偦偙偐傜崅偝値偩偗忋偵忋偑偭偨抧揰偼倣亅値偱媮傔傜傟傞丅
廬偭偰丄抧揰俠傑偱偺嫍棧偼
丂係倣2亅俀倣亄倣亅値
亖係倣2-倣亅値偲側傞丅
姶憐
偙偺栤戣偼嵟弶恾宍偺栤戣偲偟偰峫偊偰偄傑偟偨偑悢帤偺楍偲偟偰峫偊傞偲揥奐偑尒偊偰偒傑偟偨丅
嵶偐側拲堄揰偑偁傞偺偱偐側傝擄偟偄偲巚偄傑偡丅
偍傑偗(俀)
俶亖婏悢偺偲偒
挿偝偺崌寁偼
丂{(侾亄侾)亄(俀亄俀)亄丏丏亄{(俶亅侾)乛俀}亄{(俶亅侾)乛俀}亄(俶亄侾)乛俀
亖丏丏丏丏丏丏
亖(俶亄侾)2乛係丒丒丒(俙)
偲側傞偺偱僗僞乕僩偐傜偺挿偝偑(俙)偺抧揰偵偄傑偡丅
傑偨妏偺崌寁偼(俶-1)側偺偱俙偐傜恑傫偩帪娫偼(俙)偵壛嶼偡傞偲
丂(俶亄侾)2乛係亄俶亅侾
亖丏丏丏丏
亖(俶2亄俇俶亅俁)乛係昩偱偡丅
俶亖嬼悢偺偲偒
挿偝偺崌寁偼
丂{(侾亄侾)亄(俀亄俀)亄丏丏亄(俶乛俀)亄(俶乛俀)
亖丏丏丏丏丏丏
亖(俶2亄俀俶)乛係丂丒丒丒(俛)
偲側傞偺偱僗僞乕僩偐傜偺挿偝偑(俛)偺抧揰偵偄傑偡丅
傑偨妏偺崌寁偼(俶-1)側偺偱俙偐傜恑傫偩帪娫偼(俛)偵壛嶼偡傞偲
丂(俶2亄俀俶)乛係亄俶亅侾
亖丏丏丏丏
亖(俶2亄俇俶亅係)乛係昩偱偡丅
偍傑偗(俁)
偙偺栤戣偼俿昩屻偵妏偵偄傞偐偳偆偐傢偐傜側偄偺偱岞幃偼摫偗傑偣傫偱偟偨偑丄埲壓偺梫椞偱捈慄偺杮悢偼媮傔傜傟傑偡丅
傑偢丄捈慄偺杮悢偲宱夁帪娫偺娭學傪挷傋傞偲
| 捈慄偺杮悢 | 宱夁帪娫 |
| 侾 | 侾丄俀(昩屻) |
| 俀 | 俁丄係 |
| 俁 | 俆丄俇丄俈 |
| 係 | 俉丄俋丄侾侽 |
| 俆 | 侾侾丄侾俀丄侾俁丄侾係 |
| 俇 | 侾俆丄侾俇丄侾俈丄侾俉 |
| 丗 | 丗 |
偲側傞偺偱捈慄偺杮悢傪偦傟偧傟侾偮偺僌儖乕僾偲峫偊偰偁傞悢(俿)偑梌偊傜傟偨帪偵俿偑偳偺僌儖乕僾偵懏偡傞偐傪媮傔傟偽捈慄偺杮悢偑傢偐傝傑偡丅
僌儖乕僾斣崋(俶)偑婏悢偺偲偒
僌儖乕僾偺愭摢偺悢偼
(俀亄俀)亄(俁亄俁)亄丏丏亄{(俶亄侾)乛俀}亄{(俶亄侾)乛俀}亄侾
亖丏丏丏丏丏丏丏
亖(俶2亄係俶亅侾)乛係
傑偨偙偺僌儖乕僾偺屄悢偼(俶亄俁)乛俀側偺偱
(俶2亄係俶亅侾)乛係亝俿亙(俶2亄係俶亅侾)乛係亄(俶亄俁)乛俀
幃傪娙扨偵偟偰
俶2亄係俶亅侾亝係俿亙俶2亄俇俶亄俆丒丒(俙)
傪枮偨偡惍悢傪傒偮偗傟偽傛偄偙偲偵側傞丅
僌儖乕僾斣崋(俶)偑嬼悢偺偲偒
僌儖乕僾偺愭摢偺悢偼
丂(俀亄俀)亄(俁亄俁)亄丏丏亄(俶乛俀)亄(俶乛俀)亄侾
亖丏丏丏丏丏丏丏
亖(俶2亄係俶)乛係
傑偨偙偺僌儖乕僾偺屄悢偼(俶亄俀)乛俀側偺偱
(俶2亄係俶)乛係亝俿亙(俶2亄係俶)乛係亄(俶亄俀)乛俀
幃傪娙扨偵偟偰
俶2亄係俶亝係俿亙俶2亄俇俶亄係丒丒丒(俛)
傪枮偨偡惍悢傪傒偮偗傟偽傛偄偙偲偵側傞丅
幚嵺偼僌儖乕僾斣崋偑傢偐傝傑偣傫偑椺偊偽俿亖侾侽侽偲偡傞偲
僌儖乕僾斣崋俶偑傕偟婏悢偲偡傞偲忋婰(俙)傪枮偨偡惍悢偼懚嵼偟側偄丅
俶亖侾俈偲偟偰傕
侾俈2亄係亊侾俈亅侾亝係侽侽亙侾俈2亄俇亊侾俈亄俆
俁俆俇亝係侽侽亙俁俋俇丂偲側傝懚嵼偟側偄丅
僌儖乕僾斣崋俶偑傕偟嬼悢偲偡傞偲忋婰(俛)傪枮偨偡惍悢偼偡傞丅
俶亖侾俉偲偡傞偲
侾俉2亄係亊侾俉亝係侽侽亙侾俉2亄俇亊侾俉亄係
俁俋俇亝係侽侽亙係俁俇丂偲側傝懚嵼偡傞丅
廬偭偰俿亖侾侽侽昩偺偲偒捈慄偼侾俉杮偲側傞丅
仧榓壧嶳導丂偨傑 偝傫偐傜偺夝摎丅
亂栤戣侾亃
揰B偼揰A偐傜壓偵4丄嵍偵4恑傫偩埵抲偵偁傞丅
儘儃僢僩偼廲偼忋亥忋丒丒丄墶偼塃顶塃丒丒偲恑傓偺偱廲丄墶偦傟偧傟偺捈慄偺悢偑嬼悢杮偺帪儘儃僢僩偼壓丄嵍偵恑傓丅
偙偙偱丄廲偺捈慄偩偗偱峫偊傞偲捈慄偺悢偑2n杮偺帪儘儃僢僩偼n栚惙傝壓偺埵抲偵偁傞丅
偮傑傝丄儘儃僢僩偑4栚惙傝壓偺埵抲偵棃傞偵偼
2亊4=8杮偺捈慄傪捠傞偙偲偵側傞丅
墶偺捈慄偱傕摨偠帠偑偄偊傞偺偱揰B偵摓拝偡傞傑偱
8+8=16杮偺捈慄傪恑傓丅
亂栤戣俀亃
廲丄墶偦傟偧傟捈慄偺悢偑1杮憹偊傞偲恑傓嫍棧傕1栚惙傝憹偊傞偺偱揰B偵拝偔傑偱廲丄墶偲傕偵
1+2+3+4+5+6+7+8=36栚惙傝恑傓丅
傑偨丄n杮偺捈慄偱n-1屄偺妏偑偱偒傞偺偱丄揰B偵拝偔傑偱
16-1=15杮偺妏傪捠傞丅
傛偭偰丄揰B偵拝偔傑偱偵偐偐傞帪娫偼
36+36+15=87昩偮傑傝1暘27昩偵側傞丅
亂栤戣俁亃
亂栤戣2亃傛傝丄廲n杮丄墶n杮偮傑傝2n杮偺捈慄傪恑傫偩帪丄恑傫偩嫍棧偼1乣n偺榓偺2攞偵側傝丄妏偺悢偼2n-1偵側傞丅
1乣n偺榓偼1/2n(n+1)偩偐傜2n杮偺捈慄傪恑傓偺偵偐偐傞帪娫偼
2亊1/2n(n+1)+2n-1=n(n+3)-1昩偵側傞丅
揰A傪弌敪偟偰偐傜4暘屻偺埵抲偼
n(n+3)-1亝240
n(n+3)亝241
0亙n亙15
偮傑傝丄2亊14=28杮偐傜2亊15=30杮偺娫偵偄傞丅
28杮偺捈慄傪恑傓偺偵偐偐傞帪娫偼14亊17-1=237昩丄
妏傪嬋偑傞偺偵1昩偐偐傞偐傜4暘屻偺埵抲偼偦偙偐傜廲偵2栚惙傝恑傫偩埵抲偱偁傞丅
廲偵14杮恑傫偩埵抲偐傜師偺妏傑偱偼15栚惙傝恑傑側偗傟偽側傜側偄偐傜丄
15-2=13栚惙傝丄偮傑傝13昩偐偐傞丅
仸n偼帺慠悢
仧嶉嬍導偺拞妛峑俁擭惗丂埨揷丂撧墰丂偝傫偐傜偺夝摎丅
亂栤戣侾亃
侾俇杮
亂栤戣俀亃
傑偢丄俙偐傜弌敪偟偨儘儃僢僩偑嵟弶偺妏傪嬋偑傞傑偱偑丄侾昩丅
岦偒傪曄偊傞偺偵丄侾昩丅
偁傢偣偰俀昩偐偐傝傑偡丅偙傟傪嬼悢偲偟傑偡丅
師偺妏傕嬼悢偱偡丅
師偺妏偼丄俀昩偐偐傝傑偡丅岦偒傪曄偊傞偺偵丄侾昩丅
偁傢偣偰俁昩丅偙傟傪婏悢偲偟傑偡丅
楍傪倃偲偡傞偲丄
嬼悢偺幃偼丄俀倃丂偲昞偣傑偡丅
婏悢偺幃偼丄俀倃亄侾偲昞偣傑偡丅
嬼悢偲婏悢偺幃偼俀偮偢偮偁傞偺偱丄
丂嬼悢偺幃偼丄係倃
丂婏悢偺幃偼丄係倃亄俀丂丂偲昞偣傞丅
| 丂 | 嬼悢 | 婏悢 | 崌寁 |
| 侾楍栚 | 係 | 俇 | 侾侽 |
| 俀楍栚 | 俉 | 侾侽 | 侾俉 |
| 俁楍栚 | 侾俀 | 侾係 | 俀俇 |
| 係楍栚 | 侾俇 | 侾俉 | 俁係 |
| 崌寁 | 係侽 | 係俉 | 俉俉 |
嵟屻偺妏搙傪嬋偑傜側偄偺偱丂侾傪堷偔偲摎偊偼丄俉俈偱偡丅
丂仧丂栤戣傊傕偳傞
丂仧丂崱廡偺栤戣傊
丂丂