◆愛知県 迷子の雄猫 さんからの解答
【ステップ1】
目標のカエルの配置から変換できる、中央が空きマスである配置を考える。
目標のカエルの配置の中央にかえるがいる場合には、中央から空きマスまでの経路上にいるかえるを順次ずらして、中央にかえるが居ない図(以下、途中図)に変形すると、中央が空きマスになる。
【ステップ2】
隣同士の蛙を入れかえる。
以下、基本図Sのかえるの番号で、それぞれの場所を表す。
0は中央とする。
●1と2を入れかえる場合
場所6にいる蛙6を0に移動,
場所4にいる蛙4を場所6に移動,
場所1にいる蛙1を場所4に移動,
場所2にいる蛙2を場所1に移動,
場所4にいる蛙1を場所2に移動,
場所6にいる蛙4を場所4に移動,
場所0にいる蛙6を場所6に移動
●3と4を入れかえる場合
場所6にいる蛙6を場所0に移動,
場所3にいる蛙3を場所6に移動,
場所4にいる蛙4を場所3に移動,
場所6にいる蛙3を場所4に移動,
場所0にいる蛙6を場所6に移動
上記と同様の手順で、中央が空いていれば、隣り合う蛙を入れかえることが出来る。
【ステップ3】
任意の位置の蛙を入れかえる。
どの2つの場所に対しても、中央を通らずに移動する経路が存在するから、以下のように、他の場所に影響を与えないで、任意の蛙を入れかえることが出来る。
1−A−B−C−D−E−2 A−1−B−C−D−E−2 A−B−1−C−D−E−2 A−B−C−1−D−E−2 A−B−C−D−1−E−2 A−B−C−D−E−1−2 A−B−C−D−E−2−1 A−B−C−D−2−E−1 A−B−C−2−D−E−1 A−B−2−C−D−E−1 A−2−B−C−D−E−1 2−A−B−C−D−E−1【ステップ4】
基本図を途中図経由で目標となる配置に変形する。
蛙1を正しい位置に、蛙2を正しい位置に・・・と順次入れかえれば、基本図から途中図には変形できる。
ステップ1と逆の手順で、途中図から目標のカエルの配置に変形できる。
よって、どのようなカエルの配置に対しても、基本図から移動する手順は存在する。
(証明終わり)
◆千葉県 菜花子 さんからの解答
【問題1】
【問題1−a】 180度回転
( 2)→( 5)→( 8)→(11)→( 5)→( 8)→(11)→( 2)→(12)→( 9)→ ( 6)→( 3)→( 9)→( 6)→( 3)→(12)→(10)→( 1)→( 4)→( 7)→ ( 1)→( 4)→( 7)→(10)→手数:24手
基本図Sの [1,4,7,10][2,5,8,11][3,6,9,12]を、それぞれ180度回転させる。
手順:
(1)各4匹のカエルのうち1匹を空きスペースに移動させておく。
(2)残り3匹のカエルを順に180度回転させる。
(3)空きスペースのカエルを移動させる。
手数:
(1)で、1手
(2)で、6手
(3)で、1手
以上を3グループそれぞれですると、合わせて24手
【問題1−b】 左右反転
( 6)→( 9)→( 8)→( 5)→( 9)→( 8)→( 5)→( 6)→( 2)→(11)→ (12)→( 3)→(11)→(12)→( 3)→( 2)→( 4)→(10)→( 4)→手数:19手
基本図Sの[3,2,12,11][5,6,8,9][4,10]を、それぞれ左右反転させる。
手順:
1匹を空きスペースに移動させておき、残りのカエルの位置を入れ替える。
手数:
4匹の移動は、8手
2匹の移動は、3手
以上を3グループそれぞれですると、合わせて19手
【問題1−c】 150度回転
( 6)→(12)→(10)→( 4)→( 5)→( 2)→( 8)→( 2)→(12)→( 9)→ ( 4)→( 5)→( 1)→( 8)→( 3)→(10)→( 9)→( 7)→( 2)→( 3)→ ( 9)→( 6)→( 9)→(11)→( 6)→( 7)→( 1)→(11)→( 9)→手数:29手
◆香川県 fujita さんからの解答
【問題1】
●問題1−a 180度回転図
四角形3つについて考える。
基本図における
(1)1−4−7−10の四角形
(2)2−5−8−11の四角形
(3)3−6−9−12の四角形
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→( 4)→
//(1)を180度回転
( 2)→( 5)→( 8)→(11)→( 5)→( 8)→(11)→( 2)→
//(2)を180度回転
( 6)→( 3)→(12)→( 9)→( 3)→(12)→( 9)→( 6)→
//(3)を180度回転
よって、手数24回、手順は
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→( 4)→( 2)→( 5)→ ( 8)→(11)→( 5)→( 8)→(11)→( 2)→( 6)→( 3)→(12)→( 9)→ ( 3)→(12)→( 9)→( 6)→となる。
●問題1−b 左右反転図
それぞれの列について考える。
基本図における
(1)1の列
(2)3-2-12-11の列
(3)4-*-10の列
(4)5-6-8-9の列
(5)7の列
(1)(5)は考える必要がない。
( 2)→(11)→(12)→( 3)→(11)→(12)→( 3)→( 2)→
//(2)を左右反転させる
( 4)→(10)→( 4)→
//(3)を左右反転させる
( 8)→( 5)→( 6)→( 9)→( 5)→( 6)→( 9)→( 8)→
//(4)を左右反転させる
よって、手数19回、手順は
( 2)→(11)→(12)→( 3)→(11)→(12)→( 3)→( 2)→( 4)→(10)→ ( 4)→( 8)→( 5)→( 6)→( 9)→( 5)→( 6)→( 9)→( 8)→となる。
●問題1−c 150度回転図
30度反対にまわしてから、180度回転させる。
(12)→( 1)→( 2)→( 3)→( 4)→( 5)→( 6)→( 7)→ ( 8)→( 9)→(10)→(12)→( 1)→(11)→(12)→(11)→//30度回転させる
( 4)→( 7)→(10)→( 4)→( 7)→(10)→( 1)→//1-4-7-10の四角形を180度回転
( 5)→( 2)→(11)→( 8)→( 2)→(11)→( 8)→( 5)→//2-5-8-11の四角形を180度回転
( 3)→( 6)→( 9)→(12)→( 6)→( 9)→(12)→( 3)→//3-6-9-12の四角形を180度回転
よって、手数は39回、手順は
(12)→( 1)→( 2)→( 3)→( 4)→( 5)→( 6)→( 7)→( 8)→( 9)→ (10)→(12)→( 1)→(11)→(12)→(11)→( 4)→( 7)→(10)→( 4)→ ( 7)→(10)→( 1)→( 5)→( 2)→(11)→( 8)→( 2)→(11)→( 8)→ ( 5)→( 3)→( 6)→( 9)→(12)→( 6)→( 9)→(12)→( 3)→となる。
【問題2】
基本図において、1がそこ以外のどの場所とも交換できることを示せば、どの場所もほかのどの場所とでも交換できることが証明できる。
1において考える。
2と交換するには、
(12)→( 2)→( 1)→( 2)→(12)→
とすれば交換できる。
同様に12についても交換可能。
3と交換するには、
( 2)→( 3)→( 4)→( 1)→( 3)→( 4)→( 1)→( 4)→( 2)→
とすれば交換できる。
同様に11についても交換可能。
4と交換するには、
( 2)→( 4)→( 1)→( 4)→( 2)→
とすれば交換できる。
同様に10についても交換可能。
5と交換するには、
( 2)→( 5)→( 4)→( 1)→( 5)→( 4)→( 1)→( 4)→( 2)→
とすれば交換できる。
同様に9についても交換可能。
6と交換するには、
(12)→( 6)→( 4)→( 1)→( 6)→(12)→( 4)→( 1)→( 4)→
とすれば交換できる。
同様に8についても交換可能。
7と交換するには、
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→(10)→( 4)→
とすれば交換できる。
*と交換するには、
( 2)→( 1)→(12)→( 2)→( 1)→( 2)→(12)→
とすれば交換できる。
よって、1はどの場所とも交換することができる。
これによって、すべての場所は、ほかのどの場所とも交換することが可能である。
すなわち、どのようなカエルの配置に対しても、基本図から移動する手順は存在する。
◆東京都 明 さんからの解答
【問題1】
●問題1−a
手数 24手
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→( 4)→( 2)→(11)→ ( 8)→( 5)→(11)→( 8)→( 5)→( 2)→(12)→( 9)→( 6)→( 3)→ ( 9)→( 6)→( 3)→(12)●問題1−b
手数 19手
( 4)→(10)→( 4)→( 6)→( 9)→( 8)→( 5)→( 9)→( 8)→( 5)→ ( 6)→( 2)→(11)→(12)→( 3)→(11)→(12)→( 3)→( 2)●問題1−c
手数 27手
( 4)→( 2)→(12)→(10)→( 8)→( 6)→( 7)→( 2)→( 5)→(12)→ ( 3)→(10)→( 1)→( 8)→(11)→( 6)→( 4)→( 7)→( 1)→( 9)→ ( 4)→( 3)→( 9)→( 7)→(11)→( 5)→(11)最短手数を求めるための、実際に計算可能なアルゴリズムは解りませんでした。
【問題2】
任意の配置へ移動することができます。
【証明】
まず任意の隣合う蛙同士の置換が可能(他の位置に影響を与えず入れ替えができる)であることが判ります。
(隣合うケースは図形の対称性から基本的には(2)と(4)の関係と(1)と(2)の関係の2つのみで、置換が可能なことが明らかです。)
次に、隣合う蛙同士の置換により、離れた蛙同士の置換ができることを以下のように示すことができます。
任意の離れた蛙AとBの間に、隣同士で連絡する蛙a,b,cがあったとして、
A-a-b-c-Bの関係にあるとき、Aから順に隣同士の置換を行うことにより
a-b-c-B-Aとすることができます。
次にAは除いて、Bから順に隣同士の置換を行うとB-a-b-c-Aとなります。
以上により、他の位置に影響を与えず任意の2つの蛙を入れ替えができることが判ります。
基本図から、適当な蛙の置換を繰り返すことで、任意の蛙の配置へ変化させることができます。
なお、隣同士の蛙の置換は「ルール1」のみで可能ですので、任意配置への変更も「ルール1」のみでできることが判ります。
【おまけ】
最短手数が求められませんので解りませんでした。
ひとつの候補として、次のようなものを考えて見ました。
この場合は27手と思います。
| 3 | ||||||||||||
| / | \ | |||||||||||
| 1 | 8 | 6 | 9 | |||||||||
| \ | / | \ | / | \ | / | |||||||
| 10 | ※ | 4 | ||||||||||
| / | \ | / | \ | / | \ | |||||||
| 7 | 12 | 2 | 11 | |||||||||
| \ | / | |||||||||||
| 5 |
( 4)→( 1)→( 2)→( 3)→( 1)→( 2)→( 3)→( 8)→( 5)→( 6)→ ( 7)→( 5)→( 6)→( 7)→(12)→( 9)→(10)→(11)→( 9)→(10)→ (11)→( 2)→( 8)→( 6)→(12)→(10)→( 4)なお、参考に上下反転図と150度回転図について考えて見た結果を報告します。
上下反転図 (25手)
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→(11)→( 8)→( 9)→ (12)→( 8)→( 9)→(12)→(11)→(10)→( 2)→( 5)→( 6)→( 3)→ ( 5)→( 6)→( 3)→( 2)→( 4)150度回転図(24手)
( 4)→( 1)→(12)→( 9)→( 8)→( 5)→( 1)→(12)→( 9)→( 8)→ ( 5)→( 4)→( 6)→( 3)→( 2)→(11)→(10)→( 7)→( 3)→( 2)→ (11)→(10)→( 7)→( 6)
◆愛知県 Y.M.Ojisan さんからの解答
【問題1-a】 24
( 4)→( 1)→(10)→( 7)→( 1)→(10)→( 7)→( 4)→( 6)→( 3)→ (12)→( 9)→( 3)→(12)→( 9)→( 6)→( 2)→(11)→( 8)→( 5)→ (11)→( 8)→( 5)→( 2)→【問題1-b】 19
(12)→( 3)→( 2)→(11)→( 3)→( 2)→(11)→(12)→( 6)→( 9)→ ( 8)→( 5)→( 9)→( 8)→( 5)→( 6)→( 4)→(10)→( 4)→【問題1−c】 27
( 6)→( 4)→(10)→( 8)→( 2)→(12)→( 1)→( 8)→( 9)→( 4)→ ( 3)→(10)→( 7)→( 2)→( 6)→( 7)→( 5)→(12)→(11)→( 6)→ ( 9)→( 5)→(11)→( 9)→( 3)→( 1)→( 7)→【問題2】
可能である。
証明は難しくないが、ここでは下記おまけの探索で全点確認したことを証明とする。
【おまけ】
PCで探索した結果、最長は27回である。
即ち、1−cが最長ケースの1つである。
探索方式の詳細は略すが、効率化の考え方を以下に示す。
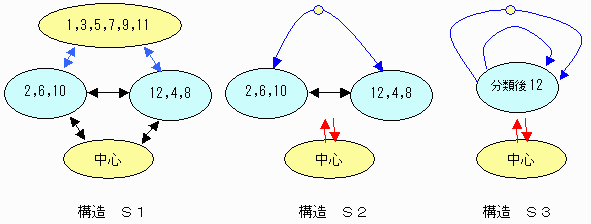
※の移動(矢印線)およびその位置に着目すると下記の構造S1があることがわかる。
なお、図中黒矢印は無条件、青矢印は条件付であることを表している。
中心および尖塔点を通過点とみなすと、さらにS2の構造とみなせる。
なお、図中赤矢印は特別な最初と最後の移動を示す。
また青矢印は1本で2手であり、複数の経路を代表。
さらに、回転6対称性と鏡像対称性で分類するとS3の構造にできる。
ただし、移動は1手と2手の2系統がある。
この分類により探索点の数は約5%に削減され、64Mのパソコンでもメモリ内に全ての点の探索状況を記憶することが可能になる。
後は、これを単純に初期位置から初めて絨毯爆撃(探索)することにより最も遠い前線上のS3による分類点を得ることができる。
最後に中央に※を移動して(+1手)解答が得られる。
なお、全く到達できない分類点は無かった。

【感想】
1-a,1-b は人間技で容易にできましたが、1-cは35回が限界でした。
PCで調べると意外に少なく、かつそれが最長だったので感心しました。
◆ 問題へもどる
◆ 今週の問題へ