◆埼玉県 i_masaru2002 さんからの解答
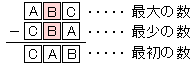
【問題1】 a≦b≦c (0≦a,b,c≦9) とおく。
c b a -) a b c ―――――――――― c-a-1 9 10-c+a9より大きな数は無いので、最大の数cは9をとることになる。
また、1+aはaとは異なるので、
c-a-1 = 8-a = a,
10-c+a = 1+a = b.
を得る。
式を解けば、a=4, b=5 を得る。
∴ (a, c, b) = (4, 9, 5).
【問題2】
a≦b≦c≦d (0≦a,b,c,d≦9) とおく。
d c b a -) a b c d ―――――――――――――― d-a c-b-1 9-(c-b) 10-(d-a)まず下記不等式が成り立つことが解る。
d-a≦c
c-b-1≦b
9-(c-b)≧b
10-(d-a)≧b
場合分けをして考える。
i) d-a=a と仮定した場合.
c-b-1=b ⇒ c=2b+1.
a < b < 2b+1 < 2a
これは矛盾である。
(d-a=a か c-b-1=a かのどちらかしかないので)
∴ c-b-1=a.
ii) d-a=b と仮定した場合
d-a=b ⇒ d-(c-b-1)=b ⇒ d+1=c
これは矛盾である。
∴ d-a=c
iii) 9-(c-b)=b と仮定した場合
c=9 ⇒ d=9.
10-(d-a)=d ⇒ 1+a=9 ⇒ a=8 ⇒ b=9-8=1 (<a).
これは矛盾である。
∴ 9-(c-b)=9-(a+1)=8-a=d.
10-(d-a)=10-c=b.
従って、下記の等式(必要十分条件)を得る。
a+b-c =-1 a +c-d=0 a +d=8 +b+c =10この解は、(a, b, c, d)=(1, 4, 6, 7)である。
∴ (c, a, d, b)=(6, 1, 7, 4).
◆千葉県 菜花子 さんからの解答
【問題1】 3桁

A>Cなので、C−Aは繰り下がりがある。
その場合(B−1)−Bは必ず9になる。
A−1−C=Cであるから
A=9とすると2C+1=9、C=4
10+C−A=Bであるから
B=14−9=5
したがってA=9,B=5,C=4
954 −459 ――――― 4953桁の「高橋の数」は495
【問題2】 4桁

3桁の場合、あいだに挟まれた数(B,B)の和は10になるので
4桁の場合も同様に(B,C)の和は10とすると、
A>Dなので、B+C=10となるBとCの数の組み合わせのうち、
(B−1)−C=Dの条件に合うのはB>Cの場合だけ。
B=6,C=4とすると、
6−1−4=D、D=1
A−D=Bなので、
A=B+D=6+1=7
したがってA=7,B=6,C=4,D=1
7641 −1467 ――――― 61747≦B≦9の場合は条件に合わないので解は一つ。
4桁の「高橋の数」は6174
【問題3】 4桁
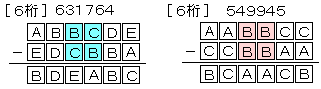
3桁、4桁の場合と同様に考えると、6桁以降は次の通り。
(5桁と7桁の場合はなし)
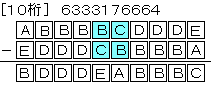
【問題4】
「高橋の数」はすべて9の倍数
「高橋の数」の並び方には規則性がある
◆広島県 清川 育男 さんからの解答
【問題1】
3桁 495=954-459
【問題2】
4桁 6174=7641-1467
【問題3】
5桁 なし
6桁
549945=995544-445599
631764=766431-134667
7桁 なし
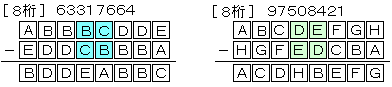
8桁
63317664=76664331-13346667
97508421=98754210-01245789
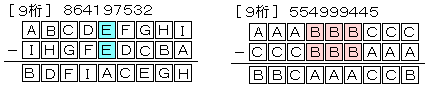
9桁
554999445=999555444-444555999
864197532=987654321-123456789
10桁
6333176664=7666643331-1333466667
9753086421=9876543210-0123456789
9975084201=9987542100-0012457899
11桁
86431976532=98766543321-12334566789
12桁
555499994445=999955554444-444455559999
633331766664=766666433331-133334666667
975330866421=987665433210-012334566789
997530864201=998765432100-001234567899
999750842001=999875421000-000124578999
13桁
8643319766532=9876665433321-1233345666789
【問題4】
9の倍数が必要条件。
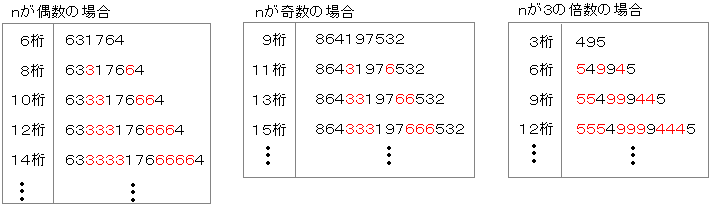
4桁以上の偶数桁では「高橋の数」が必ず存在する。
6174=7641-1467 631764=766431-134667 63317664=76664331-13346667 6333176664=7666643331-1333466667 633331766664=766666433331-133334666667 .......................................
9以上の奇数桁「高橋の数」
9 864197532=987654321-123456789 11 86431976532=98766543321-12334566789 13 8643319766532=9876665433321-1233345666789 15 864333197666532=987666654333321-123333456666789 ...................................................
3nの「高橋数」
3 495=954-459 6 549945=995544-445599 9 554999445=999555444-444555999 12 555499994445=999955554444-444455559999 15 555549999944445=999995555544444-444445555599999 ....................................................
8 97508421=98754210-01245789 10 9753086421=9876543210-0123456789 12 975330866421=987665433210-012334566789 14 97533308666421=98766654333210-01233345666789 ............................................... 2n+61,2,5,7 は存在しない。
循環しない最初の1個をみつければよいことになる。
1) 3 495=954-459 6 549945=995544-445599 9 554999445=999555444-444555999 12 555499994445=999955554444-444455559999 15 555549999944445=999995555544444-444445555599999 2) 4 6174=7641-1467 6 631764=766431-134667 8 63317664=76664331-13346667 10 6333176664=7666643331-1333466667 12 633331766664=766666433331-133334666667 14 63333317666664=76666664333331-13333346666667 3) 8 97508421=98754210-01245789 10 9975084201=9987542100-0012457899 12 999750842001=999875421000-000124578999 14 99997508420001=99998754210000-00001245789999 4) 9 864197532=987654321-123456789 11 86431976532=98766543321-12334566789 13 8643319766532=9876665433321-1233345666789 15 864333197666532=987666654333321-123333456666789 5) 10 9753086421=9876543210-0123456789 12 975330866421=987665433210-012334566789 14 97533308666421=98766654333210-01233345666789 6) 10 9753086421=9876543210-0123456789 12 997530864201=998765432100-001234567899 14 99975308642001=99987654321000-00012345678999「6系列」以外の存在が疑問として残ります。
【おまけ】
3桁 495=954-459 4桁 6174=7641-1467 6桁 549945=995544-445599 631764=766431-134667 660852=866520-205668 * 8桁 63317664=76664331-13346667 66308652=86665320-20356668 * 9桁 554999445=999555444-444555999 864197532=987654321-123456789 10桁 6333176664=7666643331-1333466667 6633086652=8666653320-2033566668 * 6752087442=8776544220-2024456778*印には規則性があります。
6 660852=866520-205668 8 66308652=86665320-20356668 10 6633086652=8666653320-2033566668 12 663330866652=866666533320-203335666668 14 66333308666652=86666665333320-20333356666668 16 6633333086666652=8666666653333320-2033333566666668nは自然数
| A(3n)=5* | 10N-1 9 |
*(102*N-1) |
| A(2n+2)=6*102*N+1+3* | 10N-1-1 9 |
*10N+2+17*10N+6* | 10N-1-1 9 |
*10+4 |
| A(2n+4)=66*102*N+2+3* | 10N-1-1 9 |
*10N+3+8*10N+1+6* | 10N-1-1 9 |
*102+52 |
| A(2n+7)=864*102*N+4+3* | 10N-1-1 9 |
*10N+5+197*10N+2+6* | 10N-1-1 9 |
*103+532 |
| A(2n+8)=675*102*N+5+3* | 10N-1-1 9 |
*10N+6+2087*10N+2+6* | 10N-1-1 9 |
*103+442 |
?
◆東京都 明 さんからの解答
【問題1】
3桁の各桁の数字をa,b,cとし、a≧b≧cとします。
a=cでは3つの数字でできる最大値−最小値は0となるため不適。
よって、a>cであり、最大値−最小値の各桁は、
一位の桁は 10-(a-c)
十位の桁は b-b-1+10=9
百位の桁は a-c-1
となります。
十位の桁に9があることから、a=9
したがって、
一位の桁は1+c
百位の桁は8-c
となります。
いずれかの桁がcとなりますが、一位の桁がcにならないことは明らか。
よって、8-c=cであり、c=4となります。
残りの一位の桁は5となり、これが残りのbの数字となります。
以上より、最大値は954、最小値は459で、差は495となり、この数字は間違いなくa,b,cで構成されています。
したがって、3桁の「高橋の数」は495であり、この数字に限ります。
答え 495
【問題2】【問題3】
【問題2】も【問題1】と同様な方法で解けますが、1本道ではなく、場合分けが必要になってきます。
【問題2】に計算機を持ち出すのはは不適当ですが、【問題3】と合わせて20桁まで計算機で求めた解として下記に表記します。
桁数 : 4 高橋数 : 6174 MAX : 7641 MIN : 1467 桁数 : 5 解なし 桁数 : 6 高橋数 : 631764 MAX : 766431 MIN : 134667 高橋数 : 549945 MAX : 995544 MIN : 445599 桁数 : 7 解なし 桁数 : 8 高橋数 : 97508421 MAX : 98754210 MIN : 1245789 高橋数 : 63317664 MAX : 76664331 MIN : 13346667 桁数 : 9 高橋数 : 864197532 MAX : 987654321 MIN : 123456789 高橋数 : 554999445 MAX : 999555444 MIN : 444555999 桁数 : 10 高橋数 : 9975084201 MAX : 9987542100 MIN : 12457899 高橋数 : 9753086421 MAX : 9876543210 MIN : 123456789 高橋数 : 6333176664 MAX : 7666643331 MIN : 1333466667 桁数 : 11 高橋数 : 86431976532 MAX : 98766543321 MIN : 12334566789 桁数 : 12 高橋数 : 999750842001 MAX : 999875421000 MIN : 124578999 高橋数 : 997530864201 MAX : 998765432100 MIN : 1234567899 高橋数 : 975330866421 MAX : 987665433210 MIN : 12334566789 高橋数 : 633331766664 MAX : 766666433331 MIN : 133334666667 高橋数 : 555499994445 MAX : 999955554444 MIN : 444455559999 桁数 : 13 高橋数 : 8643319766532 MAX : 9876665433321 MIN : 1233345666789 桁数 : 14 高橋数 : 99997508420001 MAX : 99998754210000 MIN : 1245789999 高橋数 : 99975308642001 MAX : 99987654321000 MIN : 12345678999 高橋数 : 99753308664201 MAX : 99876654332100 MIN : 123345667899 高橋数 : 97755108844221 MAX : 98877554422110 MIN : 1122445577889 高橋数 : 97533308666421 MAX : 98766654333210 MIN : 1233345666789 高橋数 : 63333317666664 MAX : 76666664333331 MIN : 13333346666667 桁数 : 15 高橋数 : 864333197666532 MAX : 987666654333321 MIN : 123333456666789 高橋数 : 555549999944445 MAX : 999995555544444 MIN : 444445555599999 桁数 : 16 高橋数 : 9999975084200001 MAX : 9999987542100000 MIN : 12457899999 高橋数 : 9999753086420001 MAX : 9999876543210000 MIN : 123456789999 高橋数 : 9997533086642001 MAX : 9998766543321000 MIN : 1233456678999 高橋数 : 9977551088442201 MAX : 9988775544221100 MIN : 11224455778899 高橋数 : 9975333086664201 MAX : 9987666543332100 MIN : 12333456667899 高橋数 : 9775531088644221 MAX : 9887765544322110 MIN : 112234455677889 高橋数 : 9753333086666421 MAX : 9876666543333210 MIN : 123333456666789 高橋数 : 6333333176666664 MAX : 7666666643333331 MIN : 1333333466666667 桁数 : 17 高橋数 : 98765420987543211 MAX : 99887765544322110 MIN : 1122344556778899 高橋数 : 86433331976666532 MAX : 98766666543333321 MIN : 12333334566666789 桁数 : 18 高橋数 : 999999750842000001 MAX : 999999875421000000 MIN : 124578999999 高橋数 : 999997530864200001 MAX : 999998765432100000 MIN : 1234567899999 高橋数 : 999975330866420001 MAX : 999987665433210000 MIN : 12334566789999 高橋数 : 999775510884422001 MAX : 999887755442211000 MIN : 112244557788999 高橋数 : 999753330866642001 MAX : 999876665433321000 MIN : 123334566678999 高橋数 : 997755310886442201 MAX : 998877655443221100 MIN : 1122344556778899 高橋数 : 997533330866664201 MAX : 998766665433332100 MIN : 1233334566667899 高橋数 : 977553310886644221 MAX : 988776655443322110 MIN : 11223344556677889 高橋数 : 975333330866666421 MAX : 987666665433333210 MIN : 12333334566666789 高橋数 : 886644219977553312 MAX : 998877665544332211 MIN : 112233445566778899 高橋数 : 633333331766666664 MAX : 766666666433333331 MIN : 133333334666666667 高橋数 : 555554999999444445 MAX : 999999555555444444 MIN : 444444555555999999 桁数 : 19 高橋数 : 9987654209875432101 MAX : 9998877655443221100 MIN : 11223445567788999 高橋数 : 9876543209876543211 MAX : 9988776655443322110 MIN : 112233445566778899 高橋数 : 8643333319766666532 MAX : 9876666665433333321 MIN : 1233333345666666789 桁数 : 20 高橋数 : 99999997508420000001 MAX : 99999998754210000000 MIN : 1245789999999 高橋数 : 99999975308642000001 MAX : 99999987654321000000 MIN : 12345678999999 高橋数 : 99999753308664200001 MAX : 99999876654332100000 MIN : 123345667899999 高橋数 : 99997755108844220001 MAX : 99998877554422110000 MIN : 1122445577889999 高橋数 : 99997533308666420001 MAX : 99998766654333210000 MIN : 1233345666789999 高橋数 : 99977553108864422001 MAX : 99988776554432211000 MIN : 11223445567788999 高橋数 : 99975333308666642001 MAX : 99987666654333321000 MIN : 12333345666678999 高橋数 : 99775533108866442201 MAX : 99887766554433221100 MIN : 112233445566778899 高橋数 : 99753333308666664201 MAX : 99876666654333332100 MIN : 123333345666667899 高橋数 : 97775551108884442221 MAX : 98887775554442221110 MIN : 1112224445557778889 高橋数 : 97755333108866644221 MAX : 98877666554433322110 MIN : 1122333445566677889 高橋数 : 97533333308666666421 MAX : 98766666654333333210 MIN : 1233333345666666789 高橋数 : 88664432199776553312 MAX : 99887766655443332211 MIN : 11223334455666778899 高橋数 : 63333333317666666664 MAX : 76666666664333333331 MIN : 13333333346666666667【問題4】
【問題3】の結果から、「高橋の数」には下記の特徴が見えます。
最大値に着目すると、基本的な解954、7641と、これから帰納法的に導くことができる、
995544、999555444、766431、76664331に分けられそうです。
基本解と見られるものは上記の中では以下になると思います。
954、7641、98754210、987654321
他の解は基本解から帰納法的に桁数を拡大して導くことができます。
桁数の増加にともない基本解がどのように増加していくのかは考察できていません。
【おまけ】
同じプログラムでの12桁までの計算機解を以下に表記します。
桁数 : 3 高橋数 : 495 MAX : 954 MIN : 459 桁数 : 4 高橋数 : 6174 MAX : 7641 MIN : 1467 桁数 : 5 解なし 桁数 : 6 高橋数 : 660852 MAX : 866520 MIN : 205668 高橋数 : 631764 MAX : 766431 MIN : 134667 高橋数 : 549945 MAX : 995544 MIN : 445599 桁数 : 7 解なし 桁数 : 8 高橋数 : 66308652 MAX : 86665320 MIN : 20356668 高橋数 : 63317664 MAX : 76664331 MIN : 13346667 桁数 : 9 高橋数 : 864197532 MAX : 987654321 MIN : 123456789 高橋数 : 554999445 MAX : 999555444 MIN : 444555999 桁数 : 10 高橋数 : 6752087442 MAX : 8776544220 MIN : 2024456778 高橋数 : 6633086652 MAX : 8666653320 MIN : 2033566668 高橋数 : 6333176664 MAX : 7666643331 MIN : 1333466667 桁数 : 11 高橋数 : 86431976532 MAX : 98766543321 MIN : 12334566789 桁数 : 12 高橋数 : 675320876442 MAX : 877665443220 MIN : 202344566778 高橋数 : 663330866652 MAX : 866666533320 MIN : 203335666668 高橋数 : 633331766664 MAX : 766666433331 MIN : 133334666667 高橋数 : 555499994445 MAX : 999955554444 MIN : 444455559999
題意に添って「数字が高橋数か」でプログラムを組むと効率が悪いと気が付きましたので、「最大値で作られる数が高橋数となるか」に
作り直しました。
(10進BASICです。)
LET MXF=12
DIM COL(MXF)
DIM CLN(MXF)
DIM WRK(MXF)
FOR FIG=3 TO MXF
PRINT "桁数 : ";FIG
LET EXT=0
MAT COL=ZER
DO
CALL coutup(FIG,COL,EDM)
LET MX=0
FOR J=1 TO FIG
LET MX=10*MX
LET MX=MX+COL(J)
NEXT J
CALL sermin(FIG,COL,MN)
LET N=MX-MN
CALL looknm(N,CLN)
CALL sermax(FIG,CLN,ANS)
IF ANS=MX AND INT(N/10^(FIG-1))>0 THEN
PRINT "高橋数 : ";N
PRINT "MAX : ";MX;" MIN : ";MN
PRINT
LET EXT=1
END IF
LOOP UNTIL EDM=1
IF EXT=0 THEN
PRINT"解なし"
PRINT
END IF
NEXT FIG
PRINT "終了"
SUB coutup(DIM,ARR(),EDM)
LET EDM=0
LET cuC=1
IF ARR(cuC)<9 THEN
LET ARR(cuC)=ARR(cuC)+1
ELSE
DO
LET cuC=cuC+1
IF cuC>DIM THEN
LET EDM=1
EXIT DO
ELSEIF ARR(cuC)<9 THEN
LET cuN=ARR(cuC)+1
FOR cuJ=cuC TO 1 STEP -1
LET ARR(cuJ)=cuN
NEXT cuJ
EXIT DO
END IF
LOOP
END IF
END SUB
SUB looknm(N,ARR())
MAT ARR=ZER
LET lnN=N
LET lnJ=0
DO
LET lnJ=lnJ+1
LET ARR(lnJ)=MOD(lnN,10)
LET lnN=INT(lnN/10)
LOOP UNTIL lnN=0
END SUB
SUB sermax(DIM,ARR(),N)
MAT WRK=ARR
LET N=0
FOR sxJ=1 TO DIM
LET N=10*N
LET sxN=-1
FOR sxK=1 TO DIM
IF sxN<WRK(sxK) THEN
LET sxN=WRK(sxK)
LET sxM=sxK
END IF
NEXT sxK
LET WRK(sxM)=-1
LET N=N+sxN
NEXT sxJ
END SUB
SUB sermin(DIM,ARR(),N)
MAT WRK=ARR
LET N=0
LET snJ=1
LET snN=10
FOR snK=1 TO DIM
IF snN>WRK(snK) AND WRK(snK)<>0 THEN
REM "AND WRK(snK)<>0"を外すとMIN数の最上位に0を許す
LET snN=WRK(snK)
LET snM=snK
END IF
NEXT snK
LET WRK(snM)=10
LET N=N+snN
FOR snJ=2 TO DIM
LET N=10*N
LET snN=10
FOR snK=1 TO DIM
IF snN>WRK(snK) THEN
LET snN=WRK(snK)
LET snM=snK
END IF
NEXT snK
LET WRK(snM)=10
LET N=N+snN
NEXT snJ
END SUB
END
◆愛知県 Y.M.Ojisan さんからの解答
全般に10進数を [A,B,C]=100A+10B+C と表すこととします。
【問題1】 495
3桁の数を[α,β,γ]とし 最大数を[a,b,c] 最小数を[c,b,a]とします。このとき
[a,b,c]−[c,b,a]=[a,0,c]−[c,0,a]=99(a-c)=[α,9,γ]=[b,9,c] or[c,9,b]
です。a=9は決定です。
整理すると 801=100(b+c) or 801=199c+b です。
前者は成立しません。
後者はc=4、b=5のみです。
【問題2】 6174
4桁の数を[α,β,γ,δ]とし 最大数を[a,b,c,d] 最小数を[d,c,b,a]とします。このとき
[a,b,c,d]−[d,c,b,a]=999(a-d)+90(b-c) です。
X=a-d, Y=b-c とおけば
[α,β,γ,δ]=999X+90Y 9≧X≧Y≧0 とおけることが判ります。
Y=0の場合 999X=[X-1,9,9,10−X] なのでa=b=c=9 が定まり、適当なXがありません。
よって 9≧X≧Y≧1です。
この45通りを調べると、解が得られます。
【問題3】
下表にPCでの計算結果(3〜23桁)を示します。
5桁と7桁は存在しません。
【問題4】
8桁以上は必ず存在する。下表最下3行参照。
【おまけ】
下表に示す。16桁以上で必ず存在する。
奇数桁のときは中央に9が必ず存在するので、1が存在する。
偶数桁のときは中央2桁に注目することにより、1ないし2が存在することが証明できる。
これらを利用して探索を効率化した。
| 高橋数/おまけ数 | 高橋数 | おまけ数 | |
| 桁数 | 0を含まない | 0を含む | 0を含む |
| 3 | 495 | - | - |
| 4 | 6174 | - | - |
| 5 | - | - | - |
| 6 | 549945 631764 |
- | 660852 |
| 7 | - | - | - |
| 8 | 63317664 | 97508421 | 66308652 |
| 9 | 554999445 864197532 |
- | - |
| 10 | 6333176664 | 9753086421 9975084201 |
6633086652 6752087442 |
| 11 | 86431976532 | - | - |
| 12 | 555499994445 633331766664 |
975330866421 997530864201 999750842001 |
663330866652 675320876442 |
| 13 | 8643319766532 | - | - |
| 14 | 63333317666664 | 97533308666421 97755108844221 99753308664201 99975308642001 99997508420001 |
66333308666652 67533208766442 |
| 15 | 555549999944445 864333197666532 |
- | - |
| 16 | 6333333176666664 | 9753333086666421 9775531088644221 9975333086664201 9977551088442201 9997533086642001 9999753086420001 9999975084200001 |
6633333086666652 6753332087666442 |
| 17 | 86433331976666532 | 98765420987543211 | 89765420987543211 |
| 18 | 555554999999444445 633333331766666664 886644219977553312 |
975333330866666421 977553310886644221 997533330866664201 997755310886442201 999753330866642001 999775510884422001 999975330866420001 999997530864200001 999999750842000001 |
663333330866666652 675333320876666442 |
| 19 | 8643333319766666532 | 9876543209876543211 9987654209875432101 |
8976543209876543211 |
| 20 | 63333333317666666664 88664432199776553312 |
97533333308666666421 97755333108866644221 97775551108884442221 99753333308666664201 99775533108866442201 99975333308666642001 99977553108864422001 99997533308666420001 99997755108844220001 99999753308664200001 99999975308642000001 99999997508420000001 |
66333333308666666652 67533333208766666442 |
| 21 | 555555499999994444445 864333333197666666532 |
987654332098766543211 998765432098765432101 999876542098754321001 |
897654332098766543211 899765432098765432101 899976542098754321001 |
| 22 |
6333333333176666666664 8866443321997766553312 |
9753333333086666666421 9775533331088666644221 9777555311088864442221 9975333333086666664201 9977553331088666442201 9977755511088844422201 9997533333086666642001 9997755331088664422001 9999753333086666420001 9999775531088644220001 9999975333086664200001 9999977551088442200001 9999997533086642000001 9999999753086420000001 9999999975084200000001 |
6633333333086666666652 6753333332087666666442 |
| 23 | 86433333331976666666532 87765443219997765543222 |
98765433320987666543211 98776554210988754432211 99876543320987665432101 99987654320987654321001 99998765420987543210001 |
89765433320987666543211 89776554210988754432211 89976543320987665432101 89997654320987654321001 89999765420987543210001 |
| 偶数桁例 | 633〜331766〜664 | 97533〜330866〜66421 999〜9975084200〜001 |
6633〜330866〜6652 6753〜320876〜6442 |
| 奇数桁例 | 86433〜3319766〜66532 | 9876543〜332098766〜6543211 99〜998765420987543210〜001 |
8976543〜33209876〜66543211 89〜999765420987543210〜001 |
| 3の倍数桁例 | 55〜55499〜99944〜445 | - | - |
注記) xx〜xxは 同じ桁数(0〜)の数字を入れます。
【PS】
あまり良い結果は出せませんでした。
そこで、多数の結果を示し、どなたかのひらめきを期待します。
◆ 問題へもどる
◆ 今週の問題へ